Calculating the diagonal of a square and rectangle shape

You're in need of calculating the diagonal of a square, or the diagonal of a rectangle but somehow you've forgotten the method. Let's refresh your memory with the following article on how to calculate the diagonal of a square, or a rectangle.

Below, you'll find the method for calculating the diagonal of a square, and also the method for calculating the diagonal of a rectangle. Let's dive in.

Calculating the diagonal of a square

In Euclidean geometry, a square is a regular quadrilateral. A square can be considered as a rectangle with equal sides, or as a rhombus with two equal diagonals.

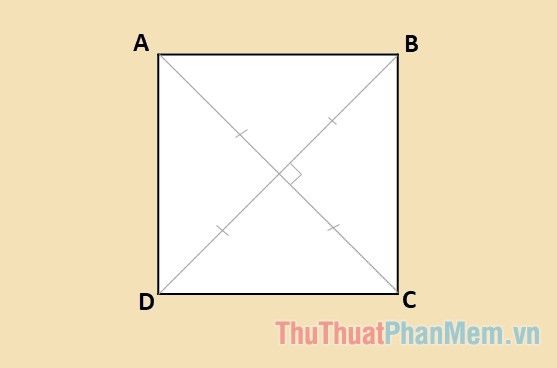
Properties of a square

• In a square, both diagonals are equal, perpendicular, and intersect at the midpoint of each diagonal.
• There exists both an inscribed and circumscribed circle, with the center of both circles coinciding and being the intersection point of the two diagonals of the square.
• One diagonal divides the square into two equal areas.
• The bisectors of the angles, medians, and perpendicular bisectors all intersect at a single point.
• A square possesses all the properties of a rectangle, parallelogram, and rhombus.

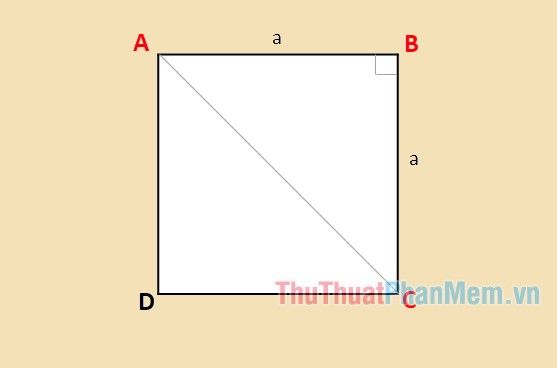
Method for calculating the diagonal of a square

According to the properties of a square, the diagonals of a square are equal, and one diagonal divides the square into two equal parts, forming two right isosceles triangles. Therefore, the diagonal of a square is the hypotenuse of these two triangles. To calculate the diagonal of a square, you simply apply the Pythagorean theorem to the right isosceles triangles.

Suppose you have square ABCD with side length a, and diagonal AC divides the square into two right isosceles triangles ABC and ACD. Applying the Pythagorean theorem to right isosceles triangle ABC:

AC2=AB2+BC2$A{C}^2=A{B}^2+B{C}^2$

HayAC2=a2+a2=2aa2$\mathrm{H\; <div\; class="min-w-[250px]\; max-w-[94vw]\; md:max-w-[770px]">\; <ins\; class="adsbygoogle"\; style="display:block;\; text-align:center;"\; data-ad-layout="in-article"\; data-ad-format="fluid"\; data-ad-client="ca-pub-9247024304160346"\; data-ad-slot="4115752014"></ins>\; </div>}ayA{C}^2=a^2+a^2=2a^2$

⇒AC=a√2$\Rightarrow AC=a\sqrt{2}$

Therefore, the diagonal of a square with side length a is a√2$a\sqrt{2}$

Calculating the diagonal of a rectangle

In Euclidean geometry, a rectangle is a convex quadrilateral with four right angles. It is a parallelogram with two equal diagonals.

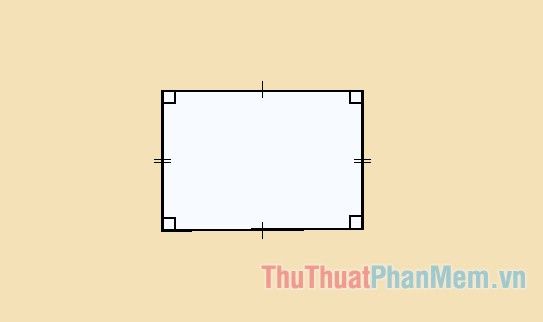
Properties of a rectangle

• In a rectangle, the diagonals are equal and intersect at the midpoint of each diagonal.
• A rectangle possesses all the properties of a trapezoid and parallelogram.
• The diagonals in a rectangle intersect to form 4 congruent triangles.

Method for calculating the diagonal of a rectangle

A rectangle has 4 equal right angles, its diagonals are equal, so one diagonal of the rectangle divides it into 2 right triangles, and the diagonal of the rectangle is the hypotenuse, while the two sides of the rectangle are the legs. To calculate the diagonal of a rectangle, you also use the Pythagorean theorem.

Suppose you have rectangle ABCD with length a and width b, diagonal AC as shown below:

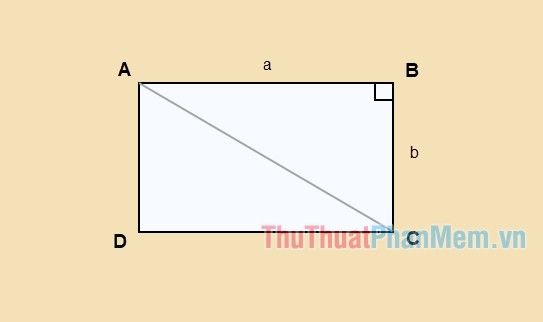
Applying the Pythagorean theorem to right triangle ABC:

AC2=AB2+BC2$A{C}^2=A{B}^2+B{C}^2$

⇔AC2=a2+b2$\iff A{C}^2=a^2+b^2$

⇔AC=√(a2+b2)$\iff AC=\sqrt{\left(a^2+b^2\right)}$

The diagonal of a rectangle with length a and width b is √(a2+b2)$\sqrt{\left(a^2+b^2\right)}$

This article has shared with you how to calculate the diagonal of a square and the diagonal of a rectangle. Whether you're calculating the diagonal of a square or rectangle, you just need to apply the Pythagorean theorem to easily find the diagonals. Wish you success!