Discover the secret to calculating the volume of a pyramid effortlessly and master the art of pyramid volume calculation.

Are you on a quest for the formula to compute the volume of a pyramid? Look no further! Dive into this article to unveil the formula and techniques for calculating pyramid volume.

Below lies the formula for finding the volume of a pyramid along with concrete examples illustrating the process. Join us as we delve into the realm of pyramid volume calculation.

Unraveling the Concept of Pyramids

• A pyramid features a polygonal base and triangular sides meeting at a common vertex, known as the apex of the pyramid.
• The line passing through the apex and perpendicular to the base plane is termed as the height of the pyramid.
• The nomenclature of a pyramid depends on its base polygon: a pyramid with a triangular base is called a triangular pyramid, while one with a quadrilateral base is termed as a quadrilateral pyramid.

Special Pyramidal Solids

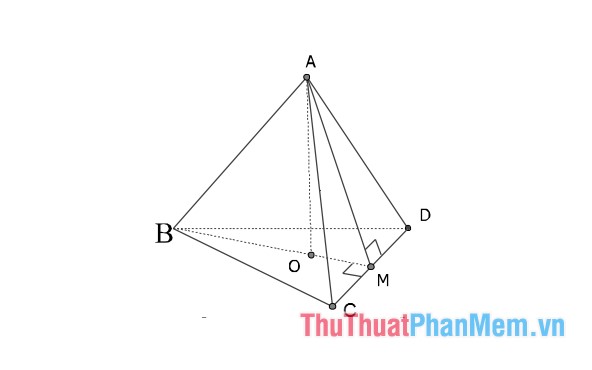
1. Regular Tetrahedral Pyramid

This pyramid possesses all equal edges, and all faces are equilateral triangles. O represents the centroid of the base triangle, and AO is perpendicular to (BCD).

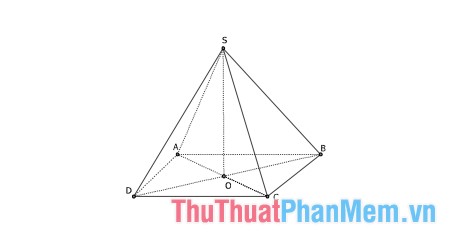
2. Regular Quadrilateral Pyramid

This pyramid has all equal lateral edges, with the base polygon being a square centered at O, where SO is perpendicular to (ABCD).

Formula for Calculating Pyramid Volume

The volume of a regular pyramid equals one-third of the base area multiplied by the height.

V=13S.h$V=\frac{1}{3}S.h$

Where:

• V represents the volume of the pyramid.
• S denotes the area of the pyramid's base.
• h signifies the height of the pyramid.
• The standard unit for volume measurement is cubic meters (m3$m^3$).

Example

Given the pyramid S.ABCD, where ABCD is a square base with side length a, and SA is perpendicular to the base plane with SC forming a 60o${60}^o$ angle with the base. Calculate the volume of pyramid S.ABCD.

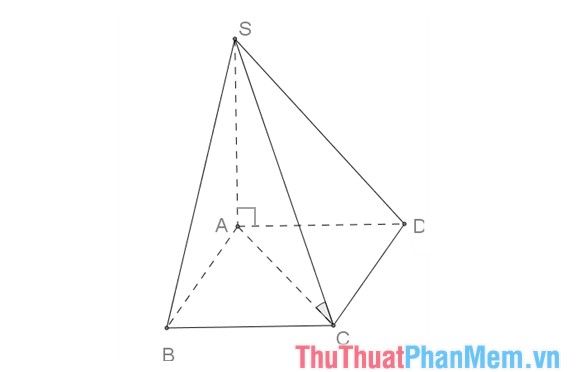
Solution:

According to the volume formula V=13S.h$V=\frac{1}{3}S.h$, you need to calculate the height and base area.

• Area of square ABCD: SABCD=a$S_{ABCD}=a$

• Calculate the height of the pyramid:

AC represents the projection of SC onto the plane (ABCD), thus:

(SC,(ABCD))=(SC,AC)=ˆSCA=45o$\left(SC,\left(ABCD\right)\right)=\left(SC,AC\right)=\widehat{SCA}={45}^o$

AC=a√2,SA=AC.tan60o=a√6$AC=a\sqrt{2},SA=AC.\tan {60}^o=a\sqrt{6}$

After calculating the area of square ABCD and the height of the pyramid, you will compute the Volume of the Pyramid:

V=13.a2.√6=a3√33$V=\frac{1}{3}.a^2.a\sqrt{6}=\frac{a^3\sqrt{3}}{3}$

So the volume of the pyramid S.ABCD is a3√33$\frac{a^3\sqrt{3}}{3}$

Above, the article has shared the formula for calculating the volume of a pyramid and an example of how to compute it. Hope this article will enhance your understanding and knowledge on calculating pyramid volumes. Wishing you success!