Formula for calculating the perimeter of a rhombus & illustrative examples

Calculating the perimeter of a rhombus is a common exercise encountered when studying plane geometry. If you're still unsure about how to calculate the perimeter of a rhombus and need to explore more to solve various perimeter-related problems, then let's delve into the Formula for calculating the perimeter of a rhombus & illustrative examples in the article below.

I. What is a rhombus? What is the perimeter of a rhombus?

A rhombus in Euclidean geometry is defined as a quadrilateral with four equal sides. A rhombus is also a parallelogram with two adjacent sides equal, or a parallelogram with two diagonals perpendicular to each other.

Perimeter of a rhombus is the boundary line surrounding the entire area of the shape, or simply put, the sum of the lengths of all the boundaries of the rhombus.

Properties of a rhombus

• Opposite angles are equal
• Two diagonals are perpendicular and intersect at the midpoint of each diagonal
• Diagonals are bisectors of the angles of the rhombus
• A rhombus possesses all the properties of a parallelogram

II. Formula for calculating the perimeter of a rhombus

The perimeter of a rhombus is the boundary line surrounding the entire area of the shape. To calculate the perimeter of a rhombus, simply add the total length of its 4 sides. Since all sides of a rhombus are equal, you just need to multiply the length of one side by 4 (4 represents the 4 sides of the rhombus).

Formula for calculating the perimeter of a rhombus: P = a x 4.

Where:

• P is the perimeter of the rhombus.
• a is the length of one side of the rhombus.

III. Illustrative Examples

Type 1: Calculating the perimeter of a rhombus when the length of a side is known

For this type of problem, you just need to apply the perimeter formula P = a x 4.

Example 1: Calculate the perimeter of a rhombus when the length of a side = 8 cm.

Solution: Applying the formula for calculating the perimeter of a rhombus P = a x 4

So the perimeter of the rhombus is: 8 x 4 = 32 cm.

Type 2: Calculating the perimeter of a rhombus given the lengths of the diagonals

The diagonals of a rhombus are perpendicular and intersect at the midpoint of each diagonal, so the diagonals divide the rhombus into 4 right triangles. Therefore, when you need to calculate the perimeter of a rhombus given the lengths of the diagonals, you need to apply the Pythagorean theorem in the right triangles to find the length of a side of the rhombus. Then apply the formula for calculating the perimeter of a rhombus to find the perimeter of the rhombus.

Example 2: Calculate the perimeter of a rhombus given the lengths of its diagonals are 12 cm and 16 cm.

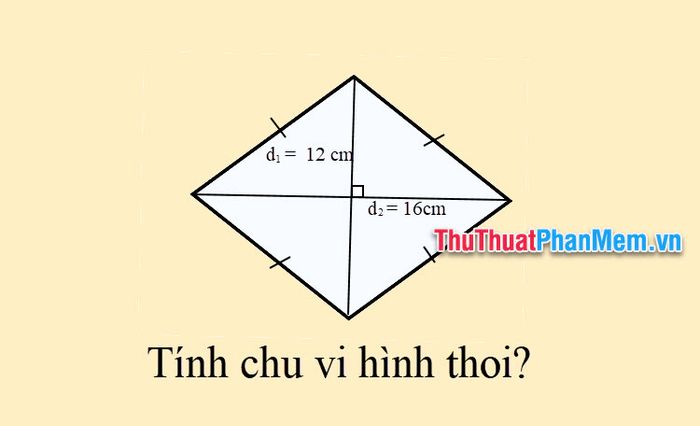
Solution: Let the side of the rhombus be denoted by a, and the diagonals of the rhombus be denoted as d1$d_1$ and d2$d_2$.

Applying the Pythagorean theorem in the right triangle, the square of the hypotenuse is equal to the sum of the squares of the two perpendicular sides.

Considering the right triangle with the hypotenuse as a, the two perpendicular sides as d12$\frac{d_1}{2}$ and d22$\frac{d_2}{2}$, we have:

a2=(d12)2+(d22)2=62+82=100$a^2={\left(\frac{d_1}{2}\right)}^2+{\left(\frac{d_2}{2}\right)}^2=6^2+8^2=100$

Therefore, a = 10 cm

The perimeter of the rhombus P = a x 4 = 10 x 4 = 40 cm

Therefore, the perimeter of the rhombus is 40 cm.

Here, Mytour has explored rhombuses with you, including the formula for calculating their perimeter and specific examples. We hope that after reviewing this article, you will have a better understanding of rhombuses and how to calculate their perimeters. You should practice various exercises on calculating rhombus perimeters to enhance your knowledge. Thank you for your interest and following this article.