Formula for Pyramid Surface Area & Illustrative Examples

To supplement missing knowledge, the aspects you may not understand about pyramids, the formulas for pyramid surface area are shared here. This article by Mytour presents you with formulas for calculating pyramid surface area & illustrative examples. Feel free to explore.

I. What is a Pyramid? What is an Equilateral Pyramid?

1. What is a Pyramid?

In spatial geometry, a pyramid is a polyhedron with a convex polygon base, triangular sides, and a common vertex – the apex. The apex is not located on the base.

There are various types of pyramids, named based on their base shapes. For instance, an equilateral triangular pyramid has an equilateral triangular base, a triangular pyramid has a triangular base, a quadrilateral pyramid has a quadrilateral base, a trapezoidal pyramid has a trapezoidal base, and so on.

2. Properties of Pyramids

• A line passing through the apex and perpendicular to the base is called the height of the pyramid.
• A pyramid with congruent lateral edges or congruent lateral faces has the height's foot as the center of the circumscribed circle of the base.
• If a pyramid's lateral face or slant height is perpendicular to the base, the height of the pyramid is the height of that lateral face or slant height.
• If the lateral faces align with the base such that the angles are equal or the height lines from the apex to the base are the same, the height's foot is the center of the inscribed circle of the base.

3. What is an Equilateral Pyramid?

In spatial geometry, an equilateral pyramid is a common and special form of pyramid where the base is an equilateral polygon, and the lateral faces are congruent triangles. Examples include the equilateral triangular pyramid, the equilateral quadrilateral pyramid, etc.

Properties of Equilateral Pyramid:

• The base of an equilateral pyramid is an equilateral polygon, such as a square, equilateral triangle, pentagon, etc.
• The center of the equilateral base coincides with the foot of the height of the equilateral pyramid.

II. Formula for Calculating Pyramid Surface Area

1. Formula for Calculating Lateral Surface Area of a Pyramid

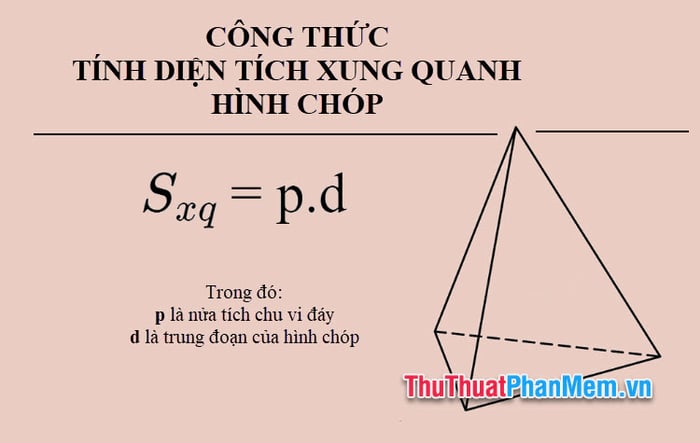
The lateral surface area of a pyramid is the sum of the areas of its lateral faces. To calculate the lateral surface area, we use the formula:

Sxq$S_{xq}$ = p.d

In which:

• Sxq$S_{xq}$ is the lateral surface area of the pyramid
• p is half the perimeter of the base
• d is the midsegment of the pyramid (the perpendicular from the apex to the midpoint of each edge of the base)

Note: The formula above applies only to pyramids with equilateral triangular lateral faces. For pyramids with different lateral faces, the area of each face needs to be calculated separately and summed to find the total lateral surface area.

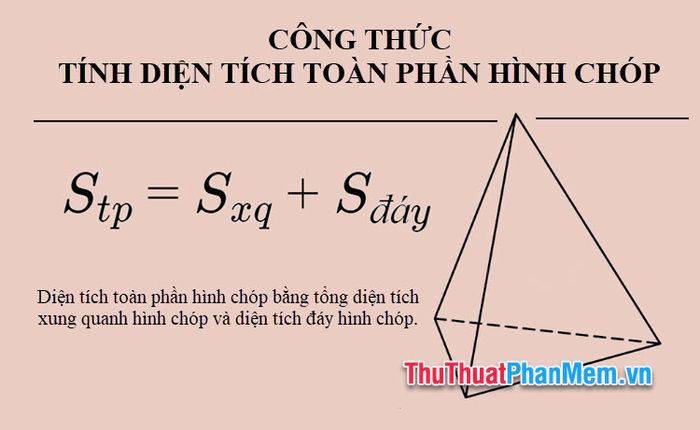
2. Formula for Calculating Total Surface Area of a Pyramid

The total surface area of a pyramid is the sum of the lateral surface area and the base area of that pyramid.

Stp$S_{tp}$ = Sxq$S_{xq}$ + Sđáy$S_{đáy}$

III. Illustrative Examples

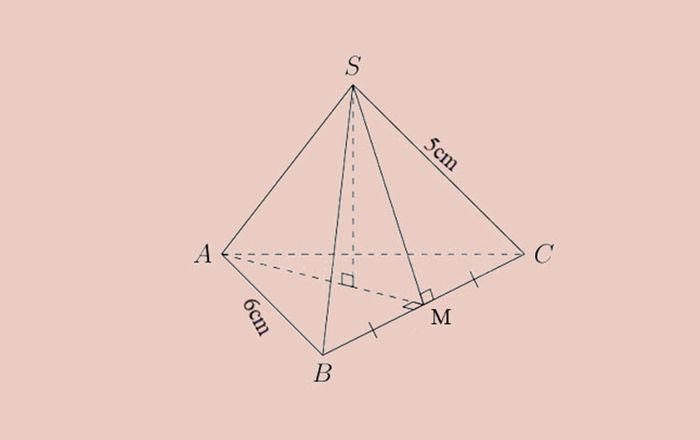
Example 1: Given an equilateral triangular pyramid with a base edge of 6 cm and lateral edges of length 5 cm. Calculate the lateral surface area and the total surface area.

Solution

- Given a problem involving an equilateral triangular pyramid with a base edge of 6 cm, making all sides of the base triangle equal to 6 cm, and the length of the lateral edges of the pyramid is 5 cm.

- Let's call the equilateral triangular pyramid S.ABC, where S is the apex. Draw a line connecting S to the midpoint of segment AC, denoted as M in the diagram. This is precisely the midsegment d of the equilateral triangular pyramid S.ABC.

- Since triangle SBC is an isosceles triangle at S, triangle SBM is a right-angled triangle at M. BM is half of BC and equals 3 cm. Applying the Pythagorean theorem to the right-angled triangle SBM, we have:

SM2=SB2−BM2=52−32=16$S{M}^2=S{B}^2-B{M}^2=5^2-3^2=16$

=> SM = 4 cm (SM is the midsegment d of the pyramid).

- Applying the formula for the lateral surface area of the pyramid, we have:

- Area of the base triangle is: SArea of the base =a2×√34=62×√34=9√3 cm2

- Applying the formula for the total surface area of the pyramid, we get:

STotal surface area =S+S=36+9√3≈51,59 cm2$S_{tp}=S_{xq}+S_d=36+9\sqrt{3}\approx 51,59{cm}^2$

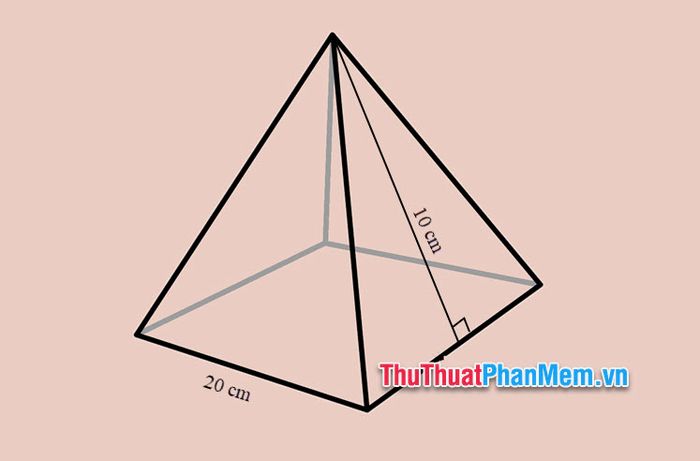
Example 2: For a regular quadrilateral pyramid with the height of each triangular side being 10 cm and the length of the base side being 20 cm. Calculate the total surface area of the regular quadrilateral pyramid.

Solution

As it's a regular quadrilateral pyramid, all sides of the base quadrilateral are 20 cm.

The lateral area (triangular face) of the pyramid is:

S=12×10×20=100 cm2$S=\frac{1}{2}\times 10\times 20=100{cm}^2$

Therefore, the lateral surface area of the pyramid is:

Sxq=4×100=400 cm2$S_{xq}=4\times 100=400{cm}^2$

Applying the formula for the total surface area of the pyramid, we get:

Stp=Sxq+Sa=400+20.20=800 cm2$S_{tp}=S_{xq}+S_a=400+20.20=800{cm}^2$

So, the total surface area of the pyramid is 800 cm2$800{cm}^2$.

Therefore, Mytour has shared with you the formula for calculating the surface area of a pyramid, the formula for calculating the lateral surface area, the formula for calculating the total surface area, and illustrative examples. With these useful knowledge about pyramids, we hope you will have a better understanding to easily solve problems related to pyramid surface area. Thank you for your interest and for following this article.