Formula for Rhombus Diagonal Calculation & Illustrative Examples

Are you looking for the formula to calculate the diagonal of a rhombus? Whether it's a rhombus or any other geometric shape, each has its own set of formulas. Besides calculating the area and perimeter of a rhombus, calculating its diagonal is also a common and important problem in geometry. Join us at Mytour to explore the formula for rhombus diagonal calculation & illustrative examples in the article below.

I. What is a Rhombus? What is a Rhombus Diagonal?

A rhombus in Euclidean geometry is a quadrilateral with all four sides equal. It's a parallelogram with opposite sides equal or a parallelogram with diagonals perpendicular to each other.

Properties of Rhombus

• Opposite angles are equal
• Two diagonals are perpendicular to each other and bisect each other at their midpoints
• Diagonals are angle bisectors of the rhombus
• A rhombus has all properties of a parallelogram (opposite sides are parallel and equal; opposite angles are equal; diagonals bisect each other at their midpoints)

Rhombus Diagonal is the line connecting two opposite vertices of a rhombus, dividing it into two congruent triangles with equal sides. A rhombus has two diagonals, intersecting each other at the midpoint of the rhombus.

II. Formula for Rhombus Diagonal Calculation

1. Formula for Rhombus Diagonal Calculation based on the Formula for Rhombus Area

Using the formula for rhombus area: S=d1×d22$S=\frac{d_1\times d_2}{2}$

Where: S is the area of the rhombus; d1 and d2$d_1\text{ and }{d}_2$ are the two diagonals of the rhombus.

From this, we have the formula for rhombus diagonal calculation as d1=S×2d2$d_1=\frac{S\times 2}{d_2}$ or d2=S×2d1$d_2=\frac{S\times 2}{d_1}$

2. Formula for Rhombus Diagonal Calculation based on Cosine Law

The cosine law expresses the relationship between the lengths of the sides of a triangle and the cosine of the corresponding angle.

Cosine formula: c2=a2+b2+2abcosγ$c^2=a^2+b^2+2ab\cos \gamma$

Where: a, b, c are the sides of the triangle, γ is the angle between sides a and b.

3. Formula for Rhombus Diagonal Calculation based on Pythagorean Theorem

Applying the Pythagorean theorem to the right triangle with the right angle at the intersection of the two diagonals of the rhombus. The square of the hypotenuse will be equal to the sum of the squares of the other two sides.

Example 1: Given rhombus ABCD with side a and angle ABC = 60 degrees. Calculate the two diagonals of the rhombus.

Solution

Because a rhombus has equal sides, rhombus ABCD has all sides equal to a.

Considering triangle ABCD: AB = BC = a

Angle ABC = 60 degrees.

=> Triangle ABC is an equilateral triangle with side length a.

So AB = AC = BC = a. The length of the main diagonal AC = a.

Let I be the intersection of the two diagonals, applying the Pythagorean theorem to the right triangle ABI we have:

BI2=AB2−AI2=a2−(a2)2=a2(1−14)=34a2$B{I}^2=A{B}^2-A{I}^2=a^2-{\left(\frac{a}{2}\right)}^2=a^2\left(1-\frac{1}{4}\right)=\frac{3}{4}{a}^2$

=> BI=a√32$BI=\frac{a\sqrt{3}}{2}$

Thus, diagonal BD = BI x 2 = a√3$a\sqrt{3}$

III. Illustrative Example

Type 1: The problem provides the length of one diagonal and asks students to find the length of the other diagonal.

Example 2: A rhombus has a small diagonal measuring 4 cm, and the long diagonal is twice the length of the small diagonal. Calculate the length of the long diagonal?

Solution

Let the small and large diagonals of the rhombus be d1$d_1$ and d2$d_2$.

We have: d1$d_1$ = 4cm and d2$d_2$ is twice d1$d_1$.

Hence, the length of the large diagonal d2$d_2$ = 4 x 2 = 8 cm.

Example 3: A rhombus has the difference in length of its two diagonals as 10 cm. The first diagonal is 3 times the second diagonal. Find the lengths of the two diagonals?

Solution

Let the large and small diagonals of the rhombus be d1$d_1$ and d2$d_2$

b. d1$d_1$ - d2$d_2$ = 10cm, d1$d_1$ = 3d2$d_2$

Therefore: 3d2$d_2$ - d2$d_2$ = 10 hence d2$d_2$ = 5cm, d1$d_1$ = 15cm.

Type 2: Problems given area and length of 1 diagonal

For this problem, you only need to apply the formula for finding the rhombus diagonal based on the area given above.

Example 4: Given a rhombus with an area of 200 square cm, and the length of 1 diagonal is 10. Find the length of the other diagonal.

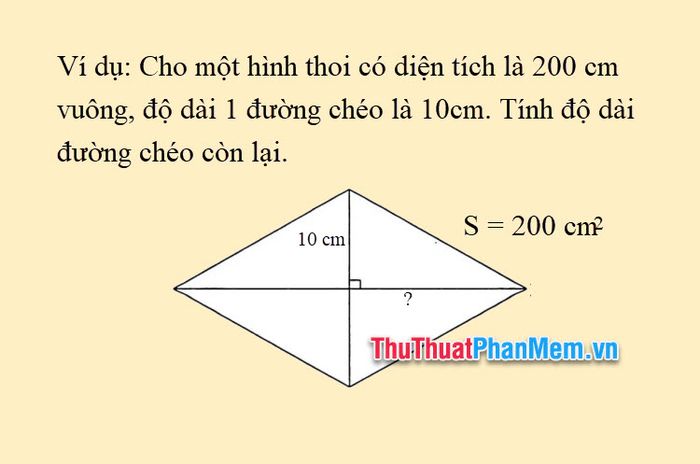
Solution:

Applying the formula for finding the rhombus diagonal based on the rhombus area d1=s×2d2$d1=\frac{s\times 2}{d2}$ we have:

The other diagonal is: (200 x 2) : 10 = 40 cm.

So, the other diagonal of the rhombus is 40 cm long.

Type 3: Problem gives the side and height of the rhombus, asks students to find the lengths of the two diagonals.

Example 5: Given rhombus ABCD with a side of 12.5cm, a height of 6.72 cm, and AC shorter than BD. Find the lengths of the two diagonals AC and BD respectively.

Solution

Applying the formula for calculating the area of the rhombus: S = h x a = 6.72 x 12.5 = 84cm².

=> 2AC x BD = 336

Let O be the intersection point of the two diagonals of the rhombus.

Considering right triangle AOB, we have AC² + BD² = OA² + OB²

where OA = 1/2 AC; OB = 1/2 BD => 12.5², 5² = (AC² + BD²)/4 <=> 625 = AC² + BD²

=> AC + BD = 31 (1).

AC² + BD² = 625 <=> AC² + BD² - AC x AB = 625 - 336 <=> (BD - AC)² = 289

=> BD – AC = 17 (Given BD > AC) (2)

From (1) and (2), we have: BD = 24, AC = 7cm.

Above, Mytour has shared with you the fundamental concepts about rhombus, the formula for calculating the diagonal of a rhombus based on area, the formula for calculating the diagonal of a rhombus according to the cosine law, the formula for calculating the diagonal of a rhombus according to the Pythagorean theorem, and specific illustrative examples. Hopefully, after referring to this article, you will have a clearer understanding of how to calculate the diagonal of a rhombus and be able to easily solve exercises on calculating the diagonal of a rhombus. Thank you for your interest and for following this article.