The sphere is a common geometric shape not only in mathematics but also in many fields and everyday life. Understanding the sphere, the formula for calculating the surface area of a sphere, you can quickly solve problems related to spheres both in studies and daily life. Join Mytour to explore the sphere, the formula for calculating the surface area of a sphere & illustrative examples in the article below.

I. What is a Sphere? What is the Surface Area of a Sphere?
Sphere is a three-dimensional circular object, with each point on its surface equidistant from the center. The sphere is formed by point O as the center, and the length R as the radius of the sphere. When rotating a half-circle around the fixed diameter, the radius R around a fixed diameter results in a sphere.

Radius of a sphere is the distance from the center of a sphere to its surface. The surface area of a sphere is the sum of the areas of all parts of the sphere. By definition, the surface area of a sphere is calculated as 4 times the area of a large circle, or 4 times the constant Pi multiplied by the square of the radius of the sphere.
II. Formula for calculating the surface area of a sphere
Formula for calculating the surface area of a sphere: S = 4πr² = πd²
Where:
- The surface area (S) of a sphere is calculated using the formula: S = 4πr², where r is the radius of the sphere.

For a hemisphere, the surface area (S) is half the surface area of the sphere plus the area of the circular base.
The surface area of a hemisphere (S) = 2πr² + πr² = 3πr².
III. Exercises on calculating the surface area of a sphere.
1. Calculate the surface area of a sphere given its radius.
This type of exercise provides the radius of the sphere and requires finding its surface area.
Solution: Simply apply the formula for the surface area of a sphere S = 4πr², where r is the given radius.

2. Calculate the surface area of a sphere given its diameter.
This exercise type provides the diameter of the sphere and asks for its surface area.
Solution: Simply calculate the radius of the sphere by dividing the diameter by 2, then apply the formula for the surface area of a sphere.
Alternatively, you can use the formula to find the radius of the sphere from the diameter S = πd².
3. Calculate the surface area of a sphere given its volume.
This type of exercise provides the volume of the sphere and asks for its surface area.
Solution: Use the formula for the volume of a sphere to find the radius.
After finding the radius of the sphere, apply the formula for the surface area to calculate the area.
After obtaining the radius of the sphere, apply the formula for the surface area to find the area.

IV. Illustrative Examples
Example 1: Given a sphere with a radius of 6cm from the center O. Find the surface area of the sphere.
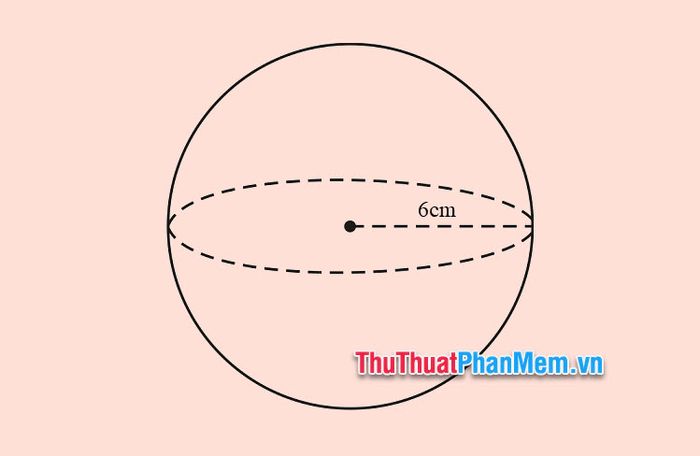
Solution
We have the radius of the sphere r = 6 cm. Apply the formula for the surface area of the sphere S = 4πr².
So, the surface area of the sphere is .
Example 2: Given a sphere with a diameter of 10 cm. Calculate the surface area of the sphere.
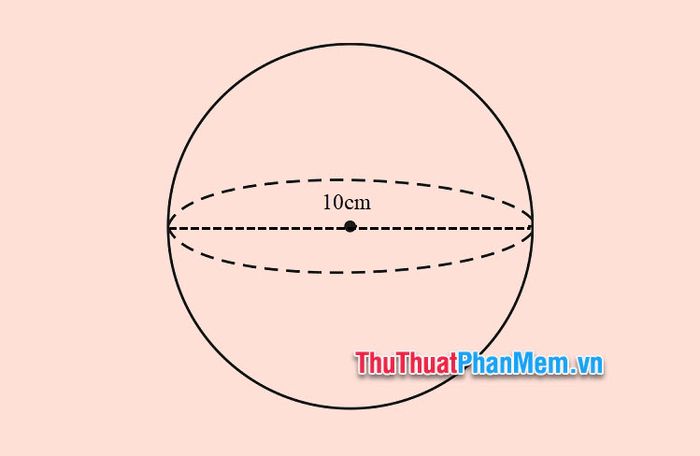
Solution
Using the formula for the surface area of a sphere based on its diameter ,
We have:
So, the surface area of the sphere is .
Example 3: Given a sphere with a volume of V = 900 cm^3. Calculate the surface area of the sphere.
Solution
Using the formula for the radius of a sphere, we have:
The radius of the sphere is approximately 6.345 cm
The formula for the surface area of the sphere is:
The surface area of the sphere is 505,909 cm².
Mytour has shared with you what a sphere is, the formula for calculating the surface area of a sphere, various exercises on calculating the surface area of a sphere, and specific illustrative examples. Hope with this knowledge about spheres, you will grasp the formula for calculating the surface area of a sphere better, combined with the knowledge you have learned, you can quickly solve various exercises on the surface area of spheres. Thank you for your interest and for following this article.
