Formula for the surface area of a cube & examples

If you're not yet familiar with the cube, join Mytour to explore the cube, the formula for the surface area of a cube, and examples in the article below.

I. What is a cube?

A cube is a three-dimensional shape with equal width, length, and height. It has 6 faces, each of which is a square of equal size. In other words, a cube is a rectangular box with all sides being equal.

Properties of a cube

• A cube has 8 symmetrical planes.
• A cube has 12 equal edges, 8 vertices, and every 3 edges meet at one vertex.
• The diagonal of a cube is equal in length.
• A cube has 4 diagonals intersecting at a point, considered as the center of symmetry of the cube.

II. Formula for the surface area of a cube

Given a cube

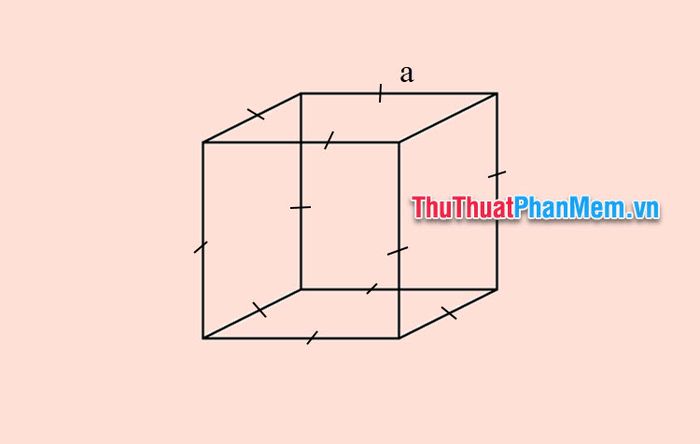
Some conventions:

• a: The length of the cube's edge
• P: The perimeter of the cube
• Sbm$S_{bm}$: Surface area of the cube
• Sxq$S_{xq}$: Surface area around the cube
• Stp$S_{tp}$: Total surface area of the cube
• V: Volume

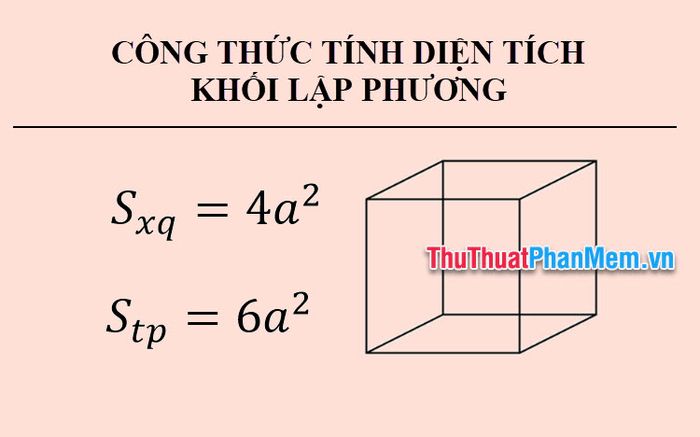
1. Formula for the surface area around the cube

The formula for the surface area around the cube is:

Sxq=4a2$S_{xq}=4a^2$

2. Formula for calculating the total surface area of a cube

The formula for calculating the total surface area of a cube is:

Stp=6a2$S_{tp}=6a^2$

3. Statement in words

- The surface area around the cube is equal to the square of the length of one edge multiplied by 4.

- The total surface area of the cube is equal to the square of the length of one edge multiplied by 6.

- The surface area around only considers the planes outside the cube, while the total surface area includes the area of the planes inside the cube.

III. Exercises on finding the surface area around and total surface area of a cube

Some common exercises on finding the surface area around or the total surface area of a cube.

1. Given the edge of a cube, find the surface area of the cube

In this type of exercise, the problem will provide the edge length of the cube and ask to calculate either the surface area around or the total surface area of the cube.

Solution: Simply apply the formula for finding the surface area around or the total surface area of the cube.

2. Given the surface area of the cube, find the area of one face

The problem will provide either the surface area around or the total surface area of the cube, and it requires finding the area of one face of the cube.

Solution: You just need to remember how to calculate the area of one face based on the given surface area around or total surface area. This type of problem can be easily solved.

• Area of one face of the cube = Surface area around : 4
• Area of one face of the cube = Total surface area : 6

3. Given the area of the cube, find the length of one side.

The exercise provides either the surface area around or the total surface area of the cube and asks for the length of one side of the cube.

Solution: First, calculate the area of one face of the cube based on the given surface area around or total surface area.

To find the side length, use the area of the square as it represents the area of one face of the cube.

IV. Illustrative Examples of Cube Surface Area Calculation

Example 1: Calculate the surface area around and the total surface area of a cube with a side length of 6cm.

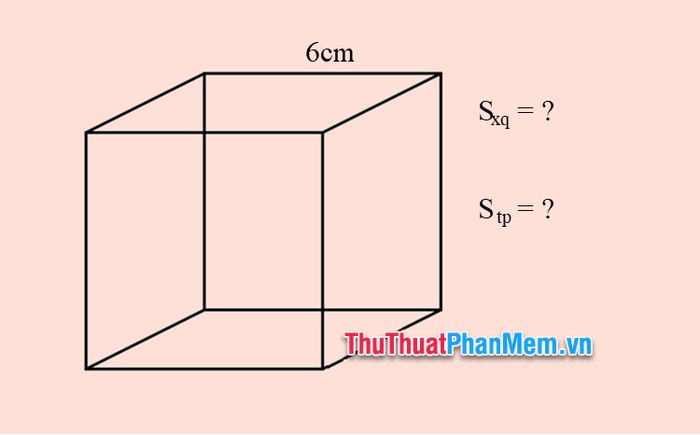
Solution

Applying the formula for surface area, we have:

Sxq=4⋅a2=4⋅62=144$S_{xq}=4\cdot a^2=4\cdot 6^2=144$

Stp=6⋅a2=6⋅62=216$S_{tp}=6\cdot a^2=6\cdot 6^2=216$

So, the surface area of the cube is 144 cm2${cm}^2$.

The total surface area of the cube is 216 cm2${cm}^2$

Example 2: Given a cube with a surface area of 900 cm2${cm}^2$. Calculate the total surface area of the cube.

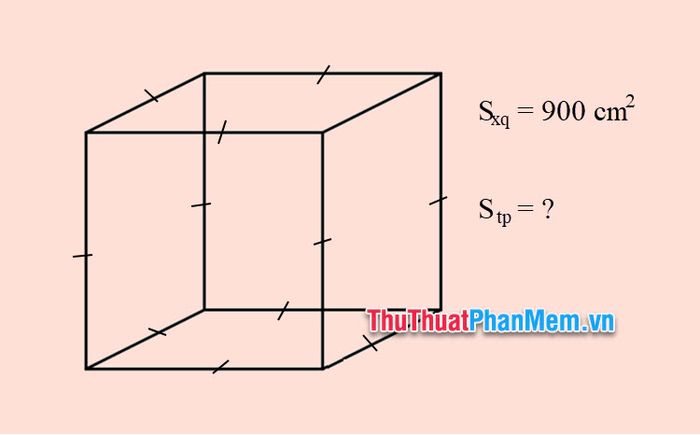
Solution

Applying the formula for surface area Sxq=4a2$S_{xq}=4a^2$, we get:

a=√Sxq4=√9004=√225=15 cm$a=\sqrt{\frac{S_{xq}}{4}}=\sqrt{\frac{900}{4}}=\sqrt{225}=15cm$

Apply the formula for total surface area Stp=6a2$S_{tp}=6a^2$, we get:

Stp=6.a2=6.152=1350 cm2$S_{tp}=6.a^2={6.15}^2=1350{cm}^2$

So, the total surface area of the cube is 1350 cm2$1350{cm}^2$

In this journey with Mytour, you have just explored the world of cubic blocks, unraveling the secrets of the cubic volume formula and practical examples. With the knowledge shared in this article, we hope to enhance your understanding of cubic volumes, aiding you in solving complex problems related to calculating the volume of a cube. Thank you for your interest and following along with this post.