Buzz
In the field of economics, marginal utility (MU) serves as a measure to gauge the value or satisfaction derived by a consumer from the consumption of a product or service. In essence, MU quantifies the change in total utility divided by the change in the quantity of goods consumed. Put simply, MU represents the additional satisfaction gained from each extra unit of consumption.
Procedures
Applying the Marginal Utility Formula
Grasp the economic notion of utility. Utility signifies the 'value' or 'satisfaction' obtained by a consumer through the consumption of goods. A useful way to conceptualize it is that utility reflects how much money a consumer would theoretically be willing to pay for the satisfaction provided by a good.
- For instance, suppose you're hungry and decide to purchase fish for dinner. Let's assume each fish costs $2. If your hunger is such that you'd be willing to pay $8 for the fish, then the fish offers $8 worth of utility. In essence, you're prepared to spend $8 to attain the satisfaction derived from the fish, irrespective of its actual price.
Determine the total satisfaction from consuming a specific quantity of goods. Total satisfaction extends the concept of utility to multiple goods. If consuming one unit of a good yields a certain level of satisfaction, consuming more units of the same good can yield a higher, lower, or equivalent level of satisfaction.
- For instance, suppose you plan to eat two fish. However, after consuming the first fish, your hunger diminishes. Now, you would only pay $6 for the additional satisfaction from the second fish. The second fish is not as valuable to you now that you're partially full. Consequently, the two fish together provide a total satisfaction of $6 + $8 (from the first fish) = $14.
- Note that whether you actually purchase the second fish is irrelevant. Marginal utility (MU) is concerned solely with what you would be willing to pay for it. In practice, economists utilize intricate mathematical models to forecast what consumers would hypothetically pay for goods.
Determine the total satisfaction from consuming a different quantity of goods. To calculate MU, you require two different measurements of total satisfaction. The disparity between them is utilized in the MU computation.
- Continuing the previous example, let's assume you decide to eat four entire fish. Following the consumption of the second fish, you feel somewhat satiated, willing to pay approximately $3 for the subsequent fish. After the third fish, you're nearly full, willing to pay only $1 for the final fish.
- The satisfaction you derive from it is nearly offset by the feeling of fullness. Hence, the four fish collectively provide a total satisfaction of $8 + $6 + $3 + $1 = $18.
Compute MU. Determine the change in total satisfaction over the change in quantity. The resulting value represents the marginal utility, or the satisfaction provided by each additional unit consumed. In the previous example, you would calculate MU as follows:
- $18 - $14 (from the previous step) = $4
- 4 (fish) - 2 (fish) = 2
- $4/2 = $2
- This indicates that, between the second and fourth fish, each additional fish contributes only $2 of satisfaction. This is an average figure; the third fish is actually worth $3, and the fourth is worth $1, naturally.
Calculating MU for Additional Units
Utilize the equation to determine the MU for each extra unit. In the previous scenario, we computed the average MU for multiple goods consumed. While this is a valid approach to MU, it's more commonly applied to individual units of consumed goods. This yields the precise MU for each additional good (not an average).
- Finding this is simpler than it seems. Simply employ the standard equation to ascertain the MU when the change in the quantity of consumed goods is one.
- In the preceding example, you already possess the MUs for each individual unit. When you haven't consumed any fish, the MU of the first fish is $8 ($8 of total satisfaction - the $0 you had previously/change of 1 unit), the MU of the second fish is $6 ($14 of total satisfaction - the $8 you had previously/change of 1 unit), and so forth.
Apply the equation to optimize your utility. In economic theory, consumers strategize on how to allocate their funds to maximize utility. Essentially, consumers aim to attain the greatest satisfaction possible for their expenditure. Consequently, consumers will purchase goods until the marginal utility of acquiring an additional unit is less than the marginal cost (the price of an extra unit).
EXPERT TIP
Paridhi Jain
Certified Public Accountant
Certified Public Accountant
Marginal utility denotes the additional satisfaction gained from further purchases. As purchases increase, the incremental usefulness of additional quantities typically diminishes. For instance, the second pair of shoes may offer less delight compared to the first pair, which is a necessity. This concept elucidates why individuals are willing to pay more for essentials as opposed to discretionary items.
Evaluate forfeited utility. Let's revisit the earlier scenario. Initially, we established that each fish costs $2. Subsequently, we determined the marginal utility (MU) of each fish: $8 for the first, $6 for the second, $3 for the third, and $1 for the fourth.
- With this data, you would opt out of purchasing the fourth fish. Its MU ($1) falls short of its marginal cost ($2). Essentially, you're experiencing a loss of utility in this transaction, making it unfavorable.
Employing a Marginal Utility Table
| Tickets Bought | Total utility | Marginal utility |
|---|---|---|
| 1 | 10 | 10 |
| 2 | 18 | 8 |
| 3 | 24 | 6 |
| 4 | 28 | 4 |
| 5 | 30 | 2 |
| 6 | 30 | 0 |
| 7 | 28 | -2 |
| 8 | 18 | -10 |
Allocate columns for quantity, total utility, and marginal utility. Most MU tables contain these three columns, sometimes more. The critical data is typically arranged from left to right.
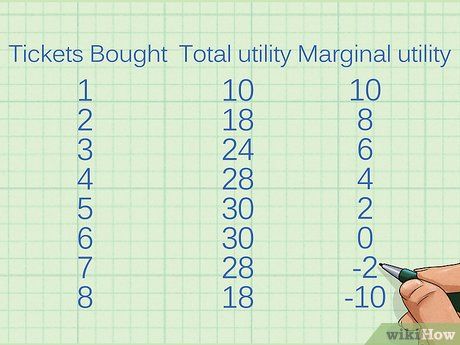
- It's important to note that the column headings may vary. For instance, the 'Quantity' column could be labeled as 'Items purchased' or 'Units acquired.' The key aspect is the information within the column.
Identify a trend of diminishing returns. A standard MU table illustrates that as consumers acquire more of a particular good, their desire for additional units diminishes. Post a certain threshold, the marginal utility of each extra unit starts to decline. Consequently, the overall satisfaction diminishes following additional purchases.
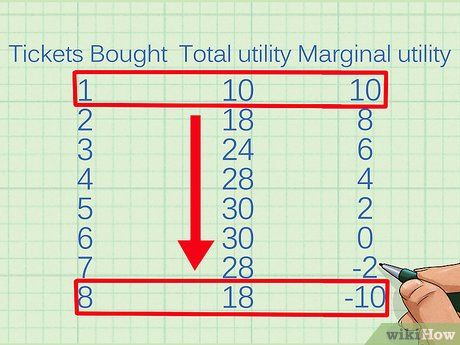
- In the provided chart, the trend of diminishing returns is evident from the outset. Initially, each ticket to the film festival yields significant marginal utility. However, beyond the first ticket, subsequent tickets provide diminishing returns. Following six tickets, each additional ticket results in negative MU, decreasing overall satisfaction. This could be attributed to consumer fatigue from repetitive movie viewings.
Evaluate Optimal Utility. This is the stage where marginal cost surpasses MU. A marginal utility table facilitates the prediction of a consumer's purchase behavior. Typically, consumers continue purchasing goods until the marginal cost (the cost of one additional unit) exceeds the MU. By identifying the cost of goods outlined in the chart, the point of utility maximization is the last row where MU exceeds the marginal cost.
- For instance, if the tickets in the chart cost $3 each, utility is optimized when the consumer acquires 4 tickets. Subsequent tickets yield an MU of $2, which falls short of the $3 marginal cost.
- It's noteworthy that utility isn't necessarily maximized when MU becomes negative. Goods can still provide some benefit to the consumer without being deemed 'worth it.' For example, the fifth ticket in the chart maintains a $2 MU. Although not negative, it contributes to a reduction in total utility as it doesn't justify the cost.
Analyze chart data for additional insights. Once you've established the fundamental columns mentioned above, extracting further numerical information about the scenario becomes straightforward. This is particularly convenient when using spreadsheet software like Microsoft Excel, which can perform calculations effortlessly. Here are two additional types of data you may consider incorporating into columns to the right of the original three:
- Average Utility: Obtained by dividing the total utility in each row by the quantity of goods purchased.
- Consumer Surplus: Calculated by subtracting the product's marginal cost from the marginal utility in each row. It signifies the 'profit' in terms of utility that the consumer gains from purchasing each product. This concept is also known as 'economic surplus.'
Insights
-
It's crucial to recognize that the examples presented represent model scenarios. They depict hypothetical consumers rather than real ones. In reality, consumers may not always act rationally; their purchasing behavior might deviate from the utility-maximizing ideal. While economic models provide valuable insights into broad consumer behavior trends, they may not perfectly align with real-world situations.
-
If you include a consumer surplus column in your chart (as outlined earlier), utility maximization occurs at the last row before the consumer surplus turns negative.
