How to Compute Stock Correlation Coefficient

Buzz

Content

Standard Deviation and Covariance

Correlation Coefficient

Utilization of correlation coefficients

Understanding whether two stocks tend to move in sync is valuable. When constructing a diversified portfolio, it's essential to include stocks with differing trends. The Pearson Correlation Coefficient offers insight into the relationship between the returns of distinct stocks.

Steps

Standard Deviation and Covariance

Collect stock returns. To compute the correlation coefficient, gather data on returns (daily price fluctuations) for two stocks within the same timeframe. Returns are determined by the difference in closing prices of the stocks across two consecutive trading days. For instance, if a stock closes at $2.00 on Tuesday and $2.04 on Wednesday, the return is 2 percent.

Stock price data can be sourced from market-tracking platforms like Bloomberg and Yahoo! Finance.
Organize the returns chronologically, labeling the two stocks as X and Y for simplicity.
For example, stock X's data might be 0.9, 1.3, 1.7, 0.4, 0.7 over five days, while stock Y's data could be 2.5, 3.5, 3.6, 3.1, 2.3.
Correlation coefficients may fluctuate or change signs over time (from positive to negative), emphasizing the significance of the chosen timeframe.
Short-term traders might opt for 20 or 50 days' worth of data, whereas long-term investors may prefer 150 or 250.

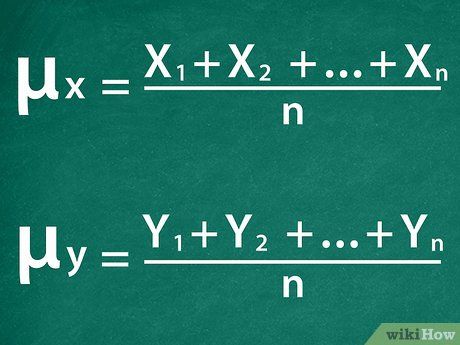Compute the average for each group.

μ

μ_{x}

μ_{y}

μ_{x} = \frac{0.9 + 1.3 + 1.7 + 0.4 + 0.7}{5}

μ_{y} = \frac{2.5 + 3.5 + 3.6 + 3.1 + 2.3}{5}

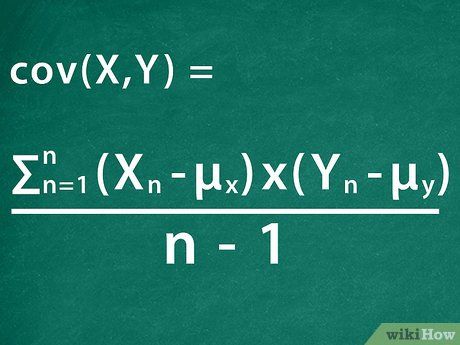Determine the covariance.

σ_{x y} = \sum_{n = 1}^{n} (X_{n} - μ_{x}) \times (Y_{n}

− μ y ) n − 1 {\displaystyle \sigma _{xy}={\frac {\sum _{n=1}^{n}(X_{n}-\mu _{x})\times (Y_{n}-\mu _{y})}{n-1}}}

X_{n}

Y_{n}

(0.9 - 1.0) \times (2.5 - 3.0)

\frac{0.77}{4}

The covariance of returns for stocks X and Y is 0.1925.

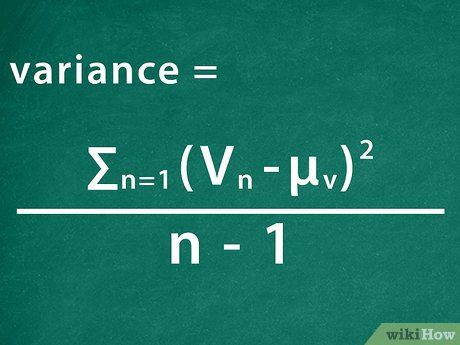Determine the variance for each individual stock.

\frac{\sum_{n = 1}^{n} (V_{n} - μ_{V})^{2}}{n - 1}

(0.9 - 1.0)^{2}

n - 1

σ_{x}^{2}

σ_{y}^{2} = 0.272

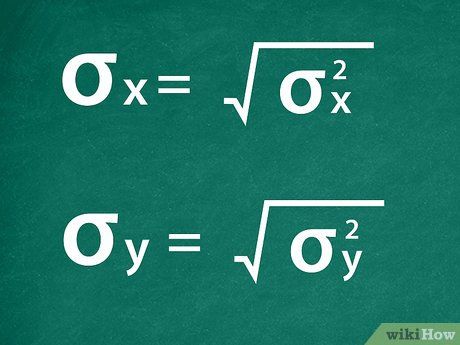Calculate the standard deviation.

σ

Take the square root variance

σ_{x}^{2}

σ_{y}^{2}

σ_{x} = 0.456

σ_{y} = 0.522

The calculations have been rounded to three decimal places for easier later computations. Maintaining more decimal places in your calculations will enhance accuracy.

Correlation Coefficient

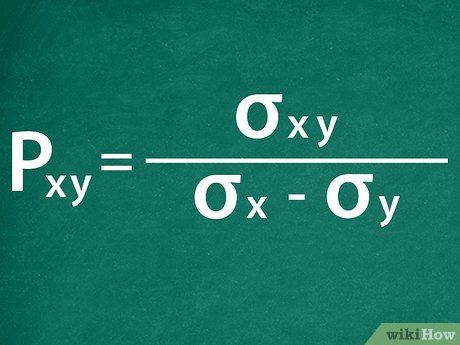Establish your correlation coefficient equation.

ρ_{x y}

\frac{σ_{x y}}{σ x \times σ y}

Find the correlation coefficient.

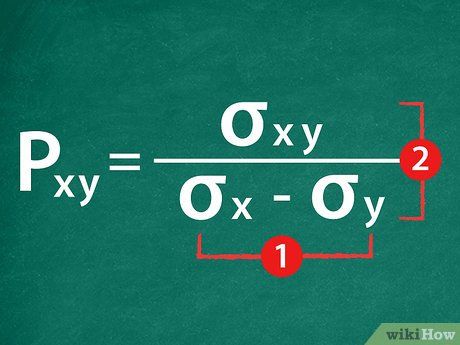Determine the correlation coefficient.

ρ_{x y} = 0.809

This result has been rounded to three decimal places.

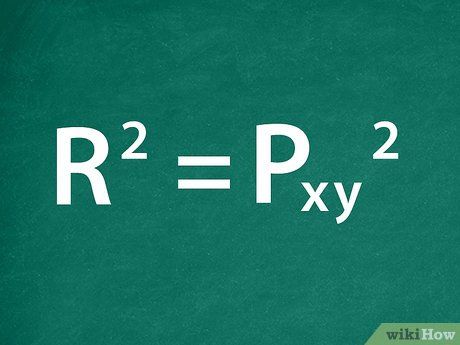Calculate R-squared.Coefficient of determination

r_{x y}^{2} = {0.809}^{2} = 0.654.

Utilization of correlation coefficients

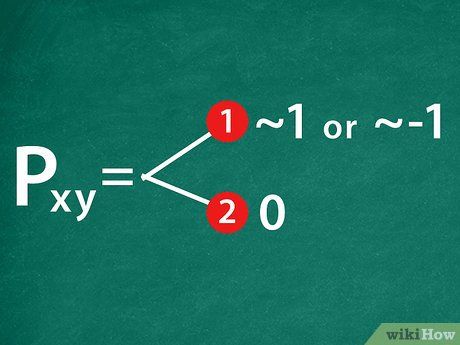
Interpret your correlation coefficient outcome. The correlation coefficient serves as an indicator for two aspects. Firstly, it reflects whether the two variables typically exhibit simultaneous movement in the same direction. A positive coefficient signifies such correlation, while a negative one indicates the opposite. Secondly, it gauges the similarity in these movements. A coefficient nearing 1 or -1 implies perfect positive or negative correlation, respectively.

Correlation coefficients range between 1 and -1. A value of 0 denotes no correlation.
For instance, a coefficient of 0.809, as in the prior example, suggests a high correlation between stocks X and Y. Both securities tend to move in tandem and with comparable magnitude.

Minimize risk within your investment portfolio. Correlation coefficients primarily aid in structuring diversified securities portfolios. Stocks or assets within a portfolio are compared to determine their correlation coefficient. The objective is to include stocks with low or negative correlations in the same portfolio. Consequently, when one stock's price fluctuates, the other is likely to move in the opposite or independent direction, facilitating effective portfolio diversification.

This approach mitigates 'unsystematic risk,' inherent to individual securities.

Extend your analysis to alternative assets. Apart from stocks, the correlation coefficient is commonly utilized to evaluate relationships among various datasets, including mutual fund returns, Exchange Traded Fund (ETF) returns, and market indexes. By calculating correlations between these datasets and stock returns, portfolio diversification can be achieved or the impact of market shifts on a stock's price movement can be predicted.

For instance, if the stock price of a gold mining company exhibits a high, positive correlation with the price of gold, an investor may anticipate that an increase in gold price would also drive up the company's stock price.

Graph stock return pairs to generate a 'scatter plot'. Utilize spreadsheet software to plot your stocks' dates and returns, facilitating data analysis. Additionally, employing spreadsheet tools, you can plot a regression line representing the best fit to the data.

In Excel, adding this line is achieved by selecting 'Chart' and then 'Add Trendline.' The software automatically calculates a trend line based on your data.
The correlation coefficient assesses how closely the two stock returns adhere to the regression line, indicating the degree of conformity to a linear relation such as Y = βX + α, where α and β are constants.

Pointers

The content is developed by the Mytour team with the aim of customer care and solely to inspire travel experiences. We do not take responsibility for or provide advice for other purposes.

If you find this article inappropriate or containing errors, please contact us via email at [email protected]

Frequently Asked Questions

What is the significance of the Pearson Correlation Coefficient in stock analysis?

The Pearson Correlation Coefficient is crucial for understanding the relationship between the returns of two stocks. It helps investors gauge whether stocks move in sync, aiding in the construction of a diversified portfolio.

How do you collect stock returns for calculating the correlation coefficient?

To collect stock returns, gather daily price fluctuations for two stocks over a consistent timeframe. Calculate returns by finding the difference in closing prices between consecutive trading days, and organize this data chronologically.

What steps are involved in calculating the correlation coefficient for stocks?

Calculating the correlation coefficient involves gathering stock returns, computing the averages, determining covariance, calculating variances, finding standard deviations, and finally applying these values in the correlation coefficient formula.

How does a correlation coefficient of 0.809 affect investment decisions?

A correlation coefficient of 0.809 indicates a high positive correlation between two stocks, suggesting they move together. This insight helps investors in portfolio diversification to minimize risk by choosing stocks with low or negative correlations.

Can the correlation coefficient be used for assets other than stocks?

Yes, the correlation coefficient is applicable to various datasets beyond stocks, including mutual funds, ETFs, and market indexes. This versatility aids in understanding relationships across different investment types.

What is the purpose of using a scatter plot in stock return analysis?

A scatter plot visually represents the relationship between stock returns, allowing investors to analyze trends and correlations easily. It also facilitates the addition of a regression line to assess linear relationships more effectively.