How to Determine the Effective Interest Rate

Buzz

Content

Comprehending Effective Interest Rate

Compute the Effective Interest Rate

Guide to Calculating Effective Interest Rates: Glossary, Calculator, Practice Problems, and Solutions

Calculating the effective interest rate becomes a walk in the park with these formulas.

Key Points to Remember

The effective interest rate surpasses the nominal interest rate as it considers compounding interest.

r = (1 + i / n)^{n} - 1

r = e^{i} - 1

Procedures

Comprehending Effective Interest Rate

Get acquainted with the concept of effective interest rate. The effective interest rate delineates the total borrowing cost, incorporating the impact of compounded interest, which is disregarded in the nominal or 'stated' interest rate.

Ascertain the stated interest rate. The stated (or nominal) interest rate is the publicly advertised interest rate. It serves as the 'headline' rate that lenders typically promote on loans, investments, and savings accounts. The stated interest rate is usually expressed as a percentage.

Verify the frequency of compounding periods for the loan. Compounding periods typically occur monthly, quarterly, annually, or continuously. This indicates how often interest is applied.

Commonly, compounding occurs monthly. However, it's advisable to confirm this with your lender.

Compute the Effective Interest Rate

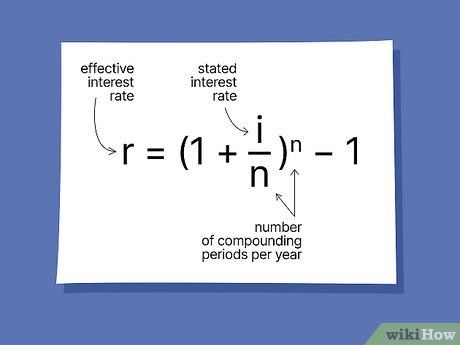Grasp the formula for converting a stated interest rate into an effective interest rate.

r = (1 + i / n)^{n} - 1.

In this equation, r denotes the effective interest rate, i represents the stated interest rate, and n denotes the number of compounding periods per year.

Apply the provided formula to determine the effective interest rate. For instance, let's say you have a loan with a stated interest rate of 5%, compounded monthly. Substituting these values into the formula results in: r = (1 + .05/12)¹² - 1, or r = 5.12%. Similarly, if the loan is compounded daily, the calculation becomes: r = (1 + .05/365)³⁶⁵ - 1, yielding r = 5.13%. It's important to note that the effective interest rate always exceeds the stated rate.

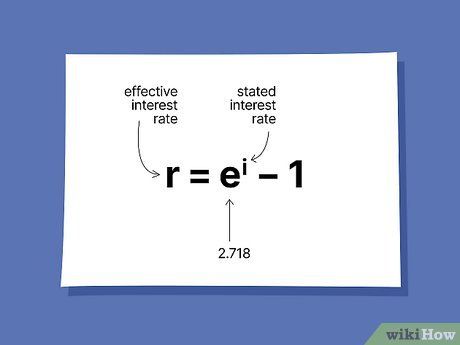Utilize an alternate formula if interest undergoes continuous compounding.

r = e^{i} - 1

Determine the effective interest rate for continuously compounded interest. For example, suppose you have a loan with a nominal interest rate of 9%, compounded continuously. Applying the formula yields: r = 2.718^.09 - 1, resulting in an effective rate of 9.417%.

Employ a simplified approach to compute the effective interest rate. Once you grasp the principles behind effective interest rates, there's a straightforward method to calculate it:

Utilize the formula ((Number of intervals × 100 + interest) ÷ (Number of intervals × 100))^{Number of intervals} × 100
Determine the number of intervals per year. For instance, semi-annual compounding occurs 2 times annually, quarterly 4 times, monthly 12 times, and daily 365 times.
Multiply the number of intervals per year by 100 and add the interest rate.
- For a 5% interest rate, semi-annually it becomes (2 × 100 + 5%) or 205. For quarterly, it's 405, 1,205 for monthly, and 36,505 for daily compounding.
Apply the above formula to find the effective interest rate:
- Semi-annually: ((Number of intervals × 100 + interest) ÷ (Number of intervals × 100))² × 100 = ((205)÷(200))² × 100 = 105.0625
- Quarterly: ((405)÷(400))⁴ ×100 = 105.095
- Monthly: ((1,205)÷(1,200))¹² ×100=105.116
- Daily: ((36,505)÷(36,500))³⁶⁵ ×100 = 105.127
The effective interest is the excess over 100 when the principal is 100.
- For the semi-annual calculation, the excess over 100 is 5.0625%. Therefore, this is the effective interest rate for semi-annual compounding. For quarterly compounding, it is 5.095%, 5.116% for monthly, and 5.127% for daily.

Guide to Calculating Effective Interest Rates: Glossary, Calculator, Practice Problems, and Solutions

Example Glossary for Calculating Effective Interest Rates

Example Effective Interest Rate Calculator

Sample Practice Problems for Calculating Effective Interest Rates

Solutions for Sample Calculating Effective Interest Rate Problems

Quick Tips

Utilize various online calculators to swiftly determine the effective interest rate. Moreover, Microsoft Excel's EFFECT() function can compute the effective rate based on the nominal rate and compounding periods.

The content is developed by the Mytour team with the aim of customer care and solely to inspire travel experiences. We do not take responsibility for or provide advice for other purposes.

If you find this article inappropriate or containing errors, please contact us via email at [email protected]

Frequently Asked Questions

What is the difference between effective interest rate and nominal interest rate?

The effective interest rate accounts for compounding, making it higher than the nominal rate. It reflects the true cost of borrowing by including interest accrued over time.

How can I calculate the effective interest rate from a stated interest rate?

To calculate the effective interest rate, use the formula r = (1 + i/n)ⁿ - 1, where 'i' is the nominal interest rate and 'n' is the number of compounding periods per year.

Is there a formula for calculating the effective interest rate with continuous compounding?

Yes, for continuous compounding, use the formula r = e^i - 1, where 'e' is the base of the natural logarithm and 'i' is the nominal interest rate.

Can online calculators assist in determining the effective interest rate?

Yes, various online calculators can quickly compute the effective interest rate. Tools like Microsoft Excel also have built-in functions for this purpose, making calculations easier.