This article unveils the powerful SKEW function, a staple in Excel's statistical arsenal.

Description: The SKEW function measures distribution asymmetry, revealing how skewed a distribution is around its axis.
- Negative Skewness: Indicates a distribution with an extended tail towards negative values.
Positive skewness: The distribution is skewed asymmetrically with more extension towards positive values.
Syntax: SKEW(number1, [number2], ...)
Where:
- number1, [number2], ...): Values for which skewness is to be calculated. number1 is mandatory, followed by optional values containing a maximum of 255 number parameters.
Attention:
- The values of the parameters must be numbers, names, arrays, or references containing numbers.
- Logical values and textual number representations when directly entered into the parameter list -> still get computed.
- Parameters that are text or error values unable to be converted to numerical type -> causing the function to fail.
If the argument is an array reference containing text or logic values -> these values are ignored, however, the value 0 is still counted.
If there are fewer than 3 data points or the standard deviation is 0 -> the function returns an error value #DIV/0.
The deviation equation is defined by the formula:
n(n−1)(n−2)∑(xi−¯xs)3
For example:
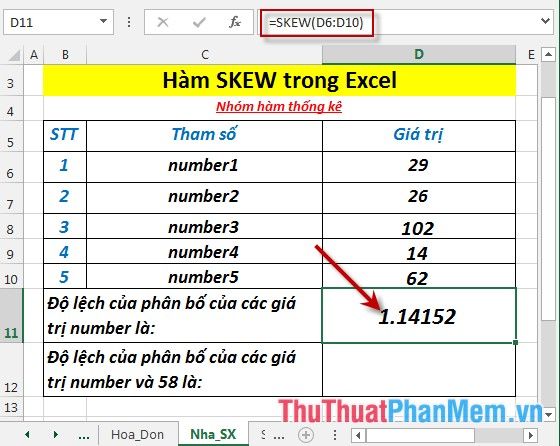
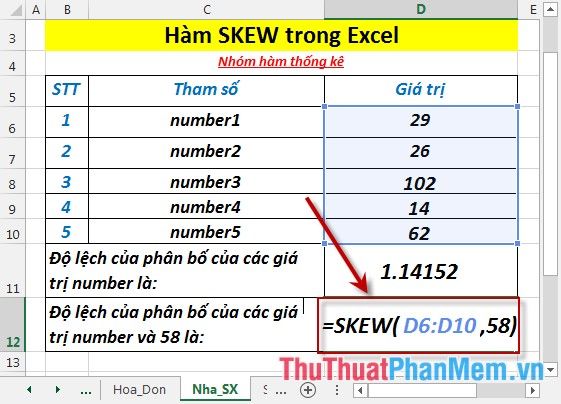
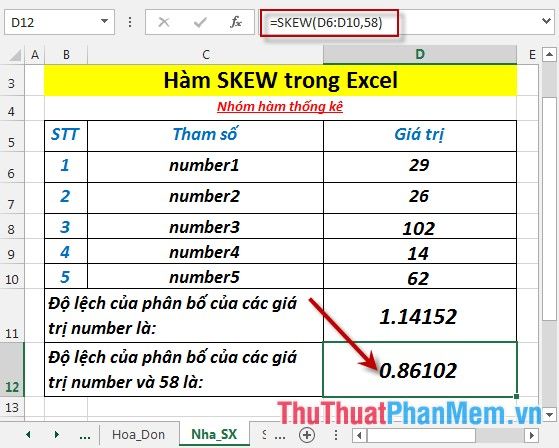
Calculate the skewness of the distribution of values in the following dataset:
To find the skewness of the distribution of numbers, enter the formula in the cell where you want the result: =SKEW(D6:D10)
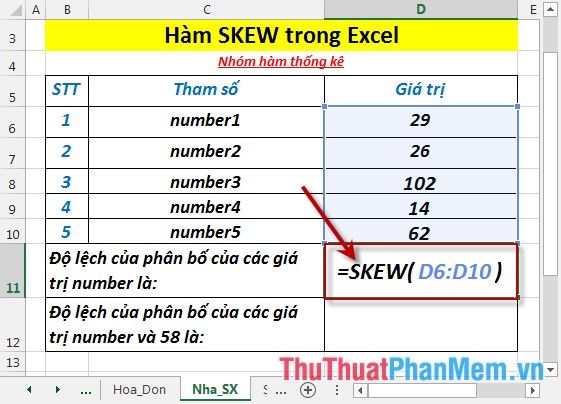
Press Enter. The skewness of the distribution of numbers is: