Mastering Rectangle Length Calculation: A Quick Guide

Rectangle length calculation is a fundamental geometry task often encountered by students. This brief guide aims to simplify the concept for students and parents, focusing on essential formulas and applications without delving into complex explanations.

Rectangle Basics

What Defines a Rectangle?

In mathematics, a rectangle is identified as a quadrilateral featuring four right angles (90°), with pairs of opposite sides being equal in length. The longer sides define the rectangle's length, while the shorter sides determine its width.

Identifying a Rectangle

Key Indicators of a Rectangle:

• A quadrilateral where three angles measure 90°.
• An isosceles trapezoid with one 90° angle.
• A parallelogram with equal diagonal lengths or one angle measuring 90°.

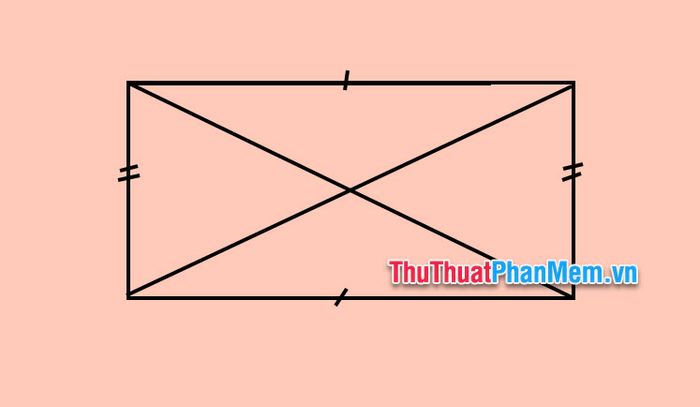
Properties of a Rectangle

A rectangle combines the properties of an isosceles trapezoid and a parallelogram, including:

• Equal diagonal lengths, with their intersection being the midpoint of each.
• Opposite sides are parallel and equal in length.
• The intersection of diagonals divides the rectangle into four congruent isosceles triangles.

Rectangle Calculation Formulas

The perimeter of a rectangle is the total length of its sides. To calculate, add the length and width and then multiply by 2.

Rectangle Perimeter Formula

Rectangle perimeter is the outline around the shape, calculated as the sum of all sides. Mathematically, 'To find a rectangle's perimeter, add its length and width and multiply by 2', ensuring the same units are used.

Perimeter formula: P = (length + width) * 2

Definitions:

• P: Represents the perimeter of the rectangle.
• a: The length of the rectangle.
• b: The width of the rectangle.

Rectangle Perimeter Calculation Example

For rectangle ABCD with a length of 10 cm and a width of 6 cm, the perimeter is calculated.

Solution:

Using the formula for the perimeter of a rectangle, we get:

PABCD = (length + width) * 2 = (10 + 6) * 2 = 32 cm.

Therefore, the perimeter of rectangle ABCD is 32 cm.

2. Rectangle Area Formula

The area of a rectangle, measured in square units, represents its surface size. To calculate it, simply multiply the length by the width, ensuring both are in the same measurement unit.

Area formula for a rectangle: A = length x width

Explanation:

Symbols: S = area, a = length, b = width

This formula is used when the length and width are known. For rectangles where the diagonal's size is known, the area can be calculated differently:

S = 1/2 x (Diagonal)^2

Example on Calculating Rectangle Area

Rectangle ABCD has lengths of 15 cm and width of 10 cm. Calculate its area.

Solution:

Using the area formula for rectangles, we find:

Area of ABCD = length x width = 15 x 10 = 150 cm^2

Thus, the area of rectangle ABCD is 150 cm^2.

3. Formula for calculating the diagonal of a rectangle

The length of a rectangle's diagonal equals the square root of the sum of the squares of its length and width (according to the Pythagorean theorem).

Formula for the diagonal of a rectangle: Diagonal = sqrt(a^2 + b^2)

Definitions:

• a and b represent the lengths of the rectangle's sides.
• The square root symbol indicates the square root operation.

Example: Calculating the Diagonal of a Rectangle

Given rectangle ABCD with lengths AB = CD = 4 cm and widths BC = DA = 3 cm, find the diagonal length.

Solution Overview:

Applying the diagonal formula for a rectangle.

Diagonal AD = BD = √(AB² + BC²) = √(4² + 3²) = √25 = 5 cm.

Thus, the length of the diagonal of rectangle ABCD is 5 cm.

III. Calculating Rectangle Length with Detailed Example

1. Determining Rectangle Length Given Area and Width

To find the length of a rectangle when its area and width are known, use the formula: length = Area / Width = S / b.

Explanation Key:

• 'S' represents the area of the rectangle
• 'a' stands for the rectangle's length
• 'b' indicates the rectangle's width

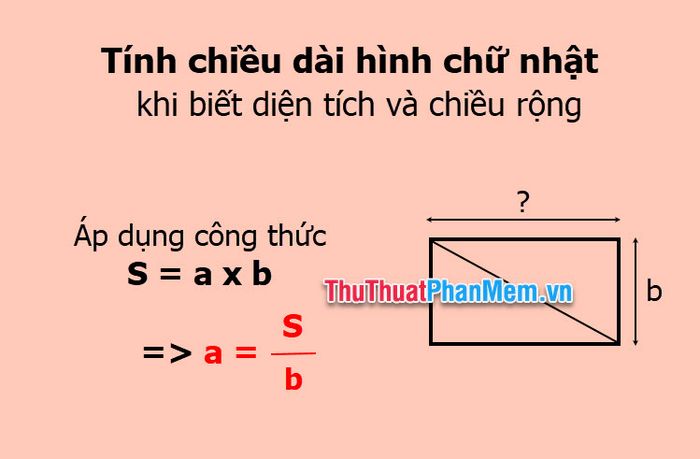
Example: A rectangular backyard has an area of 160m2 and a width of 10m. Determine the length of the backyard.

Solution:

Length 'a' = Area 'S' / Width 'b' = 160 / 10 = 16m.

The backyard length is 16m.

Calculating the rectangle's length with known perimeter and width

To find the rectangle's length with the perimeter and width known, use the formula: Length = (Perimeter / 2) - Width.

Definitions:

Perimeter (P) is the rectangle's perimeter. Half perimeter: P/2. Length (a) is the rectangle's length. Width (b) is the rectangle's width.

Example: Classroom board's perimeter is 8m, width 1m. Calculate the board's length.

Solution:

Using the formula: Length = (Perimeter / 2) - Width = (8 / 2) - 1 = 3m.

The classroom board length is 3m.

Calculating rectangle length without direct width and perimeter values.

To find the rectangle's length when the perimeter and width aren't directly provided, extract width from given data, then calculate length.

Example: A rectangle's perimeter is 72cm, with its width being 1/4 of its half perimeter. What is its length?

Solution starts here.

Half perimeter of the rectangle: 36 cm.

Width of the rectangle: 9 cm.

Therefore, the length of the rectangle is: 27 cm.

This concludes our guide on rectangle-related knowledge, including formulas and calculation methods for rectangle dimensions, with detailed examples. We hope this information helps students gain a clearer understanding of rectangles and boosts their confidence in solving related problems, including calculations of length, width, area, and perimeter.