When sorting and analyzing data, you often need to rank objects based on certain criteria. This article provides a detailed guide on how to use the PERCENTRANK function to determine the rank of a value.
Description: This function returns the rank of a value in a dataset based on a specified criterion. For instance, you can utilize the PERCENTRANK function to assess the exam results of candidates in various tests.
Syntax: PERCENTRANK(array,x,[significance]).
In which:
- array: Represents the data array or range containing the data to be evaluated, which is a required parameter.
- x: The value you want to determine the rank of, which is a required parameter.
- significance: An optional parameter used to determine the number of decimal places returned for the percentage value. If omitted, the default value is 3 decimal places (0,xxx).
Note:
- If the array value is empty, the function returns the #NUM! error.
- If significance < 1, the function returns the #NUM! error.
- In case the value of x does not match any of the comparison values in the array, the PERCENTRANK function performs an interpolation process to return the appropriate value.
Example 1:
Find the rank of the value 25 using the PERCENTRANK function with the following data table:
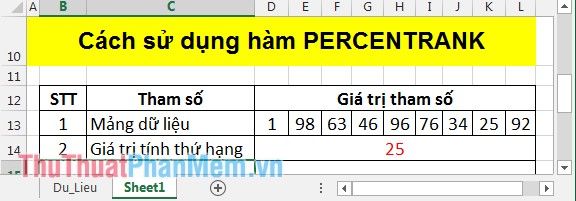
In the cell where you want to calculate, enter the formula: =PERCENTRANK(D13:L13,D14).
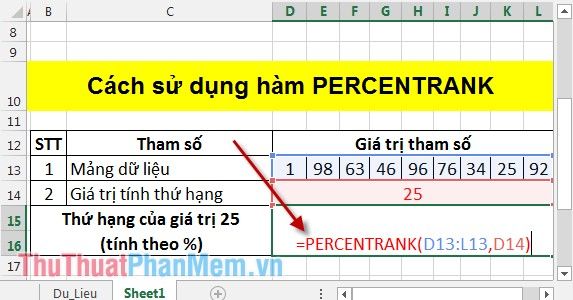
Press Enter and the result is:
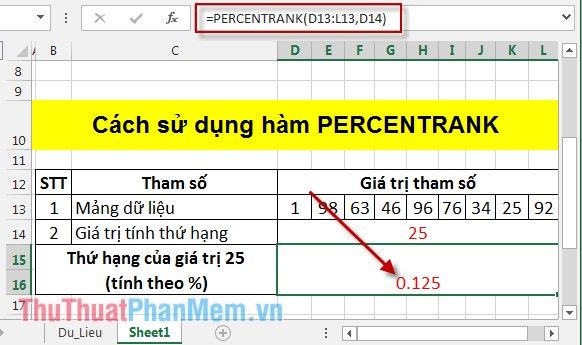
Here, the value 25 in the data array has 1 value smaller than 25 and 7 values larger than 25 => the percentile rank of 25 is 1/ (1+7)= 0.125.
Example 2:
The value for calculating the percentile rank is not present in the data array.
For example, find the percentile rank of the value 15 in the data array:
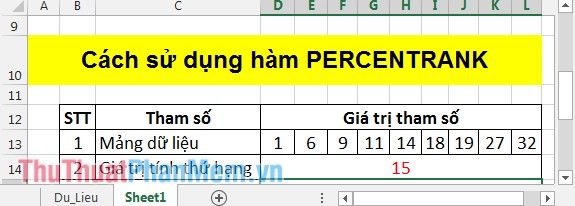
In the cell where you want to calculate, enter the formula =PERCENTRANK(D13:L13,D14) and press Enter, the result is:
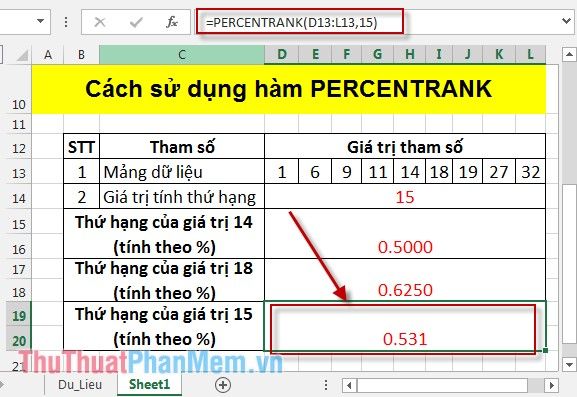
In this example, calculate the PERCENTRANK of the 2 neighboring values of 15, which are 14 and 18.
Since the value 15 is not in the data array, it is calculated based on its two nearest neighbors using the PERCENTRANK values of 14 and 18:
- PERCENTRANK (14) = 0.5
- PERCENTRANK (18) = 0.625
=> PERCENTRANK (15) = 0.5 + (0.25 *(0.625-0.0.5)) = 0.531
So if the value needed to find the percentile rank is not in the data array, the function takes the nearest neighbor value and the number of parts equals the distance between the two neighbors.
The above article introduces in detail how to use and special cases of the PERCENTRANK function.
Wishing you all success!
