Rotational Cylinder Volume Formula & Examples

Understanding the volume of rotational cylinders is crucial in academic curricula and exams. Additionally, it's a common problem across various practical fields. Explore the rotational cylinder volume formula and examples here for better comprehension.

1. What is a Rotational Cylinder?

When rotating a plane figure around a fixed axis, it forms a rotational cylinder. A cylinder is generated by the rotation of a rectangle around a fixed axis.

Rotational cylindrical solid is a form of cylinder and its interior space. The volume of a rotational cylindrical solid is the space occupied by the cylinder within the space.

Some key characteristics of rotational cylindrical solids:

• The base of the solid is a circle, and this circle serves as the lateral surface of the solid when it is rotated around an axis
• The axis of the solid is a line passing through the center of the base and is the rotational axis of the circle when forming the rotational cylindrical solid
• The lateral surface of the solid consists of circles parallel to the base with the same center as the base. These lateral surfaces form the curved surface of the rotational cylindrical solid
• The height of the rotational cylindrical solid is the distance from the base to the top surface of the solid

2. Formula for the volume of a rotational cylindrical solid

To calculate the volume of a rotational cylindrical solid, you need to rely on the area of the circular base and the height of the solid. Specifically, to find the volume of a rotational cylindrical solid, you simply multiply the area of the base by the height of the solid.

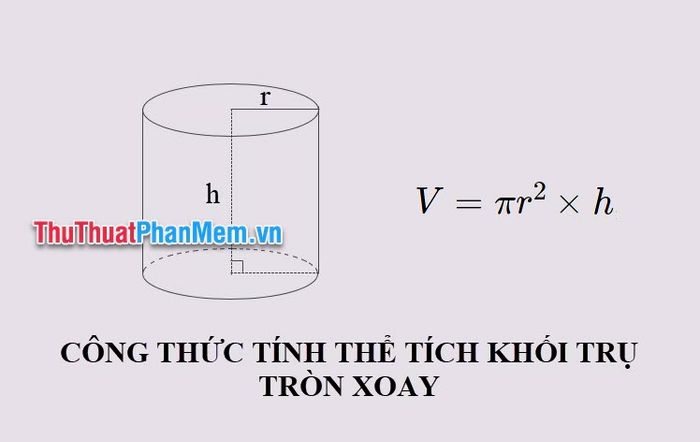
The formula for the volume of a rotational cylindrical solid is: V=Sa×h=πr2×h$V=S_a\times h=\pi r^2\times h$

Where:

• V is the volume of the rotational cylindrical solid
• π is the mathematical constant Pi, approximately equal to 3.14159
• r is the radius of the circular base of the solid (or simply the radius of the base circle)
• h is the height of the rotational cylindrical solid

3. Illustrative Example

Example 1: Given a rotational cylindrical solid with radius r = 5 cm and height h = 12 cm. Calculate the volume of this rotational cylindrical solid?

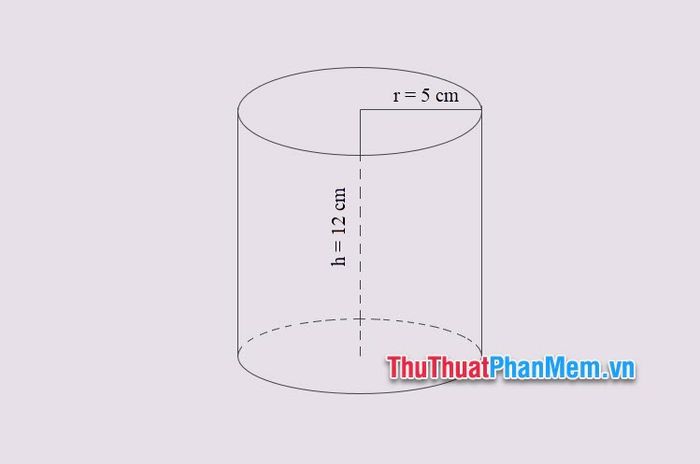
Solution

Applying the formula for the volume of a rotational cylindrical solid V=πr2×h$V=\pi r^2\times h$, we have:

V=π×52×12≈942,478 cm3$V=\pi \times 5^2\times 12\approx 942,478{cm}^3$

The volume of the rotational cylindrical solid is approximately 942,478 cm3$942,478{cm}^3$

Example 2: Given a rotational cylindrical solid with the base being the circumcircle of an equilateral triangle with side length a. Knowing the height of the solid is 3a. Calculate the volume of this rotational cylindrical solid?

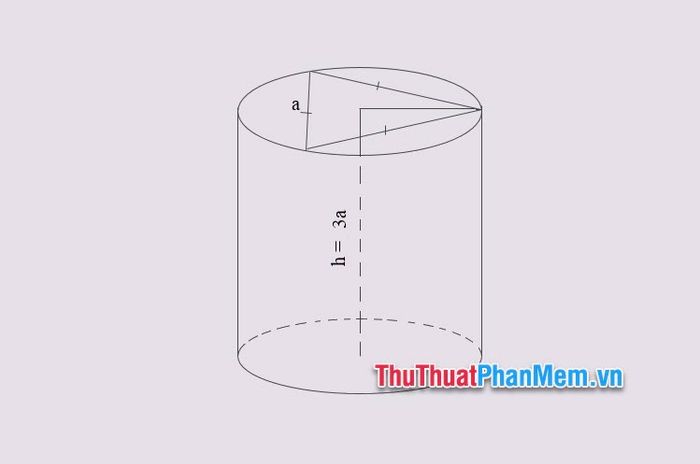
Solution

The base circle is the circumcircle of an equilateral triangle with side length a, so according to the sine theorem, the radius of that circle is

R=a2sin60∘=a2√32=a√3=a√33=a√33$R=\frac{a}{2\sin {60}^{\circ }}=\frac{a}{2\frac{\sqrt{3}}{2}}=\frac{a}{\sqrt{3}}=\frac{a\sqrt{3}}{3}$

Applying the formula for calculating the volume of a rotational cylindrical solid, we have:

V=πr2×h=π(a√33)2×3a=π×3a29×3a=πa3$V=\pi r^2\times h=\pi {\left(\frac{a\sqrt{3}}{3}\right)}^2\times 3a=\pi \times \frac{3a^2}{9}\times 3a=\pi a^3$

So the volume of the rotational cylindrical solid is πa3$\pi a^3$

Above, you have explored with Mytour about the rotational cylindrical solid, the formula for its volume, and specific examples. Hope you've gained useful knowledge, understanding more about the formula for the volume of a rotational cylindrical solid for application when encountering problems or requirements involving the calculation of the volume of a rotational cylindrical solid. Thank you for your interest and following this article.