Understanding the Formulas for Calculating the Radius of a Circle with Illustrative Examples

In geometry, a circle is one of the fundamental shapes that you need to grasp formulas for calculating aspects of circles to solve mathematical exercises related to them. Calculating the radius of a circle is a common type of problem, and it's essential to memorize the formulas. Join us at TechTipsSoftware.com to explore the formulas for calculating the radius of a circle with illustrative examples in the article below.

I. What is the Radius of a Circle?

A circle is a two-dimensional geometric shape formed by the set of all points at a fixed distance (radius) from a fixed point (center) in the plane. It has no edges and no angles.

The diameter of a circle is a straight line passing through the center and having two endpoints touching the circle. The radius is the distance from the center to any point on the circle. The diameter is twice the radius.

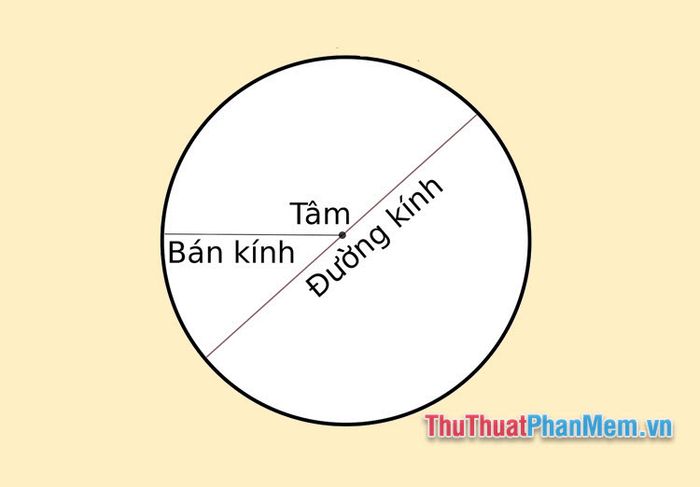
Other important concepts about circles to keep in mind.

• The circumference of a circle, or the length of its boundary, is calculated by multiplying the diameter by 3.14 or the radius by 2 and then multiplying by 3.14.
• The area of a circle is the region inside the circle and is directly proportional to the square of its radius. To calculate the area, people apply the formula involving the constant PI (π = 3.14) and the square of the circle's radius.

II. Formulas for Calculating the Radius of a Circle

To calculate the radius of a circle, you can use three formulas: Calculating the radius based on the diameter (d); calculating the radius based on the area (S); calculating the radius based on the circumference (C).

1. Formula for calculating the radius based on the diameter

Since the radius of a circle (r) is the distance from the center to the circumference, the radius is half the length of the diameter. Therefore, to calculate the radius, you only need to take the diameter and divide it by 2.

The formula for calculating the radius based on the diameter is: r=d2$r=\frac{d}{2}$

Where:

• r : Represents the radius of the circle
• d : Represents the diameter of the circle

2. Formula for calculating the radius based on the area

If the problem provides the area of the circle, you just need to apply the formula for the area of the circle S=πr2$S=\pi r^2$, which leads to the radius of the circle being the square root of the area divided by Pi.

r=√Sπ$r=\sqrt{\frac{S}{\pi }}$

Where:

• Pi is a constant, approximately equal to 3.14.
• r represents the radius of the circle
• S represents the area of the circle

3. Formula for calculating the radius based on the circumference

If the problem provides the circumference of the circle and asks to calculate the radius, you just need to apply the formula for the circumference of the circle C=d×π=2r×π$C=d\times \pi =2r\times \pi$

From this, the formula for calculating the radius of the circle is

Where:

• C: Represents the circumference of the circle
• d: Represents the diameter of the circle
• r: Represents the radius of the circle
• Approximately, Pi is equal to 3.14

III. Illustrative Examples

Example 1: Calculate the radius of a circle given that its diameter is 8cm.

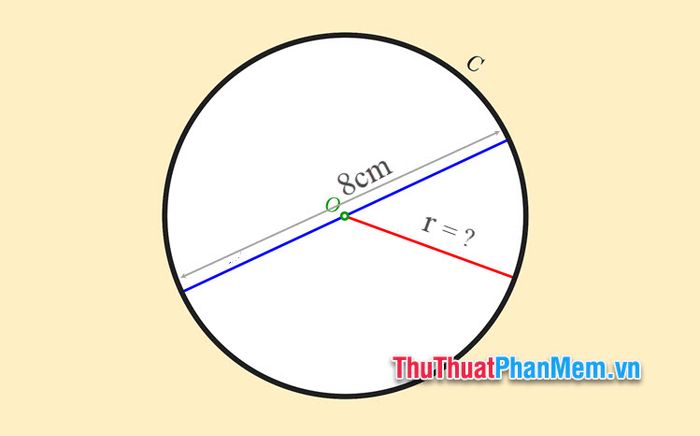
Solution:

Applying the formula r=d2$r=\frac{d}{2}$, we get:

r=d2$r=\frac{d}{2}=\frac{8}{2}=4cm$

So the radius of the circle is 4cm.

Example 2: Calculate the radius of the circle, given that the area of the circle is 28.26 square cm.

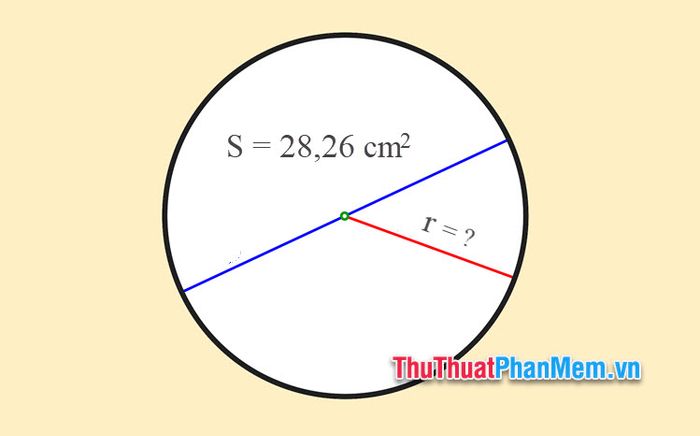
Solution:

Applying the formula to calculate the radius of the circle based on the area r=√Sπ$r=\sqrt{\frac{S}{\pi }}$, we have:

r=√28,263,14=√9=3 cm$r=\sqrt{\frac{S}{\pi }}=\sqrt{\frac{28,26}{3,14}}=\sqrt{9}=3cm$

So, the radius of the circle is 3cm.

Example 3: Calculate the radius of the circle when the circumference of the circle is 25.12 cm.

Solution:

Applying the formula to calculate the circumference of the circle: C=d×π=2r×π$C=d\times \pi =2r\times \pi$

We have: r=cπ×2=25,12π×2=4 cm$r=\frac{c}{\pi \times 2}=\frac{25,12}{\pi \times 2}=4cm$

So, the radius of the circle is 4cm.

You've now explored with Mytour about the radius of a circle, the formula for calculating the circle's radius, and how to compute it with specific examples. With the knowledge shared in this article, it is hoped that you have a clearer understanding of the formula for calculating the circle's radius and can easily solve problems related to it. Thank you for your interest and for following this article.