Have you ever puzzled over how to calculate the volume of a rectangular prism? Or perhaps you find yourself needing to find the volume of one in real-life scenarios. Dive into this article for a clear explanation and method on calculating rectangular prism volume.

In this article, we break down the formula for calculating the volume of a rectangular prism. Join us as we explore and understand.
Understanding the Concept of Rectangular Prism
Exploring the realm of rectangular prisms in geometry, where six congruent faces form its structure. The opposite faces are considered its bases, while the remaining faces constitute its sides. A rectangular prism boasts 12 edges, 8 vertices, and 6 faces.
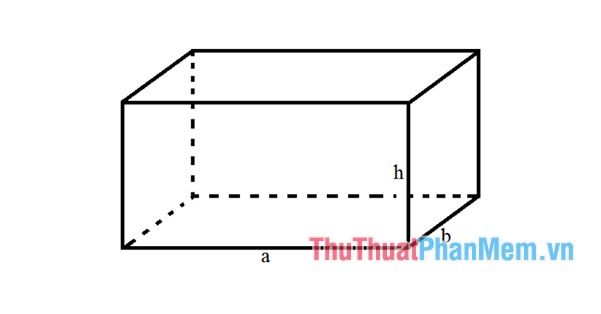
The Formula for Calculating Rectangular Prism Volume
The volume of a rectangular prism equals the product of its base area and height:
V = abh
Volume unit is the cube of distance (distance cubed), with the standard unit for volume measurement being cubic meters (m3)
Where:
- V represents the volume of the rectangular prism.
- a denotes the length of the rectangular base, while b stands for its width.
- a.b signifies the base area of the rectangular prism.
- h is the height of the rectangular prism (also the side length of the prism).
Example of Calculating Rectangular Prism Volume
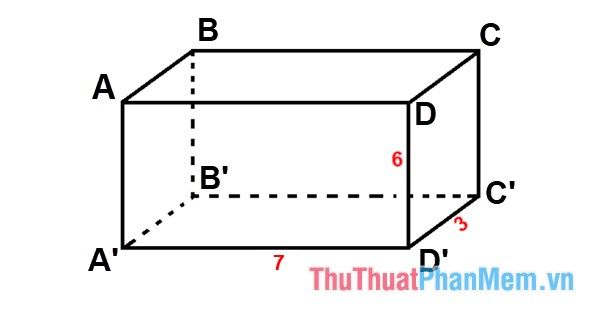
Calculate the volume of rectangular prism ABCD.A’B’C’D’ knowing the base length is 7 cm, base width is 3 cm, and height is 6 cm.
Solution:
Based on the volume formula V = abh
We have: V = 7.3.6 = 126 cm³
Thus, the volume of rectangular prism ABCD.A’B’C’D’ is 126 cm³.
So, this article has shared with you the formula and method for calculating the volume of a rectangular prism. Hopefully, you will understand the formula for calculating the volume of a rectangular prism to apply to specific problems. Wish you success!
