Buzz
Perfect squares are one of the important concepts and forms of mathematics that middle school students need to grasp. So what are perfect squares, what are their properties, is 0 a perfect square? Let's find out all the answers through the article below!
What are perfect squares?
Perfect squares are positive integers that can be expressed as the square of another integer. In other words, a perfect square is the result of multiplying an integer by itself.
Examples:
- 1 is a perfect square (because 1 equals the square of 1).
- 4 is a perfect square (because 4 equals the square of 2).
- 9 is a perfect square (because 9 equals the square of 3).
- 16 is a perfect square (because 16 equals the square of 4).
And so, according to the definition of perfect squares, numbers like 36 (square of 6), 49 (square of 7), 64 (square of 8), 81 (square of 9), ... are also perfect squares.
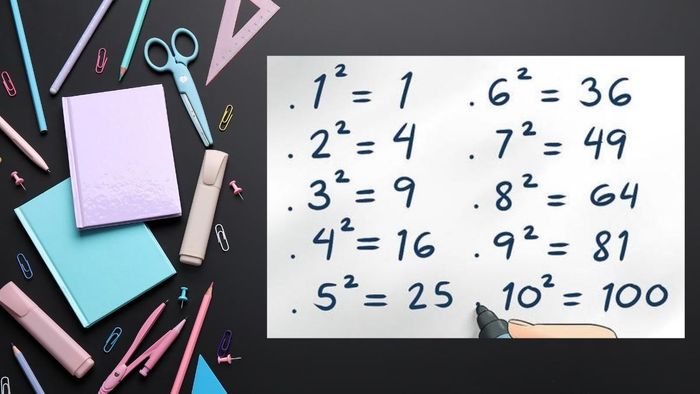Understanding perfect squaresIf the school day is approaching and you are looking for a quality backpack to store your study materials, check out some of the backpack/laptop bags that are currently popular at Mytour:
Properties of Perfect Squares
After knowing what perfect squares are, you also need to understand the properties of this type of number. Some important properties of perfect squares are as follows:
Formula: A perfect square is the square of an integer. That means it has the form n2, where n is an integer.
Sum of consecutive odd numbers: Each perfect square is the sum of consecutive odd numbers starting from 1. Example: 1=1; 4=1+3; 9=1+3+5; 16=1+3+5+7;…
Last digit: In the decimal system, the last digit of a perfect square can only be 0, 1, 4, 5, 6, or 9. There are no perfect squares ending with 2, 3, 7, or 8.
What are the properties of perfect squares?Divisibility property: If a perfect square is divisible by a prime number, then it is also divisible by the square of that prime number. For example, 3 is a prime number and 36 is a perfect square divisible by 3. Thus, 36 is also divisible by 9.
Smallest perfect square
Besides the question of what perfect squares are and their properties, many people also wonder if 0 is a perfect square. The answer is Yes. Because 0 can be represented as the square of 0, which equals 0. And 0 is also the smallest perfect square. However, if considering only the set of positive integers, then the smallest perfect square is 1.
In the set of positive integers less than 100, we have 9 perfect squares. Including: 1 (square of 1), 4 (square of 2), 9 (square of 3), 16 (square of 4), 25 (square of 5), 36 (square of 6), 49 (square of 7), 64 (square of 8), 81 (square of 9).
Largest perfect square
Within each prime number range (1 digit, 2 digits, 3 digits,…), you can find out what the perfect square is and what the largest perfect square is. For example:
- One digit (1-9): The largest perfect square is 9 (square of 3).
- Two digits (10-99): The largest perfect square is 81 (square of 9).
- Three digits (100-999): The largest perfect square is 961 (square of 31).
- Four digits (1000-9999): The largest perfect square is 9801 (square of 99).
- Five digits (10000-99999): The largest perfect square is 99856 (square of 316).
Guide to identifying perfect squares
To identify perfect squares, you can rely on understanding what perfect squares are and their properties. Here are some methods:
Check the square root: Based on the definition, you can determine whether an integer, for example 0, 1, 4, 9, ..., is a perfect square by calculating its square root. For example, 36 is a perfect square. Because the square root of 36 is 6, and 6 is an integer.
Look at the last digit: In the decimal system, the last digit of a perfect square can only be 0, 1, 4, 5, 6, or 9. If the last digit of a number is not one of these, then it's definitely not a perfect square.
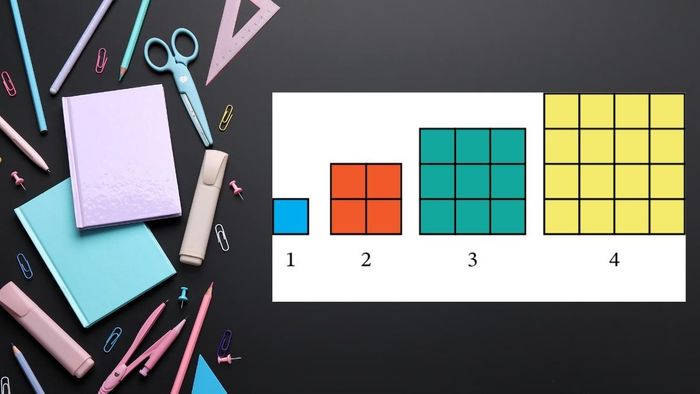Identifying perfect squaresPrime factorization: First, factorize the number into prime factors. If every prime factor appears with an even exponent, then it's a perfect square. Example: 144 = 2²x3² is a perfect square. Because each prime factor (2 and 3) has an even exponent.
Using a perfect square table: If you often need to check what perfect squares are, you can use a basic perfect square table. For example, a table from 1² to 12² for quick reference.
Utilizing computation tools: For large numbers, it's advisable to use a calculator or a computation application to quickly determine whether a number is a perfect square or not.
Synthesis of some types of exercises about perfect squares
So, you've grasped the concept of what perfect squares are, their properties, and how to identify numbers like 0, 1, 4, 9, ... as perfect squares. Let's practice with some characteristic exercises about perfect squares below. This will help you understand more about this type of number in mathematics.
Type 1: Proving perfect squares
You already know whether 0 is a perfect square, but what about in more complex cases? Example: Prove that number B = 4n^4 + 4n³ + n² is a perfect square for all positive integers n.
Solution:
B = 4n^4 + 4n³ + n²= n²(4n² + 4n + 1)= n²(2n + 1)²
We observe that B can be represented as the product of two squares. Or B = [n(2n+1)]², and n(2n + 1) is an integer. Therefore, we conclude that B is a perfect square.
Type 2: Finding n such that a number is a perfect square
To understand what a perfect square is and how to find n for a number to be a perfect square, let's refer to the following exercise.
Example: Find a natural number n such that the following number is a perfect square: B = n² + 4n + 1.
Solution:
Since the number B is a perfect square, we set n² + 4n + 1 = b²
=> 4n²+16n+4=4b²
=> (4n²+16n+16)-16+4=4b²
=> (2n+4)²- 4b² = 12
=> (2n+4+2b)x(2n+4-2b)=12
Observing that 2n+4+2b > 2n+4-2b, and these are all positive integers. Hence, we can find corresponding pairs of numbers: (12, 1), (6, 2), and (4, 3). You need to consider each case to find n and b. Specifically:
- Case 1: (2n + 4 + 2b) (2n + 4 - 2b) = 12 = 12 x 1 => n = 5/4, b = 11/4
- Case 2: (2n + 4 + 2b) (2n + 4 - 2b) = 12 = 6 x 2 => n = 0, b = 1
- Case 3: (2n + 4 + 2b) (2n + 4 - 2b) = 12 = 4 x 3 => n = -1/4, b = 1/4
But n is a natural number, so only the answer n = 0, b = 1 satisfies. And n = 0, implying the perfect square B=1.
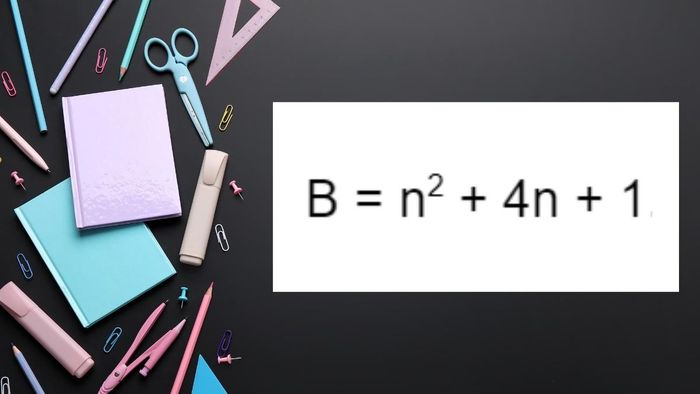Problem type finding n to know what a perfect square isTemporary Conclusion
Thus, the information above will help you understand what perfect squares are as well as some types of perfect square exercises. Hopefully, you grasp what a perfect square is, whether 0 is a perfect square, and many other useful knowledge.
- Explore more in the category: Technology Terms, Industry Terms
