What is the Hyperbolic Function? Formula and Usage

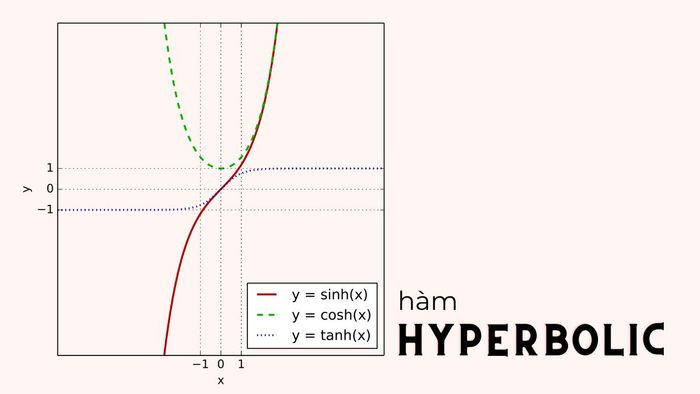
What is the Hyperbolic Function?

The Hyperbolic function performs functions similar to trigonometric functions. If trigonometric functions are represented on a unit circle, Hyperbolic functions are expressed through Hyperbolas.

Additionally, from the logarithmic perspective, the Hyperbolic function is the fractional part of ex, with conditions that the numerator and denominator have degrees not exceeding 2.

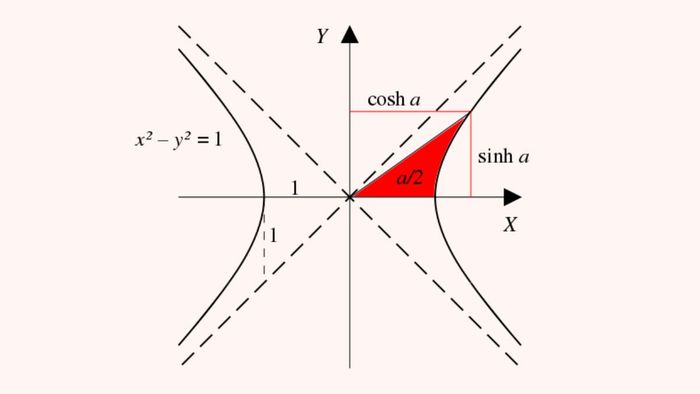
Hyperbolic Function Formula

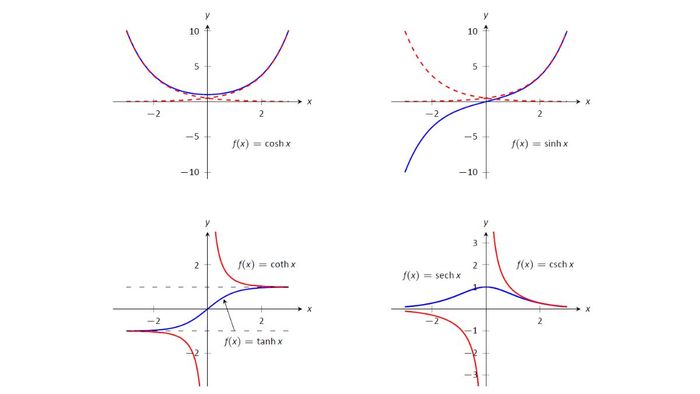
Hyperbolic functions encompass fundamental formulas such as hyperbolic sine - denoted as sinh; hyperbolic cosine - denoted as cosh; and hyperbolic tangent - denoted as tanh. Expanding from these basic formulas, there are extended functions like hyperbolic cotangent - denoted as coth, hyperbolic secant - denoted as sech, and hyperbolic cosecant - csch. Here are the specific formulas for reference:

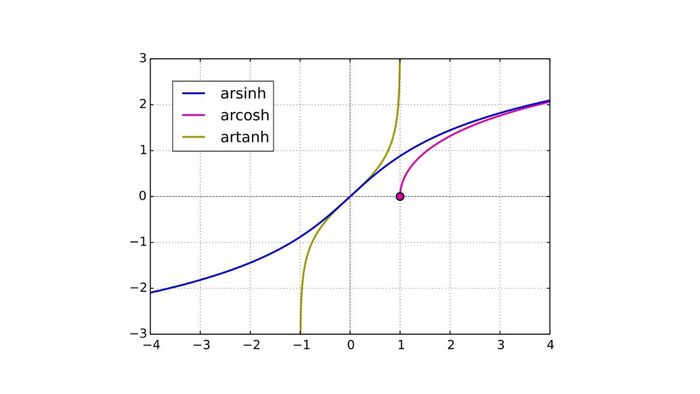
Key Formulas of Inverse Hyperbolic Functions:

• Hyperbolic sine formula: Sinh x = ex - e^(-x)/2 - an odd function, graph symmetric across the x-axis
• Hyperbolic cosine formula: Cosh x = (ex + e^(-x))/2 - an even function, graph symmetric across the y-axis
• Hyperbolic tangent formula: Tanh x = sinh x / cosh x - an odd function, graph symmetric across the x-axis
• Hyperbolic cotangent formula: Coth x = 1 / tanh x - an odd function, graph symmetric across the x-axis
• Hyperbolic secant formula: Sech x = 1 / cosh x - an even function, graph symmetric across the y-axis
• Hyperbolic cosecant formula: Csch x = 1 / sinh x - an odd function, graph symmetric across the x-axis.

Operations like adding arguments, subtracting arguments, and calculating half of an argument can still be performed among hyperbolic functions.

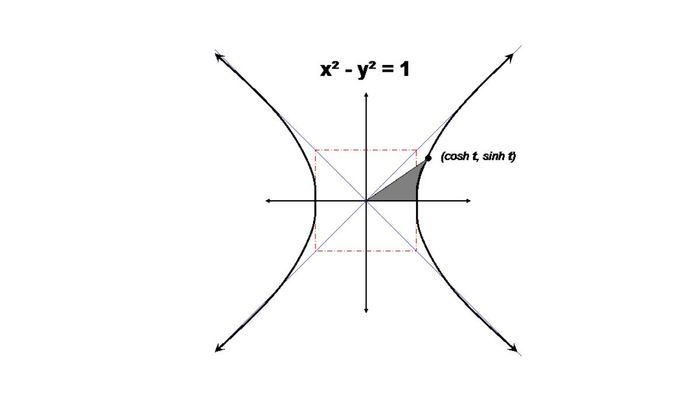
Inverse Hyperbolic Function 

The Inverse Hyperbolic Function, also known as Hyperbolic inverse, is derived by reversing the Hyperbolic function. In many cases, the Inverse Hyperbolic Function is referred to as the 'area function' to recognize the hyperbolic angle.

For each point A (x1, y1) on the Hyperbolic graph, you always obtain the corresponding angle AOx, and the magnitude of this angle represents the Inverse Hyperbolic.

Key Formulas of Inverse Hyperbolic Functions:

• Inverse hyperbolic sine formula: Arsinh x = ln(x + sqrt(x^2 + 1))
• Inverse hyperbolic cosine formula: Arcosh x = ln(x + sqrt(x^2 - 1))
• Inverse hyperbolic tangent formula: Artanh x = 0.5 ln((1 + x) / (1 - x))
• Inverse hyperbolic cotangent formula: Arcoth x = 0.5 ln((x + 1) / (x - 1))
• Inverse hyperbolic secant formula: Arcech x = ln(1 / x + sqrt(1 / x^2 - 1))
• Inverse hyperbolic cosecant formula: Arcsch x = ln(1 / x + sqrt(1 / x^2 + 1))

For some formulas with x in the denominator, you must establish the domain conditions before performing calculations.

Hyperbolic Function for Complex Numbers 

Applying the intimate relationship of Hyperbolic functions to the exponential function is expressed through the identity below:

The equations ex=cosh x + sinh x and e-x=cosh x - sinh x unveil a way to extend the representation of Hyperbolic functions in a complex form.

From there, you can broaden the depiction of Hyperbolic functions under a complex number framework as follows:

Example of Hyperbolic Function

Hyperbolic functions have various applications and different calculation methods. To gain a deeper understanding of these real-world applications, feel free to explore some examples of equations and find the general terms of series using Hyperbolic functions.

Frequently Asked Questions about Hyperbolic Functions

Hyperbolic functions are advanced functions with many applications. So, when applying them, you often have some questions. Let's explore some frequently asked questions right here.

Derivatives of Hyperbolic Functions

The derivatives of Hyperbolic functions are precisely the derivatives of their standard formulas:

• (sinh x)’ = cosh x
• (cosh x)’ = sinh x
• (tanh x)’ = 1 - tanh^2x = sech^2x = acosh^2x
• (coth x)’ = -coth x.csch x
• (sech x)’= -tanh x.sech x

By applying the fundamental derivative formulas of Hyperbolic functions, you can unfold more complex expressions.

Expanding Hyperbolic Functions with Taylor Series 

The Taylor series of a function is the sum of infinitely many terms obtained by taking derivatives of a function at a point. The sum is expressed as:

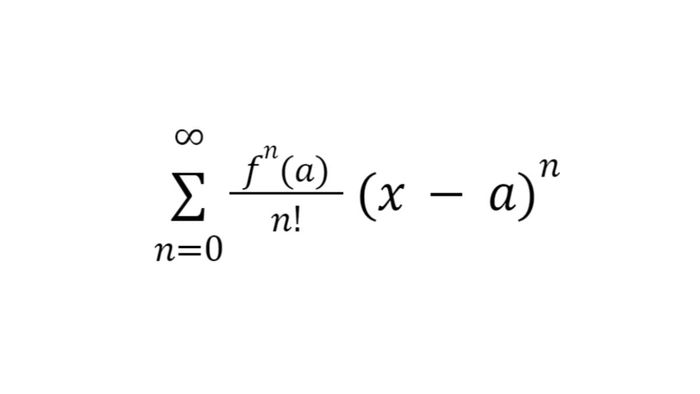
In this context, n represents the degree of the derivative, and a is the point at which you take the derivative.

Building on that theory, various ways to express Hyperbolic formulas using Taylor series are demonstrated as follows:

• sinh x = x + x^3/3! + x^5/5! + x^7/7! +.....=n=0x^(2n+1)/(2n+1)!
• cosh x = x + x^2/2! + x^4/4! + x^6/6! +.....=n=0x^(2n)/(2n)!
• Tanh x = x - x^3/3 + 2x^5/15 - 17x^7/315 +.....=n=0(2n)!(2n-1)B(2n)x^(2n-1)/(2n+1)!, conditions |x| < 2
• Coth x = x^(-1) + x^(-3) - x^(-5) + 2x^(-9) +.....=n=0(2n)!(B(2n)x^(2n-1))/(2n)!, conditions 0<|x|<
• Sech x = 1 - x^2/3 + 5x^4/24 - 61x^6/720 +.....=n=0E(2n)x^(2n)/(2n)!, conditions |x| < 2
• Csch x = x^(-1) - x^(-6) + 7x^(-36) - 31x^(-120) +.....=n=02(1-2^(2n-1))B(2n)x^(2n-1)/(2n)!, conditions 0<|x|<

Where B and E signify the symbols for Bernoulli and Euler numbers, respectively.

Here is the synthesis from Mytour on the theories of Hyperbolic functions. From this, you can apply their properties not only in mathematics but also in various other fields.