Accurate knowledge about the angle between a line and a plane is extremely important for students today. To master this topic, you need to thoroughly understand the theory, grasp problem-solving methods, and apply them flexibly to multiple-choice exercises involving the angle between a line and a plane. The following article will guide you step-by-step, helping you confidently tackle any problem related to this subject.
Definition of the Angle Between a Line and a Plane
To successfully solve spatial geometry problems, the first and most crucial step is to firmly grasp the concept of the angle between a line and a plane. This angle represents the relationship between a line and a plane, helping us visualize and explain how they interact in three-dimensional space. Understanding how to determine and apply this angle will enable us to solve problems effectively.
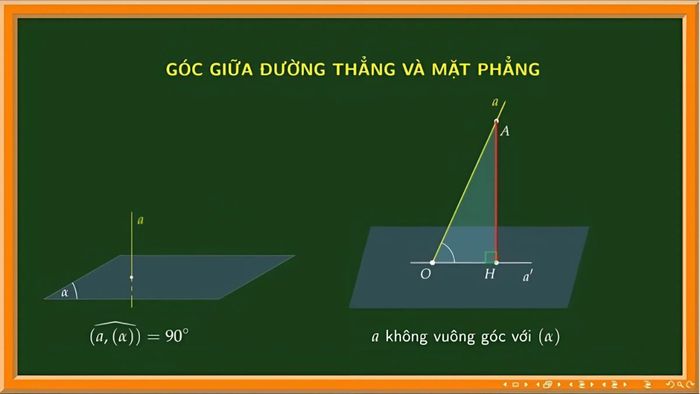
The angle between a line and a plane is the acute angle formed by the line and its intersecting line within the plane. To better understand this definition, you can examine the following two scenarios:
Case 1:
- If plane (P) is perpendicular to line d, then the angle between d and (P) is 900
- In this case, d and (P) do not have a perpendicular projection because d is already completely perpendicular to the plane.
Case 2:
- In the case where line d is not perpendicular to plane (P), the angle formed by d and (P) equals the angle formed by d and its projection on (P), denoted as d'.
- The projection of d on (P), or in other words, the perpendicular projection d', lies entirely within (P) and forms the smallest possible angle with d.
Detailed Notation for the Angle Between a Line and a Plane:
- If d⊥(P) : ∠(d,(P)) = 900
- If d is not perpendicular to (P) : ∠(d,(P)) = ∠(d,d′), which is the angle between d and the perpendicular projection d' of d onto (P).
Step-by-Step Guide to Determining the Angle Between a Line and a Plane
To measure the angle between a plane and a line, a solid understanding of this concept is essential. It acts like a compass guiding you through the maze of spatial geometry. To solve this problem, we need to clearly understand the steps and methods applicable to each specific scenario. This will equip you with the precise methodology to tackle multiple-choice exercises or advanced problems effectively.
Calculating the Angle Between a Line and a Plane Using the Vector Method
To accurately calculate the angle between a plane and a line, you need to be familiar with and understand the geometric tool of vectors. This method is built on the relationship between the direction vector of the line and the normal vector of the plane. First, it’s essential to grasp how to determine the angle between these two elements in the most precise and intuitive way.
To calculate this, you need to identify the normal vector of the plane, denoted as n, and the direction vector of the line, denoted as u. These two tools play a crucial role in defining the relationship between the line and the plane. The formula for calculating the angle is based on the dot product of the two vectors, combined with the magnitude (norm) of each vector to ensure accurate results.
For example, let d be a line with direction vector u = (a, b, c), and P be a plane with normal vector (A, B, C). From this, the angle between the line and the plane can be calculated using the following straightforward formula that anyone can apply:
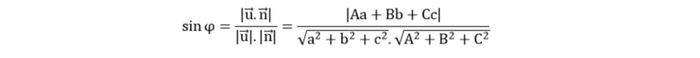
When solving spatial geometry problems, accurately handling calculations and theory is crucial, and this requires reliable tools. For effective learning, a laptop with a strong configuration will help you quickly tackle complex problems. If you're searching for the right device, explore the discounted laptop models at Mytour to find an excellent choice for studying and problem-solving, along with exclusive educational offers.
Determining the Angle Between a Line and a Plane Using Geometric Methods
Calculating the angle between a line and a plane typically relies on the relationship between the projection of the line onto the plane and the line itself. Specifically, the angle between these two elements is understood as the acute angle formed by the line and its projection on the plane.
To solve the problem of finding the angle between line a and plane (α) using geometry, follow these steps sequentially. First, determine the normal vector of plane (α) and the direction vector of line a. Then, apply the angle calculation formula based on the relationship between these two vectors to find the exact value of the desired angle.
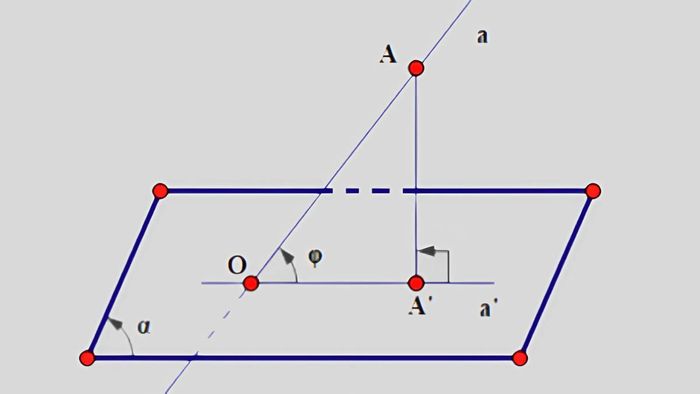
Step 1: Find the Common Point O
To determine the angle between a and (α), the first step is to identify point O, where line a intersects plane (α). This is the point where the line and plane meet, serving as the reference for defining the relationship between these two entities.
Step 2: Perform the Orthogonal Projection of a Point onto the Plane.
Take point A on line a and project it orthogonally onto plane (α). This projected point is denoted as A′. To construct the projection, draw a perpendicular line from A to (α), ensuring that A′ lies within the plane.
Step 3: Quickly Calculate the Angle
From the intersection point O of line a and plane (α), construct a perpendicular segment AA′ from point A on line a to plane (α). The angle ∠AOA′ is precisely the angle between a and (α). To determine the measure of this angle, use a protractor or apply geometric theorems.
Multiple-Choice Exercises Illustrating the Angle Between a Line and a Plane
Below are multiple-choice exercises designed to help you better understand how to determine the angle in specific scenarios.

Question 1: Given ΔABC, right-angled at A, with side AB = a and side AC = a√3. From point A, draw a perpendicular to plane (ABC). On this line, take point S such that segment SA has a length of 2a. Find the angle formed by side SA and the base plane (ABC)?
A. 300
B. 450
C. 600
D. 900
Solution:
Due to the perpendicularity of SA to (ABC), we have
SA⊥(ABC) ⟹ ∠(SA,(ABC)) = 900
Thus, the angle between SA and (ABC) is 900. Therefore, D is the correct answer.
Question 2: Given a pyramid P.MNOP with base MNO being an equilateral triangle of side b. G is the intersection point of the perpendicular dropped from P to plane (MNO). Here, G is not only the projection of P but also the midpoint of segment NO. Additionally, PNO is also an equilateral triangle. Calculate the angle between (MNO) and PM?
A. 300
B. 450
C. 600
D. 900
Solution:
Due to the perpendicularity of PG to (MNO), we have:
PG⊥(MNO)
Thus, MG is the projection of PM onto plane (MNO), so:
∠(PM,(MNO)) = ∠(PM,MG) = ∠(PMG)
Consider triangle PMG
- Since PG⊥(MNO), it follows that PG⊥MGP
- Given that triangle PNO is equilateral, we deduce that PG = MGP
- Triangle PMG is right-angled and isosceles at G, so ∠(PMG) = 450
Therefore, B is the correct answer.
The ability to apply knowledge about the angle between a line and a plane is essential for students to quickly solve problems without excessive deliberation. Mastering the methodology and applying it correctly to multiple-choice exercises will help you achieve high results in exams. This article aims to enhance your understanding and confidence when tackling problems related to this topic.
