Buzz
When evaluating a loan or investment, it may be difficult to visualize the actual cost of the loan or the real return on the investment. There are various terms used to describe the interest rate or profit from a loan, including annual percentage rate, effective interest rate, nominal interest rate, and so on. Among these, the effective interest rate is probably the most useful as it gives you a relatively complete view of the true cost of the loan. To calculate the effective interest rate of a loan, you need to know the loan terms and perform a simple calculation.
Steps
Gather the necessary information
Understand the concept of effective interest rate. The effective interest rate describes the full cost of the loan; it includes the effects of compound interest, which nominal or "stated" interest rates do not account for.
- For example, a loan with a 10% monthly compound interest rate actually has a higher effective interest rate because the interest is compounded monthly.
- The effective interest rate does not include one-time fees, such as loan origination fees. These fees are considered in the annual percentage rate.
Determine the stated interest rate. The stated interest rate (also known as the nominal interest rate) is expressed as a percentage.
- The stated interest rate is typically the "advertised" rate. This is the figure that lenders often use to display their interest rates.
Determine the compounding frequency of the loan. The compounding frequency is usually calculated monthly, quarterly, annually, or continuously. This number represents how often interest is compounded.
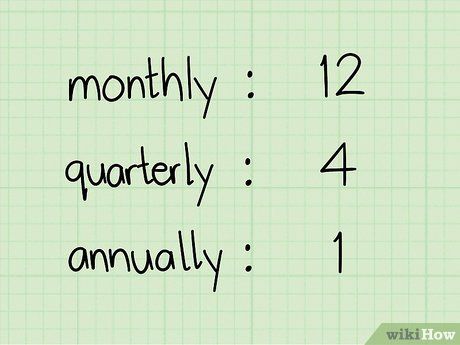
- Typically, interest is compounded monthly. However, it's always a good idea to confirm this with the lender.
Calculate the effective interest rate
Familiarize yourself with the formula for converting the stated interest rate to the effective interest rate. The effective interest rate is calculated using this simple formula: r = (1 + i/n)^n - 1.
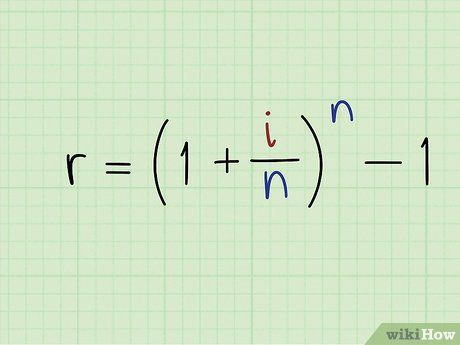
- In this formula, r represents the effective interest rate, i stands for the stated interest rate, and n is the number of compounding periods per year.
Calculate the effective interest rate using the above formula. For example, if a loan has a stated interest rate of 5% and is compounded monthly, using the formula: r = (1 + 0.05/12)^12 - 1, which gives r = 5.12%. If the same loan is compounded daily, the formula becomes: r = (1 + 0.05/365)^365 - 1, resulting in r = 5.13%. Note that the effective interest rate will always be higher than the stated interest rate.
Familiarize yourself with the formula used in continuous compounding scenarios. If interest is compounded continuously, you need to use a different formula to calculate the effective interest rate: r = e^i - 1. In this formula, r represents the effective interest rate, i stands for the stated interest rate, and e is the constant 2.718.
Calculate the effective interest rate in continuous compounding scenarios. For example, consider a loan with a nominal interest rate of 9% and continuous compounding. Using the formula above: r = 2.718^0.09 - 1, which equals 9.417%.
After studying and understanding the theory, you can simplify the calculation as follows.
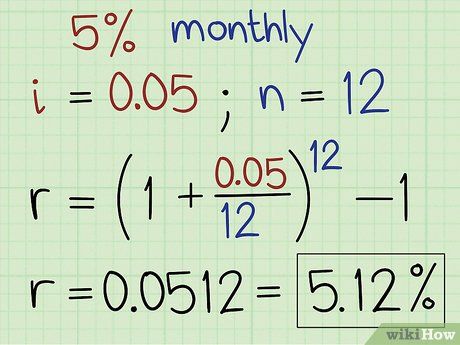
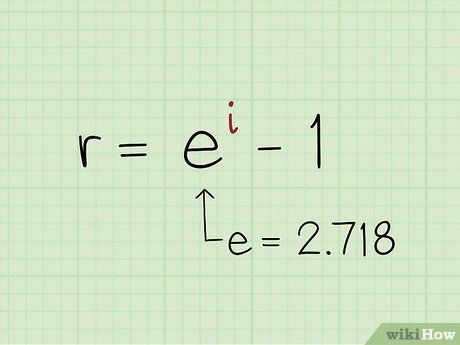
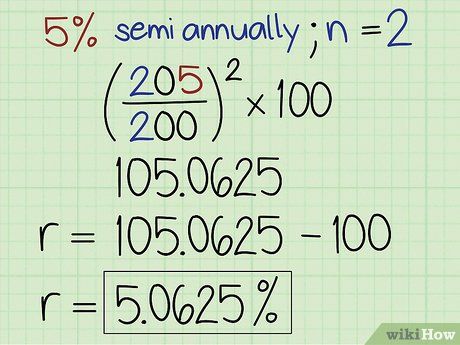
- Once you are familiar with the theory, you can perform the calculation in an alternate way.
- Find the number of periods in a year. The number of periods per year is 2 for semiannual, 4 for quarterly, 12 for monthly, and 365 for daily compounding.
- Multiply the number of periods by 100 and then add the interest rate. For example, if the interest rate is 5%, it will be 205 for semiannual, 405 for quarterly, 1205 for monthly, and 36505 for daily compounding.
- The effective interest is the value exceeding 100 when the principal is 100.
- Perform the following calculations:
- ((205 ÷ 200)^2) × 100 = 105.0625
- ((405 ÷ 400)^4) × 100 = 105.095
- ((1205 ÷ 1200)^12) × 100 = 105.116
- ((36505 ÷ 36500)^365) × 100 = 105.127
- The value above 100 in the case of 'a' is the effective interest rate for semiannual compounding. So, 5.0625 is the effective rate for semiannual, 5.095 for quarterly, 5.116 for monthly, and 5.127 for daily compounding.
- Simply remember the formula as follows:
- (Periods × 100 + Interest Rate) ÷ (Periods × 100) raised to the power of periods, and then multiply the result by 100. The value exceeding 100 is the effective interest rate.
Advice
- There are several online calculators you can use to quickly compute the effective interest rate. Additionally, the EFFECT() function in Microsoft Excel will help you calculate the effective interest rate when you know the nominal rate and the number of compounding periods.
Items You Need
- Pencil
- Paper
- Calculator
