Buzz
A cube is a three-dimensional shape where all three dimensions—width, height, and length—are equal. It has six square faces, and all edges are of the same length and perpendicular to each other. The formula for calculating the volume of a cube is straightforward. Generally, you simply multiply the length × width × height of the cube. Since all edges of a cube are equal in length, another way to express the volume formula is s3, where s represents the length of one side of the cube. See the detailed breakdown of the calculation process in Step 1 below.
Steps
Find the cube root of one side of the cube
Determine the length of one edge of the cube. Usually, when you're tasked with calculating the volume of a cube, the length of one side will be provided. Once you have this measurement, you are ready to compute the cube's volume. If you are not working with a theoretical problem but are instead trying to find the volume of a physical object shaped like a cube, use a ruler or measuring tape to measure the edge.
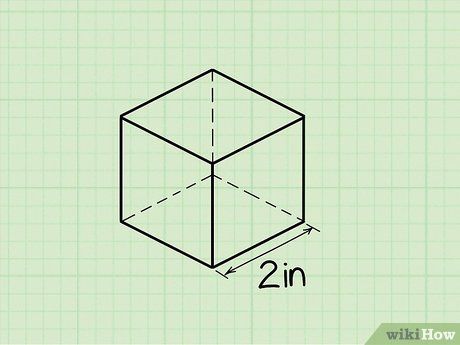
- To better understand the volume calculation, follow each step of the process with the example below. Suppose the length of the side of the cube is 2 cm. We will use this data to find the volume of the cube in the next step.
Cube Volume via Cubing the Side Length. Once you've determined the side length of the cube, the next step is to cube this number. In other words, multiply the number by itself twice. If s represents the side length, the calculation would be s × s × s (or simply s3). This formula will give you the cube's volume!
- This process is similar to finding the area of the base, and then multiplying by the height of the cube (or in other words, length × width × height). Since the length, width, and height of a cube are equal, this method can be simplified by cubing the length of any side.
- Let’s proceed with the example above. If the side length of the cube is 2 cm, we can calculate the volume as 2 x 2 x 2 (or 23) = 8.
Mark your answer with a cubic exponent. Since volume is a three-dimensional measurement, your answer should be in cubic form. In most school math problems, if you don’t write the answer with the correct unit, you'll lose points, so be sure to use the right unit!
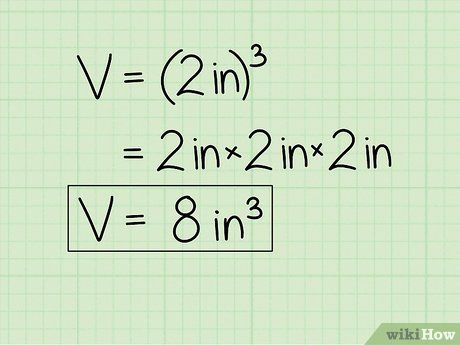
- In our example, since the original measurement is in cm, the final answer should be written in "cubic centimeters" (or cm3). Therefore, our result of 8 will be written as 8 cm3.
- If we had used a different unit of measurement initially, the volume's unit would change accordingly. For example, if our cube had sides of 2 meters, instead of 2 cm, we would use the unit cubic meters (m3).
Calculating Volume from Total Surface Area
Finding the Total Surface Area of a Cube. The easiest way to calculate the volume of a cube is by cubing the side length, but that's not the only method. The length of a cube's side or the area of one of its faces can be derived from other properties of the cube, meaning that if you start with one of these values, you can still calculate the cube’s volume using a slightly longer process. For example, if you know the total surface area of the cube, you can simply divide the total surface area by 6, then take the square root of that result to find the side length. From there, you can cube the side length to find the volume as usual. We will now perform this step-by-step.
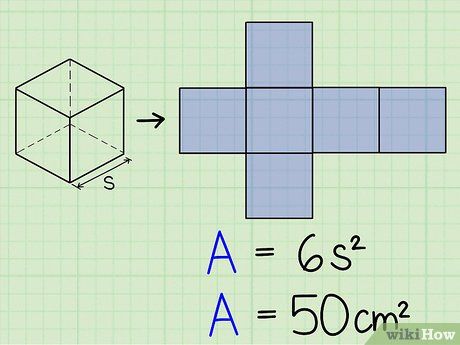
- The total surface area of a cube is calculated with the formula 6s2, where s is the side length of the cube. This formula is essentially the same as calculating the area of each face of the cube (which has six faces) and adding them up. We will use this formula to compute the cube’s volume from its total surface area.
- For example, let’s say we have a cube with a total surface area of 50 cm2, but we don’t yet know the side length. In the following steps, we will use this information to find the cube’s volume.
Divide the Cube’s Total Surface Area by 6. Since a cube has six equal faces, dividing the total surface area by 6 will give you the area of one face. This area is the product of two sides of the cube’s face (length × width, width × height, or height × length).
- In our example, we perform the division 50/6 = 8.33 cm2. Remember, the answer for the area of a face is always in square units (cm2, in2, etc.).
Calculate the square root of this value. The area of a face of a cube is equal to s2 (s × s). The square root of this value will give you the length of the side of the cube. Once you have the side length, you will have all the data you need to calculate the cube's volume as usual.
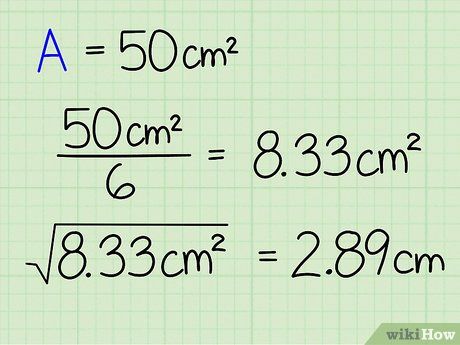
- In our example, √8.33 = 2.89 cm.
Cube the value to find the volume of the cube. Now that you have the length of the cube's side, cube this value (multiply it by itself twice) to find the volume of the cube as explained in the section above. Congratulations! You've determined the volume of the cube based on its total surface area.
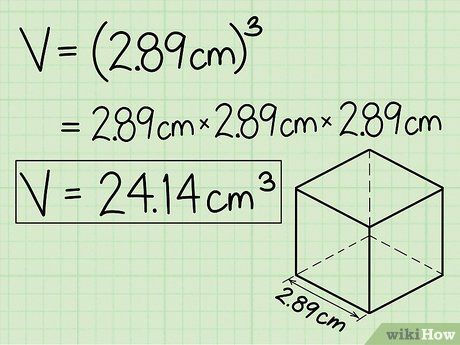
- In our example, 2.89 × 2.89 × 2.89 = 24.14 cm3. Don't forget to note the result in cubic units.
Find the volume from the diagonal
Divide the diagonal of a face of the cube by √2 to find the side length of the cube. In principle, the diagonal of a square face is √2 times the length of one side of the square. Therefore, if all you know is the diagonal of a face of the cube, you can find the side length of the cube by dividing the diagonal by √2. After that, calculating the cube's volume by cubing the side length is relatively simple.
- For example, if a face of the cube has a diagonal of 2.13 meters, we will calculate the side length by dividing 2.13/√2 = 1.51 meters. Now that we know the side length, we can find the volume of the cube by cubing 1.513 = 3.442951 m3.
- Note that, according to the general formula, d2 = 2s2 where d is the diagonal of a face of the cube and s is the side length. This is due to the Pythagorean theorem, where the square of the hypotenuse of a right triangle is the sum of the squares of the other two sides. Since the diagonal of a face of the cube and the two sides form a right triangle, d2 = s2 + s2 = 2s2.
Square the diagonal from two opposite points on the cube, then divide by 3 and find the square root of the result to determine the side length of the cube. If all you know about the cube is the space diagonal from one corner to the opposite corner, you can still find the volume of the cube. Since d becomes one leg of a right triangle with the hypotenuse being the diagonal across the cube, we have D2 = 3s2, where D is the space diagonal connecting two opposite corners of the cube.
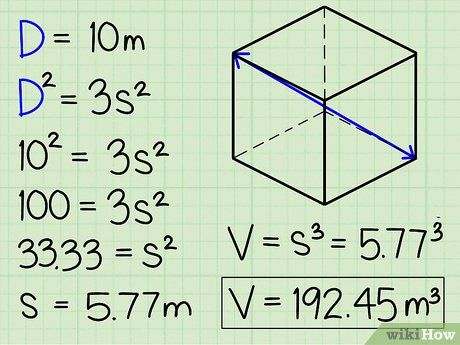
- This formula is derived from the Pythagorean Theorem. D, d, and s form a right triangle with D as the hypotenuse, so we have D2 = d2 + s2. As calculated above, d2 = 2s2, so we get D2 = 2s2 + s2 = 3s2.
- For example, let's say the length of the diagonal from one corner of the cube to the opposite corner on the top face is 10 meters. To calculate the volume, we substitute 10 for "D" in the formula as follows:
- D2 = 3s2.
- 102 = 3s2.
- 100 = 3s2
- 33.33 = s2
- 5.77 m = s. Now, all we need to do to find the volume of the cube is to cube the side length.
- 5.773 = 192.45 m3
