Buzz
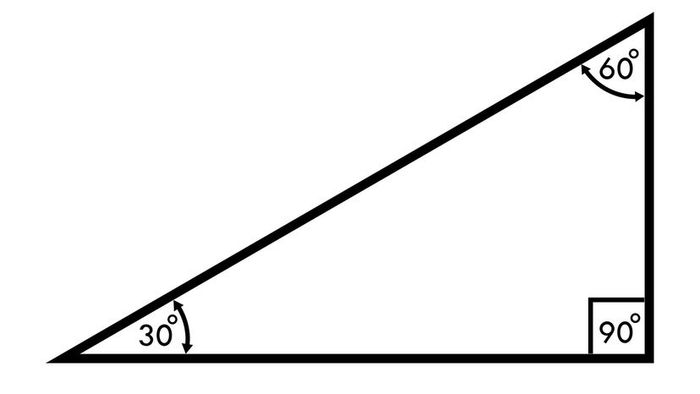
Fortunately, the 30-60-90 triangle is relatively simple. Its largest angle, the 90-degree angle, is always adjacent to the shortest leg and directly opposite the hypotenuse. Image: KRPD / ShutterstockFor anyone who has tackled challenging trigonometry exercises, the Pythagorean Theorem and its square root principles within the 30-60-90 triangle are familiar. This special triangle offers several time-saving rules, enabling budding mathematicians to quickly determine angles and side lengths.
While all triangles have an interior angle sum of 180 degrees, special triangles (like right and equilateral triangles) are the easiest to solve in geometry problems and homework. This is because there is a predictable relationship between angles that maintain the same ratio every time.
Let's examine the theoretical triangle PQR to demonstrate some of the important features of a 30-60-90 triangle.
1. A 30-60-90 Triangle Is Always a Right Triangle
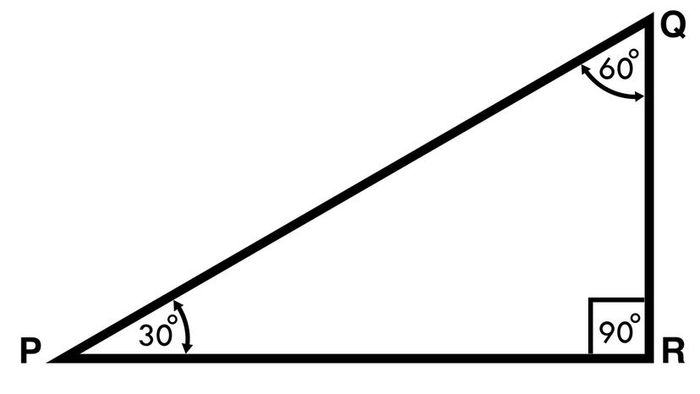Triangle PQR. Image by KRPD / ShutterstockPQR is a unique right triangle. Its sides and angles are not equal, unlike an equilateral triangle where all angles are identical, or an isosceles triangle that has two equal sides.
By cutting an isosceles triangle in half at the angle where the two equal sides meet, you can form two matching right triangles.
2. The Hypotenuse Is Twice the Length of the Smallest Side
If the problem provides the length of one of the two sides (either the hypotenuse, or the shortest side), you can easily determine the length of the other side.
If the problem gives the hypotenuse's length, divide that value by 2 to find the length of the shortest leg. If the shortest leg's measurement is given, multiply it by 2 to find the hypotenuse.
3. The Smallest Angle Is 30 Degrees
In a 30-60-90 triangle, the smallest angle is always 30 degrees, located next to the longest side, the hypotenuse. The other long leg, extending from the 30-degree angle to the right angle, is equal to √3 times the length of the shortest side.
4. The Midsized Angle Is Always 60 Degrees
Keep in mind that the leg of medium length is always opposite the 60-degree angle. Once you identify this angle, you can easily figure out that the other angle must be 30 degrees.
Triangles are frequently used in engineering for structures like roofs, bridges, and other projects that require strong load-bearing capabilities. This is because a triangle distributes weight more effectively than any other shape, while also providing an aesthetically balanced symmetry.
