Buzz
Finding corresponding angles is straightforward once you understand where to look. MytourGeometry is filled with specialized terms that define how various points, lines, surfaces, and other geometric elements relate to each other. Some terms are quite complex, like rhombicosidodecahedron, which we believe might be linked to "Star Trek" wormholes or complex polygons.
At other times, we get simpler terms, such as corresponding angles.
Key Concepts
Before we dive into corresponding angles, let's revisit some fundamental concepts:
- Angle Definition: An angle is formed when two rays meet at a common point. The space between these rays constitutes the angle.
- Parallel Lines: These are two lines on a flat plane that will never meet, no matter how far they extend.
- Transversal Lines: A transversal line is one that crosses at least two other lines, often used as a general term for lines that intersect with others.
Understanding Corresponding Angles: Examples and Insights
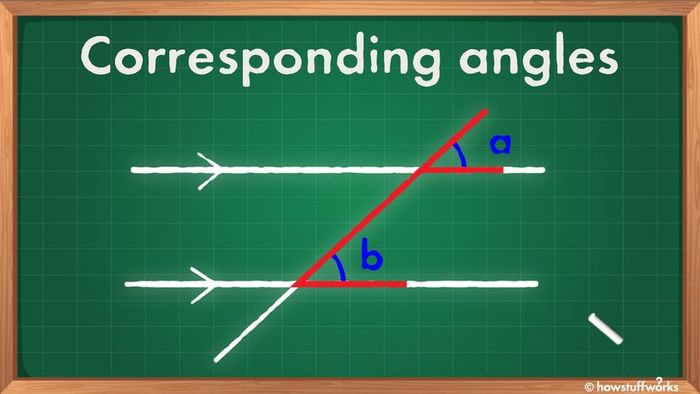
Now, let’s uncover the beauty of corresponding angles. When a transversal cuts through two parallel lines, it forms something remarkable: corresponding angles. These angles are positioned on the same side of the transversal and occupy identical spots across each line it intersects.
Simply put, corresponding angles are congruent, meaning they share the same measurement.
To identify corresponding angles, look for the distinct "F" shape (either forward or backward), marked in red, as seen in the image at the start of the article. In this case, angles labeled "a" and "b" are corresponding angles.
In the main image above, angles "a" and "b" are congruent. You can always identify corresponding angles by spotting the F shape (either forward or backward), highlighted in red. Another example can be found in the image below.
In this diagram, line t represents the transversal line, while lines a and b are parallel. The angles labeled 1 and 5 are corresponding angles, as are 4 and 8, 2 and 6, and 3 and 7. This means their angles are congruent.
Jleedev/Wikimedia Commons/CC BY-SA 3.0John Pauly is a middle school math teacher who uses various methods to help his students understand corresponding angles. He observes that many students find it challenging to identify these angles in diagrams.
For example, he suggests using two similar triangles—triangles that have the same shape but might differ in size. These triangles could have been resized, rotated, or reflected.
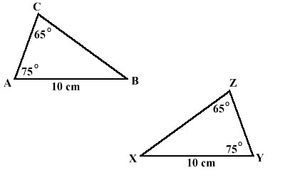Here, we can observe corresponding angles in two triangles. Though the triangles are different, their corresponding angles remain identical.
Isipeoria~enwikibooks/Wikimedia Commons/CC BY-SA 3.0In specific cases, you can make certain assumptions about corresponding angles.
For example, consider two similar figures—figures that have the same shape but may differ in size. If two figures are similar, their corresponding angles are congruent, meaning they are identical. Pauly highlights this as beneficial because it helps the figures maintain their original shape.
He suggests imagining a picture that needs to fit into a document:
Using Corresponding Angles
In real-world scenarios, corresponding angles are very useful. For instance, in projects like constructing railroads, skyscrapers, or other large structures, ensuring parallel lines is essential. One way to verify this is by checking the alignment of corresponding angles.
You can apply the corresponding angles method by drawing a straight line that intersects both lines and then measuring the corresponding angles. If they are congruent, you’ve confirmed the correct alignment.
Importance of Corresponding Angles
Corresponding angles are a key concept in geometry, offering insights into how angles relate when transversal lines intersect parallel lines. Whether you’re passionate about math or want to apply this knowledge practically, mastering corresponding angles can be both informative and useful.
As with most mathematical ideas, students often wonder about the practical applications of corresponding angles. "Well, if you need to verify two parallel lines, you can use this trick," said Pauly. "Simply draw a straight line that cuts across both lines, then measure the corresponding angles." If the angles are congruent, you can be confident that you've correctly measured and aligned the pieces.
