Buzz
We encounter perpendicular lines everywhere in daily life, some that intersect and others that don’t. DALE DE LA REY/Getty ImagesWelders and carpenters rely on various tools to ensure precision when setting things at perfect right angles. A quick glance at any geometry textbook will confirm these are called 'right' angles.
They're everywhere! Many doorframes, windows, carpets, and refrigerator magnets are designed with right angles. To quote 'The Red Green Show,' they’re a handyperson’s best friend.
Right angles are a familiar sight for fans of team sports. Next time your favorite NFL receiver makes a touchdown, take a closer look at the painted field. The four corners of an American football end zone are 90-degree angles, which result from perpendicular lines.
Perpendicular lines intersect at a right angle, setting them apart from parallel lines, which by definition, never cross each other.
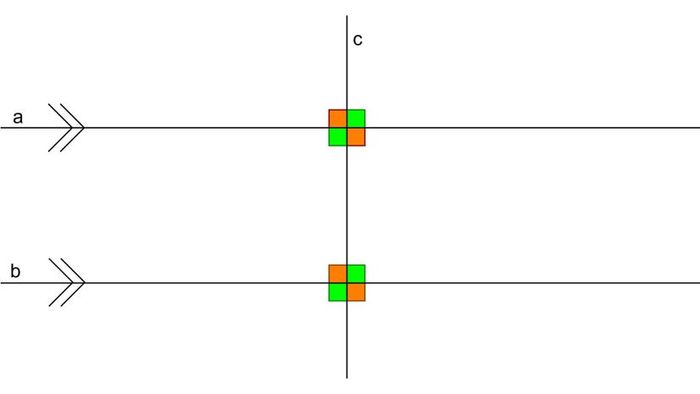Two parallel lines, a and b, are intersected by a perpendicular transversal, c.
Wikimedia Commons (CC BY-SA 3.0)Here’s another key point: perpendicular lines not only intersect at 90-degree angles but also need to be coplanar. The 'co-' prefix gives a clue to this concept. Just like co-workers who share the same workplace, coplanar lines exist on the same plane.
No, this doesn’t mean they booked the same flight. We’re not talking about planes here. A geometric plane is a flat, two-dimensional surface. While it lacks thickness, it stretches infinitely in both length and width.
If you come across two intersecting, coplanar lines and can’t tell if they’re perpendicular, examine their slopes. Essentially, the slope of a line measures how steep it is.
Slopes can be either positive or negative. On graphs, lines with positive slopes rise as you move from left to right above the x-axis, while negative slopes go the opposite direction.
A line that runs parallel to the x-axis is considered to have a zero slope. If one of these 'zero slopers' (not a real math term, but bear with us) crosses a vertical line parallel to the y-axis, voilà! You’ve got perpendicular lines.
Things don’t always work out so neatly. Suppose the intersecting lines don’t align with the x and y axes on the graph. They might still be perpendicular, but only if their slopes are negative reciprocals of each other.
To put it simply, to find the slope of a line, you divide its rise by its run. The rise refers to the vertical distance between two points on a straight line, as measured in the units on your graph. The run, on the other hand, measures the horizontal distance.
By dividing the rise by the run, you get a fraction. 'Negative reciprocals' are just the flipped versions of these fractions. Here's an example to help explain it better:
Let’s say one of our lines — which we’ll call 'Line A' — has a slope of 4/3.
If our other line — 'Line B' — is indeed perpendicular to Line A, we would expect its slope to be -3/4.
Those two slopes are negative reciprocals of each other. In fact, almost all perpendicular lines will have slopes that are negative reciprocals. The only exception is when a line parallel to the y-axis intersects one with a zero slope. That’s just the way it works.
We can also describe slopes as either "high" or "low." A "high" slope refers to one that is extremely steep — like a challenging rock climb. On the other hand, "low" or "shallow" slopes are much more gradual.
