 Sudoku puzzles have gained immense popularity. Peter Dazeley / Getty Images
Sudoku puzzles have gained immense popularity. Peter Dazeley / Getty ImagesIf you’ve visited a bookstore recently — or found yourself in an airport, waiting area, or even a college lecture hall — chances are you’ve noticed someone engrossed in a Sudoku puzzle. Given its widespread appeal, one might mistake it for a modern craze. However, it’s simply a captivating, logic-driven puzzle that’s easy to start but challenging enough to keep you engaged.
In this article, we’ll explore the fundamentals of Sudoku, share strategies for solving it, and uncover its true origins (spoiler: it’s not Japan). Let’s dive in.
Understanding Sudoku Fundamentals
Sudoku, also known as su doku, revolves around numbers — specifically, digits 1 through 9 — but it’s not a math-based game. It’s rooted in logic. The numbers could easily be replaced by the first nine letters of the alphabet or any set of nine symbols, and the essence of the game would remain unchanged.
At its core, the sudoku game is built on a nine-by-nine grid. Players must focus on three key elements: rows, columns, and boxes.
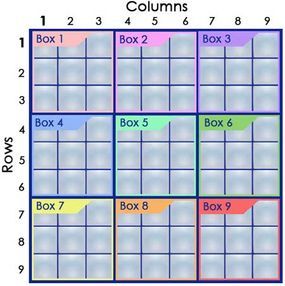
The objective of Sudoku is to populate every nine-square row, column, and box with the numbers 1 through 9, ensuring each digit appears only once in each section. The interplay between rows, columns, and boxes provides clues to determine the correct placement of numbers. For instance, if you began with an empty grid and filled in numbers for row 1, column 2, and box 4 following Sudoku rules, it might resemble this:
Naturally, starting with a completely blank grid wouldn’t be much of a puzzle. A Sudoku challenge comes pre-filled with some numbers, and your task is to deduce the placement of the remaining digits. Here’s an example of an actual Sudoku puzzle from Michael Mepham’s "Book of Sudoku 3":
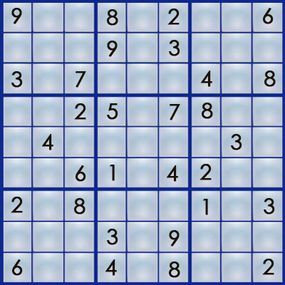 A Sudoku puzzle comes with certain "clues" already filled in.
A Sudoku puzzle comes with certain "clues" already filled in.Sudoku puzzles vary in difficulty, ranging from easy to extremely challenging, depending on the number of starting numbers provided and their placement. (Michael Mepham, the puzzle creator for London's Daily Telegraph, categorizes his puzzles as Gentle, Moderate, Tough, or Diabolical.) An easy puzzle offers sufficient numbers in strategic locations, enabling solvers to use straightforward logic to find the solution. Each puzzle has only one correct answer.
Mastering Sudoku is best achieved by solving puzzles step by step. Let’s explore the easy puzzle above to understand the process. If you can solve an easy puzzle, you can tackle harder ones — it just requires more time and effort.
Sudoku, derived from the mathematical concept of "Latin squares," first appeared as "Number Place" in Dell puzzle books during the 1970s. While it didn’t gain much traction in the U.S., it became a sensation in Japan after its introduction in 1984. Nobuhiko Kanamoto, an editor at Japanese puzzle publisher Nikoli, named it Suuji Wa Dokushin Ni Kagiru ("The Numbers Must be Single"). This was later abbreviated to "sudoku," meaning "single number."
In 1997, New Zealander Wayne Gould stumbled upon Sudoku during a trip to Japan and sought to popularize it in the United States. He developed a computer program to generate puzzles over several years. Although USA Today initially rejected it, the New York Post published it in April 2005.
Solving a Sudoku: Simple Logic
 This puzzle is rated as "gentle" in Michael Mepham's "Book of Sudoku 3."
This puzzle is rated as "gentle" in Michael Mepham's "Book of Sudoku 3."There’s no single correct starting point for a Sudoku puzzle. You could close your eyes, point randomly, and begin there — it’s as valid as any other approach. However, a more strategic starting point is often a row, column, or box that contains the most numbers. Let’s examine the puzzle from the previous page:
Columns 4 and 6 each have six numbers already filled in. We’ll begin with column 4, which already includes the numbers 1, 3, 4, 5, 8, and 9.

To ensure each digit from 1 to 9 appears exactly once, we need to add the missing numbers 2, 6, and 7 to column 4. However, these numbers can’t be placed arbitrarily — each must fit precisely within the puzzle’s solution. To determine their correct positions, we must analyze the rows and boxes intersecting with column 4. Let’s examine the empty square at row 3, column 4 (3,4), along with its corresponding row and box:
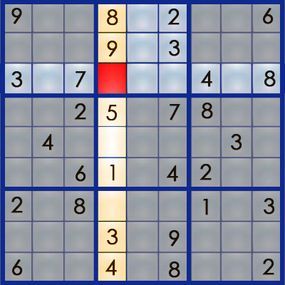 To solve the empty square at row 3, column 4, we’ll need to consider column 4, row 3, and box 2.
To solve the empty square at row 3, column 4, we’ll need to consider column 4, row 3, and box 2.The "simple logic" method for solving Sudoku relies solely on visual inspection and follows this pattern: Can the number 2 fit in the empty square? No, because box 2 already contains a 2, and each number can only appear once per box. Can the 7 fit there? Row 3 already has a 7, so that’s also not possible. This leaves us with the number 6. Since neither row 3 nor box 2 includes a 6, we can confidently place the 6 in that cell. Our first number is solved!

Next, let’s tackle the remaining numbers in column 4, which still needs a 2 and a 7. The empty square at position 5,4 is influenced by row 5 and box 5, while the empty square at 7,4 is influenced by row 7 and box 8.
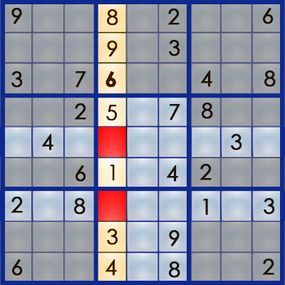
Since box 5 already contains a 7, we can’t place a 7 in the 5,4 square. This means the 2 must go in 5,4, and the 7 must be placed in 7,4:
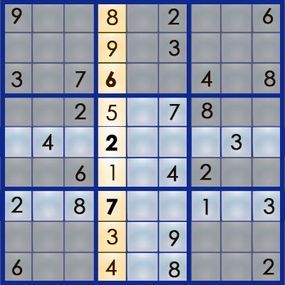
We’ve successfully completed column 4 using only straightforward logic. Given that this is an easy puzzle, much of it can likely be solved this way. However, not all puzzles are this straightforward. For more complex scenarios, we can employ additional strategies, starting with making small pencil marks to track possibilities.
Solving a Sudoku: Possible Numbers
As Sudoku puzzles increase in difficulty, penciling in potential solutions for empty squares becomes essential. However, this isn’t about guessing — it’s about listing possible candidates. Guessing in Sudoku can disrupt the entire puzzle, forcing you to restart, as every number is interconnected.
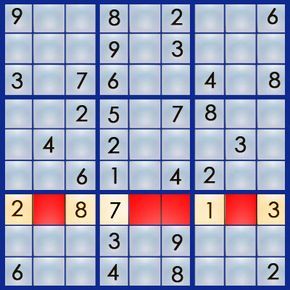
By noting all possible numbers for each empty square in a row, column, or box, we can apply specific strategies to solve the section. Let’s examine row 7, which has four empty squares and requires the numbers 4, 5, 6, and 9.
We’ll pencil in all potential numbers for each empty square. For instance, which of the numbers 4, 5, 6, or 9 could fit in the square at 7,2? The 4 is ruled out because column 2 already contains a 4. The 5 is a possibility since neither row 2 nor box 7 has a 5 yet. The 6 is excluded because box 7 already has a 6. The 9 could fit, as both row 2 and box 7 are missing a 9. Therefore, we’ll pencil in "5 9" for that square:

Applying the same method to the square at 7,5, we eliminate the 4 and 9 (box 8 already has these) and pencil in a 5 and 6. For the square at 7,6, we’ll note a 5 and 6. As for the square at 7,8, any of the numbers could work:
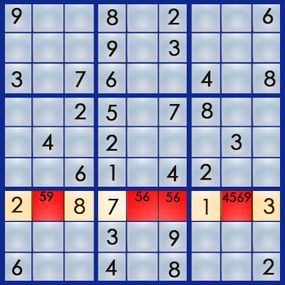
Reviewing the penciled numbers, two observations stand out: First, two squares share the same pair of numbers (and only those two), and second, the number 4 appears only once. Starting with the 4 in square 7,8, we can use the "single occurrence" strategy. Since the 4 can only fit in 7,8, we’ve solved that square, as row 7 requires a 4. Now, row 7 looks like this:
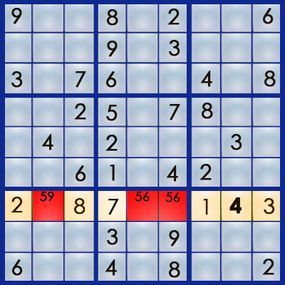
Now, let’s examine the repeating pair: Both 5 and 6 — and only these two numbers — can fit in squares 7,5 and 7,6. This creates a matching pair scenario. The 5 must occupy one of these squares, and the 6 must occupy the other. Using the matching pairs strategy, we can eliminate the 5 from square 7,2, as we know it doesn’t belong there. This solves another square:
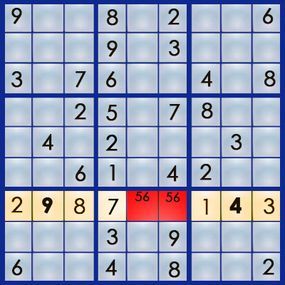
Incidentally, the "matching pairs" elimination strategy also applies to "matching triplets," where three squares share the same trio of numbers, and only those three numbers, in each square.
Based on our penciled notes, we still don’t know which square holds the 5 and which holds the 6, so we’ll continue to explore possibilities. Let’s analyze box 8, which has four empty squares and requires the numbers 1, 2, 5, and 6.
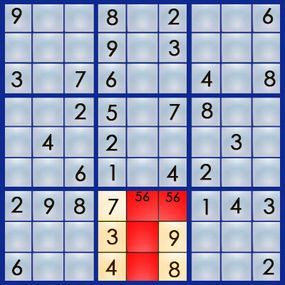
Two of these squares already contain the matching pair of 5 and 6, so we can eliminate these numbers from the other squares. This leaves us with 1 and 2. Either number could fit in square 8,5 — neither row 8 nor column 5 contains a 1 or 2. However, row 9 has a 2, so we can’t place a 2 in square 9,5. Here’s the current state:
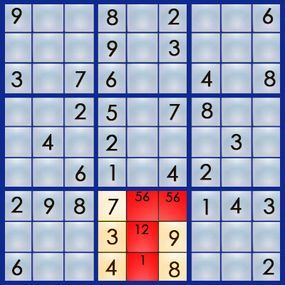
Notice anything? Square 9,5 has only one possible number. Using what Mepham calls the lone number strategy — perhaps the simplest Sudoku tactic — we can confirm that 1 is the solution for 9,5. Since the 1 for box 8 is now placed at 9,5, we can remove the penciled-in 1 from square 8,5, leaving only a 2 — and another solved square.
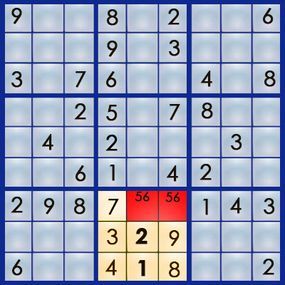
However, the correct positions for the 5 and 6 remain unclear. Solving column 6 will help us determine which number fits in square 7,6. Column 6 has three empty squares, one of which already lists all its possible solutions:
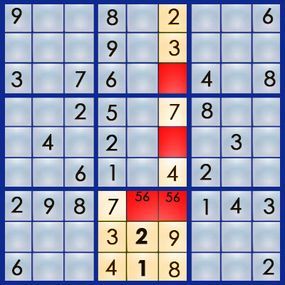
Column 6 requires a 1, a 5, and a 6. For square 3,6, the possible numbers are 1 and 5 (row 3 already contains a 6). For square 5,6, the only viable option is a 6, as box 5 already includes a 1 and a 5.
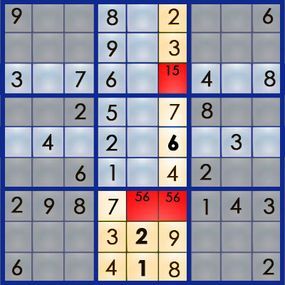
Now we can confirm that the number 5 belongs in square 7,6, the number 1 fits in square 3,6, and the number 6 must be placed in square 7,5.
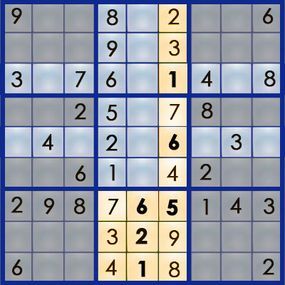
Since the interplay between rows, columns, and boxes is central to Sudoku, solving one square can immediately reveal solutions for five others. So far, we’ve relied on straightforward logic and identified possible numbers for specific squares. In the next section, we’ll adopt a different tactic: identifying possible squares for a given number.
Solving a Sudoku: Possible Squares
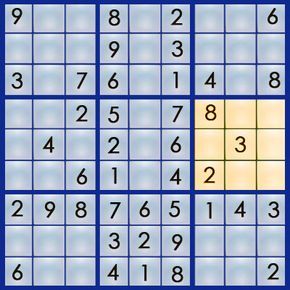
This time, rather than identifying the correct number for a square, we’ll focus on finding the correct square for a specific number. To achieve this, we’ll use a visual elimination method. Let’s examine box 6:
Box 6 is missing a 4. To determine its correct placement, we’ll eliminate all squares where it can’t go. Since there’s a 4 in row 5, we’ll draw a line through that row. Additionally, a 4 exists in row 6 and columns 7 and 8, so we’ll mark those as well.
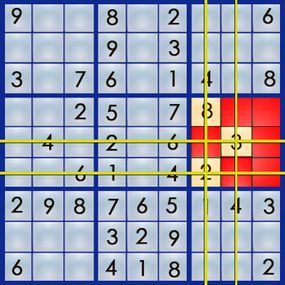
After eliminating these squares, only one open square remains in box 6 — the square at 4,9. We’ve successfully placed the 4.
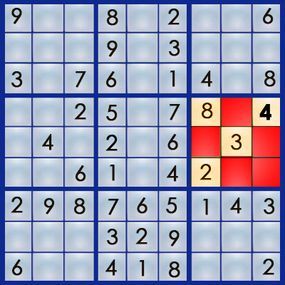
Next, let’s use the same method to locate the 6. By striking through row 5, row 6, and column 9, only one square remains open. We can place the 6 in the square at 4,8.
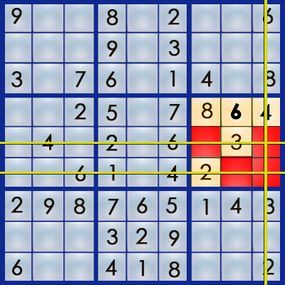
With these strategies, you now have all the tools needed to complete the puzzle on your own!
By applying straightforward logic and the fundamental strategies we’ve covered, along with countless other techniques developed by Sudoku enthusiasts, you’ll be equipped to tackle nearly any Sudoku puzzle. As puzzles grow more challenging, solving each square may take longer, as some squares can’t be resolved until others — or even entire sections of the grid — are completed. With practice, you’ll develop your own unique methods and strategies. It’s all about honing your personal sense of Sudoku logic.
Although Sudoku is rooted in logic, some puzzles eventually defy logical reasoning and, much to the dismay of Sudoku purists, may require guessing.
Solving a Sudoku: Diabolical and Beyond
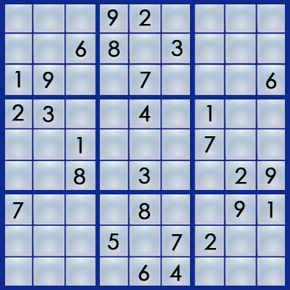
Until recently, some of Michael Mepham’s diabolical-rated Sudoku puzzles in London’s Daily Telegraph couldn’t be solved through logic alone. They required guessing at certain points, a practice frowned upon by Sudoku purists. Due to the backlash (and even hate mail) Mepham received, he stopped publishing puzzles that necessitate guessing. However, solving such puzzles is intriguing, as it demands ensuring no further clues exist before resorting to guessing. Mepham termed this strategy "Ariadne's Thread" (see below), which involves selecting one of two possible numbers for a square and following its implications until reaching a solution or a dead end. If a dead end arises, you backtrack to the guessing point and try the alternative number.
In Michael Mepham’s "Book of Sudoku 3," there’s a diabolical Sudoku puzzle that begins as follows:
By applying logic, you can progress to this point:
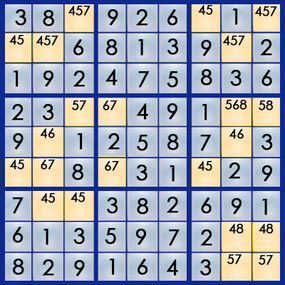
However, we’ve reached a dead end with no further logical clues. The only remaining option is to make an educated guess — keeping our numbers penciled in so we can retrace our steps using Ariadne’s Thread if the guess proves incorrect. If we select a square with only two possible numbers, we have a 50/50 chance of choosing correctly. Let’s choose the 4 in row 2, column 1. Assuming the 4 is correct, we can solve several other squares — but this leads to a contradiction.

If the number 4 is placed at 1,7, then the 5 must go at 6,7. However, row 6 already contains a 5. This means our initial guess was wrong, and we must erase the derived solutions, returning to square 2,1. This time, we’ll choose the 5.
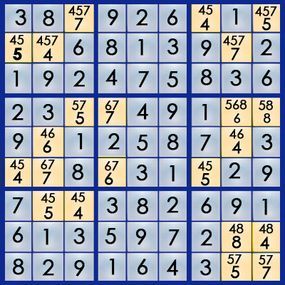
The 5 is indeed the correct solution for square 2,1, enabling us to complete the entire puzzle.
Although Mepham no longer publishes Sudoku puzzles that require guessing in his column, you can still find them on his Sudoku website, sudoku.org.uk.
Due to Sudoku’s immense popularity, various versions of the puzzle have emerged to offer even greater challenges. One such variant is 3-D Sudoku. This involves arranging nine complete Sudoku grids into a three-dimensional cube, requiring complete rows, columns, and boxes across three interconnected axes. The same rules apply, but now you’re solving across multiple planes. To solve the cube, each of the nine grids must be tackled individually. Alternatively, you can use one of the many 3-D Sudoku computer programs to experience the puzzle in full three-dimensional detail.
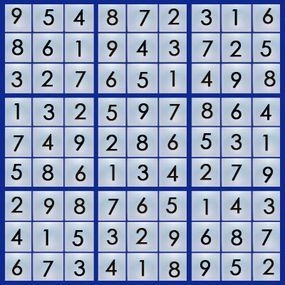
Puzzle Answer from Previous Page
In Greek mythology, King Minos of Crete demands human sacrifices for the monster residing in his labyrinth. The young warrior Theseus vows to slay the beast, and Ariadne, the King’s daughter, falls in love with him. She devises a foolproof plan for Theseus to escape the maze after killing the monster: Theseus will lay a thread along his path into the labyrinth. If he encounters a dead end, he’ll retrace his steps using the thread and choose a new route. By the time he reaches the monster, he’ll have a clear trail of thread guiding him back to safety.
