 Fred Beasley of the 49ers sprinting with the ball. Explore more football visuals.
Photo courtesy San Francisco 49ers
Fred Beasley of the 49ers sprinting with the ball. Explore more football visuals.
Photo courtesy San Francisco 49ersTossing a football to a friend involves applying principles of physics. You instinctively account for variables like distance, wind speed, and the ball's weight. The greater the distance, the more force or higher angle you need to use. These calculations happen automatically in your mind, demonstrating physics in action, even if you don’t consciously label it as such.
Physics is the scientific field that examines the natural world. In football, the most applicable area is mechanics, which focuses on motion and the forces behind it. We’ll explore three key types of motion relevant to the sport:
- Throwing a football through the air
- Players moving across the field
- Halting advancing players
A weekend football game offers more than just insights into passing stats or yardage gains. It’s a live demonstration of fundamental physics principles, evident in the ball’s trajectory, player movements, and the impact of tackles. This article explores how physics shapes the game of football.
Throwing the Football
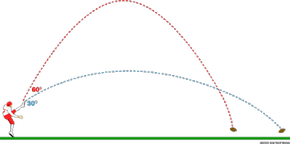 The distance a kick covers is influenced by its angle.
The distance a kick covers is influenced by its angle.A football in flight follows a curved, or parabolic, trajectory due to the effect of gravity on its vertical motion. As the ball rises, gravity decelerates it until it momentarily pauses at its highest point. Then, as it descends, gravity accelerates it until it lands. This pattern, known as projectile motion, applies to any object launched into the air, such as a football, arrow, or missile. To understand this concept in football, let’s analyze a punt (Figure 1). A punter can manipulate three key factors when kicking the ball:
- The speed at which the ball is launched from the foot
- The angle of the kick
- The spin imparted on the football
The ball's rotation—whether spiral or end-over-end—affects its deceleration in flight due to air resistance. A spiraling kick encounters less air drag, maintains speed better, stays airborne longer, and travels farther compared to an end-over-end kick. The ball's velocity and the kick's angle are the primary factors influencing:
- The duration the ball stays airborne (hang-time)
- The maximum height the ball reaches
- The total distance the ball travels
When the punter kicks the ball, it moves with a specific velocity (speed combined with direction) determined by the force applied. The ball travels in both horizontal and vertical directions. Since the ball is launched at an angle, its velocity splits into horizontal and vertical components. The angle of the kick dictates the speed in each direction. A steep angle results in greater vertical velocity, causing the ball to soar high with long hang-time but limited distance. Conversely, a shallow angle increases horizontal velocity, producing a low, short hang-time kick that covers more ground. The punter must choose the optimal angle based on field position. These principles also apply to passes and field goals, though field goal kickers face added challenges as the ball often peaks before reaching the goalposts.
If you prefer to skip the calculations for hang-time, peak height, and punt range, click here to proceed.
- Acceleration - Rate of change of velocity over time (calculated by subtracting initial velocity from final velocity and dividing by the time taken)
- Force - An influence that alters an object's speed or direction
- Velocity - The speed and direction of an object's movement (distance divided by time)
- Speed - The rate at which an object moves (distance divided by time)
Since physics is a quantitative science, establishing units and measurements helps in understanding its impact on football. Here are some useful figures and units developed by Dr. David Haase of North Carolina State University:
- Player at full speed - ~22 miles per hour (9.8 m/s)
- Linebacker - ~220 pounds (98 kg)
- Offensive lineman - ~300 pounds (133 kg)
Punting: Hang-Time, Peak Height and Range
The trajectory of a football follows a parabolic curve, which can be expressed using these two equations:
y = Vyt - 0.5gt2
y = Vyt - 0.5gt
x =Vxt
x =Vxt
- y represents the height at any given time (t)
- Vy denotes the vertical component of the football's initial velocity
- g is the acceleration due to gravity, 9.8 m/s²
- x indicates the horizontal distance of the ball at any time (t)
- Vx signifies the horizontal component of the football's initial velocity
To determine the hang-time (ttotal), peak height (ymax), and maximum range (xmax) of a punt, you need the initial velocity (V) of the ball as it leaves the kicker's foot and the angle (theta) of the kick.
The velocity must be divided into horizontal (Vx) and vertical (Vy) components using these formulas:
- Vx = V cos(theta)
- Vy = V sin(theta)
The hang-time (ttotal) can be calculated using one of the following two formulas:
- ttotal = (2Vy/g)
- ttotal = (0.204Vy)
Once the hang-time is known, the maximum range (xmax) can be determined:
- xmax = Vx ttotal
The time (t1/2) at which the ball reaches its peak height can be calculated as follows:
- t1/2 = 0.5 ttotal
The peak height (ymax) can be calculated using one of these two formulas:
- ymax= vy(t1/2) - 1/2g(t1/2)
- ymax = vy(t1/2) - 0.49(t1/2)
For instance, a kick with a velocity of 90 ft/s (27.4 m/s) at a 30-degree angle will yield the following values:
Vertical and horizontal velocity components:
- Vx = V cos(theta) = (27.4 m/s) cos (30 degrees) = (27.4 m/s) (0.87) = 23.7 m/s
- Vy = V sin(theta) = (27.4 m/s) sin (30 degrees) = (27.4 m/s) (0.5) = 13.7 m/s
Hang-time:
- ttotal = (0.204Vy) = {0.204 (13.7 m/s)} = 2.80 s.
Maximum range:
- xmax = Vx ttotal = (23.7 m/s)(2.80 s) = 66.4 m
- 1 m = 1.09 yd
- xmax = 72 yd
Time at peak height:
- t1/2 = 0.5 ttotal = (0.5)(2.80 s) = 1.40 s
Peak height:
- ymax = Vy(t1/2) - 0.49(t1/2)= [{(13.7 m/s)(1.40 s)} - {0.49(1.40 s)}] = 18.2 m
- 1 m = 3.28 ft
- ymax = 59.7 ft
Calculating for a punt with the same velocity but at a 45-degree angle yields a hang-time of 3.96 s, a maximum range of 76.8 m (84 yd), and a peak height of 36.5 m (120 ft). At a 60-degree angle, the hang-time increases to 4.84 s, the maximum range drops to 66.3 m (72 yd), and the peak height rises to 54.5 m (179 ft). As the kick angle steepens, the ball stays airborne longer and reaches greater heights. Additionally, the distance peaks at 45 degrees before decreasing with steeper angles.
Runners on the Field
Analyzing runners on the field involves considering several key factors:
- Their starting positions for a play
- Their ability to change directions
- Their movement in open space
Line-Up Positions
Observing the backs, both offensive and defensive, we notice they usually position themselves away from the line of scrimmage, flanking the linemen. This setup provides them with the space and time needed to accelerate from a standstill to top speed, whether they are carrying the ball or chasing the ball carrier. Notably, linebackers have more room to accelerate than linemen, and wide receivers have even more space than linebackers. As a result, linebackers can achieve higher speeds than linemen, while wide receivers can reach the fastest speeds overall.
Changing Directions on the Field
Consider a running play where the quarterback hands the ball to a running back. Initially, the running back is stationary in the set position. Upon receiving the ball, he accelerates to his top speed of 22 mi/h (9.8 m/s) within 2 seconds. His acceleration (a) is calculated as:
a = (vf - vo)/(tf - to)
a = (vf - vo)/(tf - to)
- vf represents final velocity
- vo represents initial velocity
- tf represents final time
- to represents initial time
a=(9.8 m/s - 0 m/s)/(2 s - 0 s)
a= 4.9 m/s
While running with the play's flow (e.g., to the right), he maintains a steady speed (a = 0). Upon spotting an opening, he plants his foot to halt his rightward motion, changes direction, and accelerates upfield into the gap. By planting his foot, he exerts a force on the turf, which serves two purposes:
- Halting his rightward motion
- Propelling him upfield
Stopping his rightward motion involves two forces. First, the force he applies to the turf by planting his foot. Second, the friction between his foot and the turf. Friction plays a crucial role in enabling runners to change direction. If you've ever watched a football game in the rain, you've seen how runners struggle when friction is minimal. Here's what happens when a runner attempts to change direction on a wet surface:
- When he plants his foot to decelerate, the coefficient of friction between the turf and his foot decreases due to the water on the surface.
- The lower coefficient of friction reduces the frictional force.
- The diminished frictional force makes it difficult for him to halt his rightward motion.
- The runner slips and falls.
The combined force he applies and the frictional force must halt his rightward motion. Assuming he stops in 0.5 seconds, his acceleration must be:
- a = (0 m/s - 9.8 m/s)/(0.5 s - 0 s)
- a = -19.6 m/s
*The negative sign indicates that the runner is accelerating in the opposite direction, to the left.
The force (F) needed to stop him is calculated by multiplying his mass (m), estimated at 98 kg (220 lbs), by his acceleration:
- F = ma = (98 kg)(-19.6 m/s) = 1921 Newtons (N)
- 4.4 N = 1 lb
- F = ~500 lbs!
To accelerate upfield, he exerts force against the turf, and the turf responds with an equal and opposite force, propelling him forward. This demonstrates Isaac Newton's third law of motion, which states that "for every action, there is an equal and opposite reaction." If he accelerates to full speed in 0.5 seconds, the turf applies 1921 N, or roughly 500 lbs, of force. If no one obstructs his path, he will achieve and maintain top speed until he either scores or is tackled.
Running in an Open Field
In an open field, a player can achieve maximum momentum. Since momentum is the product of mass and velocity, players of different masses can have identical momentum. For instance, our running back's momentum (p) would be:
- p = mv = (98 kg)(9.8 m/s) = 960 kg-m/s
For a 125 kg (275 lb) lineman to match this momentum, he would need to move at a speed of 7.7 m/s. Momentum plays a crucial role in stopping (tackling or blocking) runners on the field.
- Mass - The quantity of matter in an object
- Momentum - The product of an object's mass and its velocity
- Impulse - The product of force and the duration over which it is applied
Blocking and Tackling
 Players apply physics principles to stop opponents on the football field.
Photo courtesy North Carolina State University
Players apply physics principles to stop opponents on the football field.
Photo courtesy North Carolina State UniversityTackling and blocking runners depend on three key physics principles:
- Impulse
- Conservation of momentum
- Rotational motion
When Runner and Tackler Collide
While our running back moves across the open field, he possesses a momentum of 960 kg-m/s. To halt his progress—alter his momentum—a tackler must apply an impulse in the opposite direction. Impulse is the result of the force applied multiplied by the duration of its application. Since impulse, like momentum, is a product, the same impulse can be achieved by adjusting either the force or the contact time. If a defensive back aims to tackle our running back, he must apply an impulse of 960 kg-m/s. If the tackle happens in 0.5 seconds, the required force would be:
F = impulse/t = (960 kg-m/s)/(0.5 s) = 1921 N = 423 lb
On the other hand, if the defensive back extends the contact time with the running back, he could reduce the force needed to stop him.
In any collision or tackle where no external forces are involved, the total momentum of the participants remains constant before and after the collision—this is the principle of conservation of momentum. Let's examine three scenarios:
- The ball carrier and tackler possess equal momentum.
- The ball carrier has greater momentum than the tackler.
- The ball carrier has less momentum than the tackler.
For this analysis, we'll assume an elastic collision, where the players do not remain connected after impact.
- If the ball carrier and tackler have equal momentum, the ball carrier's forward momentum is counteracted by the tackler's backward momentum. Both players will stop moving at the point of contact.
- If the ball carrier has more momentum than the tackler, he will push the tackler backward with momentum equal to the difference between them, likely breaking the tackle. After breaking free, the ball carrier will accelerate.
- If the ball carrier has less momentum than the tackler, he will be driven backward with momentum equal to the difference between the two players.
In many cases, tacklers attempt to hold onto the ball carrier, causing the two to move together. In these inelastic collisions, the outcomes are similar to those above, but in scenarios 2 and 3, the speed at which the combined players move forward or backward is reduced. This reduction occurs because the momentum difference is now spread across the combined mass of both players, rather than just the player with less momentum.
- Center of mass - The point where a body's mass is considered to be concentrated.
- Torque - A force that causes rotation or twisting
The Tackling Process
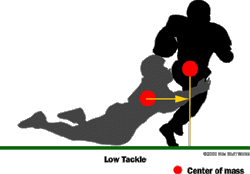
Coaches frequently instruct players to tackle a runner low. This technique causes the runner's feet to rotate in the air toward the direction of the tackle. Let's examine this in detail:
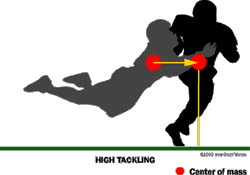
Visualize the runner's mass concentrated at a single point called the center of mass. In men, this point is typically at or slightly above the navel, while in women, it is usually lower, closer to the hips. Objects rotate most easily around their center of mass. Therefore, applying force on either side of the center of mass causes rotation. This rotational force is known as torque, which is the product of the force applied and the distance from the center of mass. Since torque is a product, the same rotational effect can be achieved at different distances by adjusting the force: less force is needed farther from the center of mass. Thus, tackling a runner low—far from the center of mass—requires less force than tackling high. Additionally, if a runner is hit directly at the center of mass, he won't rotate but will be driven in the direction of the tackle.
 A lineman crouches low to position his center of mass closer to the ground, making it difficult for an opponent to move him.
A lineman crouches low to position his center of mass closer to the ground, making it difficult for an opponent to move him.Similarly, coaches frequently instruct linemen to maintain a low stance. This positions their center of mass closer to the ground, ensuring that an opponent, regardless of how low they go, can only make contact near their center of mass. This strategy makes it challenging for an opposing player to move them, as they won't rotate upon impact. This approach is especially crucial for defensive linemen protecting their goal in the "red" zone, the final 10 yards before the goal line.
We've only scratched the surface of how physics applies to football. Keep in mind, this understanding often feels instinctive; players and coaches rarely consciously apply physics principles to their gameplay. However, by making these connections, we gain a deeper appreciation for the incredible physical feats seen on the field. Additionally, applying physics to football enhances equipment safety, influences game rules, boosts athletic performance, and deepens our connection to the sport.
Special thanks to Dr. David Haase, professor of physics and director of The Science House at North Carolina State University in Raleigh, NC.
