 While it may appear straightforward, arranging eight queens on a single chessboard without conflicts is more challenging than it seems.
©iStockphoto.com/Thinkstock
While it may appear straightforward, arranging eight queens on a single chessboard without conflicts is more challenging than it seems.
©iStockphoto.com/ThinkstockDepending on your social circle—perhaps your closest friend is a computer programmer and your sibling is a chess genius—you might already know about the 8 Queens puzzle. For others, this puzzle (also referred to as the 8 Queens problem or simply "8 Queens") isn’t typically a topic of daily contemplation.
The challenge is straightforward: How can you position eight queens on a chessboard without any two threatening each other? Sometimes, the puzzle is framed as, "What’s the highest number of queens that can be placed on a chessboard without mutual attacks?" However, this version becomes less daunting once you Google it and encounter the term "the 8 Queens puzzle."
You might wonder why anyone would care about the placement of eight queens. On the surface, it’s just a strategic challenge. However, as any programmer friend would tell you, the 8 Queens puzzle serves as an excellent test of a coder’s ingenuity and skill.
Don’t worry—you won’t need to dive into the complexities of coding to continue. However, it’s worth noting that solving this puzzle often involves writing a program. Some solutions are more efficient than others. For example, a basic "brute-force" approach might check every possible arrangement, eliminating invalid ones. In contrast, a skilled programmer can craft a more elegant solution using a refined algorithm, finding answers much quicker. This puzzle is a fantastic way to assess a coder’s creativity and problem-solving abilities.
While we won’t bombard you with binary code to explain the 8 Queens puzzle, we will provide you with a few solutions to the problem.
Origin and Explanation of 8 Queens Puzzle
Now that we understand the puzzle’s basic concept, let’s explore what makes it so unique. To do this, let’s revisit some chess fundamentals. In chess, the queen is the most powerful piece, capable of moving any number of squares vertically, horizontally, or diagonally. The only limitation is that she cannot jump over other pieces—if a pawn blocks her path, she must capture it and stop there.
This is what makes the 8 Queens puzzle so intriguing. Given that queens can move vertically, horizontally, and diagonally, how many queens can coexist on a chessboard without threatening each other? You might think to experiment by placing queens randomly, testing various combinations until you find a solution. While this is feasible, there are 4,426,165,368 possible arrangements, so finding a more efficient method is advisable.
Before exploring billions of potential queen placements, let’s credit the person who first conceived this puzzle. Unsurprisingly, it wasn’t someone binge-watching TV shows—it was Max Bezzel, a 19th-century German chess master and composer. (A chess composer creates chess problems or puzzles.) The puzzle debuted in the German chess magazine Die Schachzeitung in 1848.
Bezzel wasn’t focused on solving the puzzle; he simply posed the question. However, in 1850, mathematician Franz Nauck addressed the problem in an article, eventually becoming the first to solve it. This caught the attention of Karl Gauss, a renowned 19th-century mathematician famous for his contributions to algebra. Gauss’s interest spurred others to explore the puzzle, leading to various innovative solutions.
Solutions to 8 Queens
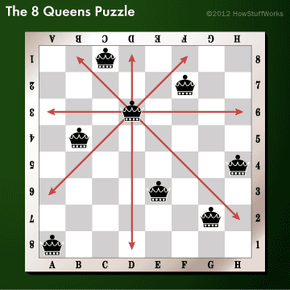 Here’s one possible solution to the 8 Queens puzzle.
Lee Dempsey/Mytour.com
Here’s one possible solution to the 8 Queens puzzle.
Lee Dempsey/Mytour.comUnsurprisingly, the answer to how many queens can coexist on a chessboard without threatening each other is "eight." However, let’s delve into how many distinct arrangements are possible and how this number is determined.
While brute-force computer programs can solve the puzzle—and manually testing 4,426,165,368 possibilities certainly counts as brute force—there are more efficient methods. One such approach was introduced by mathematician J.W.L. Glaisher in 1874. He used determinants to simplify the problem, constructing a matrix and deriving a system that reduced the possible solutions to 92.
The total number of solutions remains 92. However, don’t be misled—you can’t simply set up 92 unique chessboards with peaceful queens. In reality, there are only 12 truly distinct solutions.
Confused? The distinction between 12 unique solutions and 92 fundamental ones lies in perspective. While you can arrange 12 unique boards with eight queens, rotating or reflecting the board can create technically "different" solutions. (This is known as rotational and reflective symmetry operations.) By rotating the board 90, 180, and 270 degrees and reflecting it at each angle, you generate variations. However, one unique board is symmetrical, appearing identical from two angles. While most boards have eight variants, this symmetrical one has only four. Thus, instead of 12 boards multiplied by 8 variations (96), we subtract the four nonexistent variants, resulting in 92 fundamental solutions.
Don’t let the math intimidate you. You can always grab a chessboard and try to figure out some placements on your own. (Finding one solution is much simpler than uncovering all 12.) There are also online Web programs that help you explore different solutions. (Warning: they might make you question your intelligence.)
Before you start rearranging your queens, head to the next page for more insights.
Author's Note
As someone more drawn to words than algorithms, I initially doubted my ability to grasp the 8 Queens puzzle. While I assumed it had practical uses, I couldn’t quite see them. Ironically, it was realizing the sheer scale of the problem that made its utility clear. Solving such a complex puzzle from countless possibilities is precisely why coding exists. The 8 Queens challenge pushes programmers and mathematicians to develop innovative methods for simplifying complex searches.
Related Links
- How Cryptograms Work
- How Cryptoquotes Work
- How to Play Numbrix
- How Chess Puzzles Work
Sources
- Alfed, Peter. "The N by N Queens Problem." University of Utah, Department of Mathematics. Sept. 03, 1997. (June 6, 2012) http://www.math.utah.edu/~alfeld/queens/queens.html
- Ball, Walter William Rouse. "Mathematical Recreations and Essays." Macmillan. 1919. (June, 6, 2012) http://books.google.com/books?id=hvDuAAAAMAAJ&pg=PA113&lpg=PA113&dq=franz+nauck&source=bl&ots=p3cbvU0VSQ&sig=2YOi6HdSBTv42PD74MHzY3QPBSw&hl=en&sa=X&ei=wd3OT-uoOYSG2gWZwtjFDA&ved=0CFYQ6AEwAw#v=onepage&q=franz%20nauck&f=false
- Becher, Michael. "The 8 Queens Problem." 2011. (June 6, 2012) http://www.eightqueen.becher-sundstroem.de/index.php
- Chatham, Doug. "The N+k Queens Problem Page." Morehead State University. Nov. 30, 2011. (June 6, 2012) http://people.moreheadstate.edu/fs/d.chatham/nkqueens.html
- Dealy, Sheldon. "Common Search Strategies and Heuristics with Respect to the N-Queens Problem." University of New Mexico Department of Computer Science. (June 6, 2012) http://www.cs.unm.edu/~sdealy/nqueens_presentation.pdf
- Dealy, Sheldon. "Common Search Strategies and Heuristics With Respect to the N-Queens Problem." University of New Mexico Department of Computer Science. Dec. 10, 2004. (June 6, 2012) http://www.cs.unm.edu/~sdealy/nqueens_proj.pdf
- Edwards, Jon. "Chess is Fun." Princeton University. (June 6, 2012) http://www.princeton.edu/~jedwards/cif/intro.html
- Glaisher, J.W.L. "Glaisher on the problems of the eight queens." Philosophical Magazine and Journal of Science. July-Dec. 1874. (June 6, 2012) http://books.google.com/books?id=nKxSCc5_cCcC&pg=PA457&lpg=PA457&dq=glaisher%20on%20the%20problem%20of%20the%20eight%20queens&source=bl&ots=3FsFz-lPDF&sig=66bdEtWGsZQy3jkzcR3VDgQEOyU&hl=en&ei=8Jl-TuijA4nWiALumYCYCQ&sa=X&oi=book_result&ct=result&resnum=2&ved=0CCYQ6AEwAQ#v=onepage&q=glaisher%20on%20the%20problem%20of%20the%20eight%20queens&f=false
- Godden, Kurt. "Eight Lonely Queens." Chess.com Blog. June 21, 2008. (June 6, 2012) http://blog.chess.com/kurtgodden/8-lonely-queens
- Hoffman, E.J., et al. "Constructions for the Solutions of the m Queens Problem." Mathematics Magazine. Vol. 42, no. 2. 66-72. March 1969. (June 6, 2012) http://penguin.ewu.edu/~trolfe/QueenLasVegas/Hoffman.pdf
- Schachclub Ansbach. "Max Frederick Wilhelm Bezzel (translated from German)." (June 6, 2012) http://www.schachclub-ansbach.de/chronik_bezzel.htm
- Shah, Karan. "8 Queens Problem (1st Lab)." Algorithm Lectures. Jan. 5, 2010. (June 6, 2012) http://bvmalgolectures.blogspot.com/2010/01/8-queens-problem1st-lab.html
- Spivey, Mike. "Solving n-Queens with determinants." Mathematics - StackExchange.com. Sept. 25, 2011. (June 6, 2012) http://math.stackexchange.com/questions/67236/solving-n-queens-with-determinants
- The Chess Store. "Rules for Playing Chess." 2012. (June 6, 2012) http://www.thechessstore.com/category/rulesofchess/
- Wall, Bill. "Great Chess Composers." Chess.com. Aug. 7, 2007. (June 6, 2012) http://www.chess.com/article/view/great-chess-composers
- Weisstein, Eric W. "Gauss, Karl Friedrich." Eric Weisstein's World of Science. 2007. (June 6, 2012) http://scienceworld.wolfram.com/biography/Gauss.html
- Weisstein, Eric W. "Queens Problem." From MathWorld--A Wolfram Web Resource. (June 6, 2012) http://mathworld.wolfram.com/QueensProblem.html
