Buzz
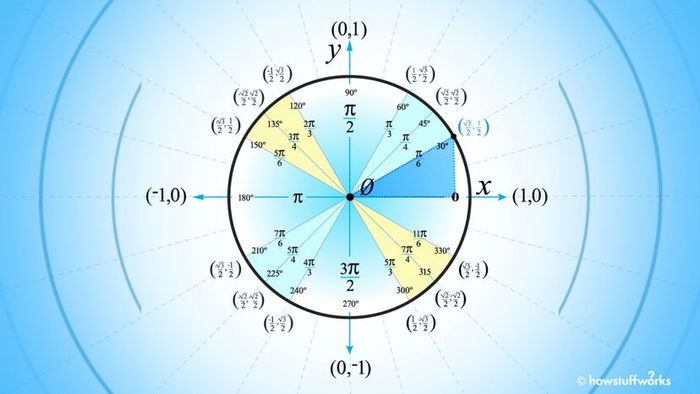
The unit circle is fundamental in defining trigonometric functions such as sine, cosine, and tangent, which describe relationships within right triangles. © Mytour 2021Most people have a basic understanding of what a circle looks like—think of a basketball hoop, a car wheel, or a coin. From geometry, you might recall that the radius is a straight line extending from the center of the circle to its edge.
A unit circle is simply a circle with a radius of 1. However, it often includes additional features that make it a powerful tool in mathematics.
Why Is the Unit Circle Important?
Fig. 1. A unit circle. Radius = 1.
© Mytour 2021The unit circle establishes the relationships of sine, cosine, and tangent in right triangles, illustrating how angles and sides are interconnected.
Consider a right triangle with a 30-degree angle and a hypotenuse measuring 7 units. Using the principles of trigonometric relationships, we can determine the lengths of the other two sides.
Trigonometry, this essential branch of mathematics, finds its use in various real-world applications such as construction, GPS navigation, plumbing, video game development, engineering, carpentry, and aviation.
Memorizing a standard unit circle requires familiarity with three key elements:
- Four quadrants
- 16 angles
- (x, y) coordinates for each of the 16 angles, where the radius intersects the circle's edge
To make this easier, let's imagine a visit to the Unit Pizza Palace. Spend a moment committing the following to memory until you can recall it effortlessly:
- 4 pizza slices
- 3 pies for $6
- 2 square tables
- 1, 2, 3
Step 1: 4 Pizza Slices
Picture a full pizza divided into four equal slices. In mathematical terms, these four sections are referred to as quadrants.
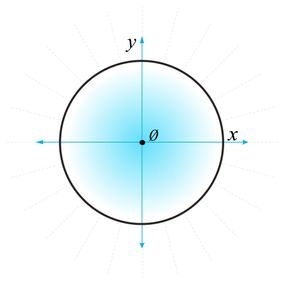Fig. 2. Unit circle with quadrants labeled. The top right is the first quadrant, the top left is the second, the bottom left is the third, and the bottom right is the fourth.
© Mytour 2021Any point on the circle's circumference can be described using (x, y) coordinates. The x-coordinate indicates horizontal movement from the center, while the y-coordinate represents vertical movement.
The x-coordinate represents the cosine of the angle created by the point, the origin, and the x-axis, while the y-coordinate matches the sine function's value for that same angle.
In a unit circle, a line extending rightward from the center will intersect the circle's edge at (1, 0). If the line moves in other directions, the coordinates are as follows:
- Left: (-1, 0)
- Up: (0, 1)
- Down: (0, -1)
The four corresponding angles, measured in radians (not degrees), all share a denominator of 2. (A radian is the angle formed by wrapping the radius around the circle, while a degree measures angles based on distance traveled. A full circle is 360 degrees or 2π radians.)
Starting at the coordinate (1, 0), the numerators begin at 0 and increase counterclockwise by 1π, resulting in 0π/2, 1π/2, 2π/2, and 3π/2. Simplifying these fractions gives 0, π/2, π, and 3π/2.
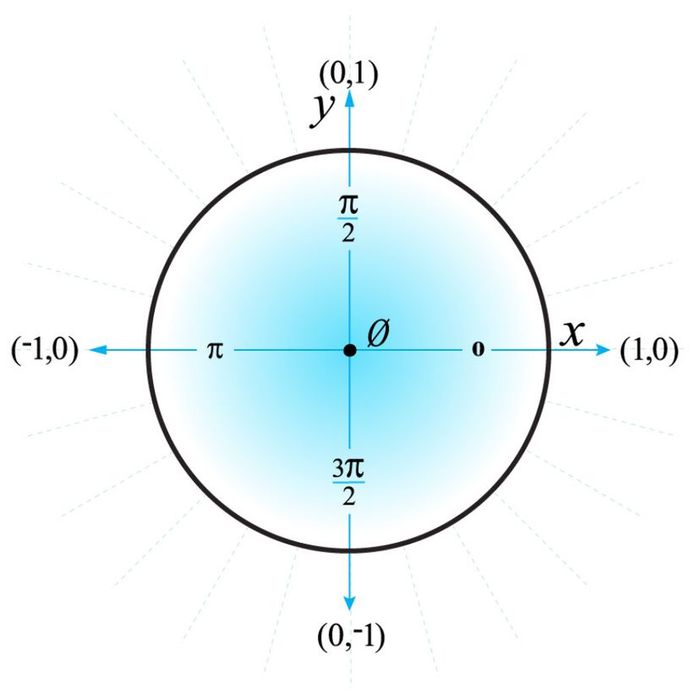Fig. 3. Unit circle displaying four key angles measured in radians
© Mytour 2021Step 2: 3 Pies for $6
Begin with "3 pies." Observe the y-axis: the radian angles adjacent to it, both right and left, share a denominator of 3. All other angles feature a numerator that includes the mathematical constant pi, denoted as π.
The phrase "3 pies for 6" helps remember the remaining 12 angles in a standard unit circle, with three angles per quadrant. Each angle is expressed as a fraction.
The phrase "for $6" serves as a reminder that, within each quadrant, the remaining denominators are 4 followed by 6.
The most challenging aspect of this step is determining the numerator for each fraction.
In the second quadrant (the top-left quarter of the circle), place 2, 3, and 5 before π in the numerators.
Fig. 4. Unit circle with all denominators filled in and some numerators completed (specifically in quadrant 2).
© Mytour 2021The initial angle in quadrant 2 is 2π/3. This is derived by adding the numerator 2 and the denominator 3, resulting in 5.
Observe the angle directly opposite in quadrant 4 (the bottom-right quarter of the circle). Place this 5 in the numerator before π. Repeat this method for the remaining two angles in quadrants 2 and 4.
We’ll apply the same approach to quadrants 1 (top right) and 3 (bottom left). Keep in mind that just as x is equivalent to 1x, π is the same as 1π. Therefore, we add 1 to all denominators in quadrant 1.
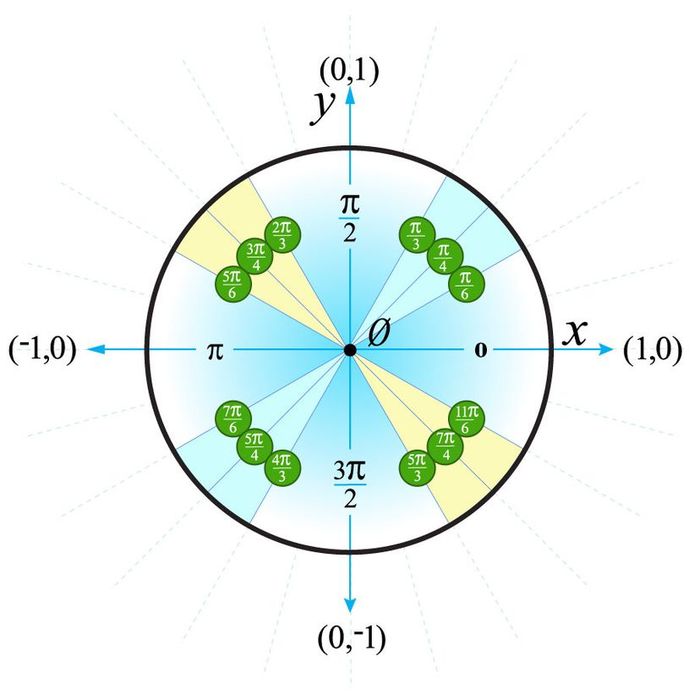Fig. 5. Unit circle with all denominators and numerators fully completed
© Mytour 2021The method for listing angles in degrees, rather than radians, is explained at the conclusion of this article.
Step 3: 2 Square Tables
The number "2" in "2 square tables" serves as a reminder that all 12 remaining coordinate pairs share a denominator of 2.
The term "square" indicates that the numerator of each coordinate includes a square root. For simplicity, we begin with quadrant 1. (Tip: Since the square root of 1 is 1, these fractions can be reduced to 1/2.)
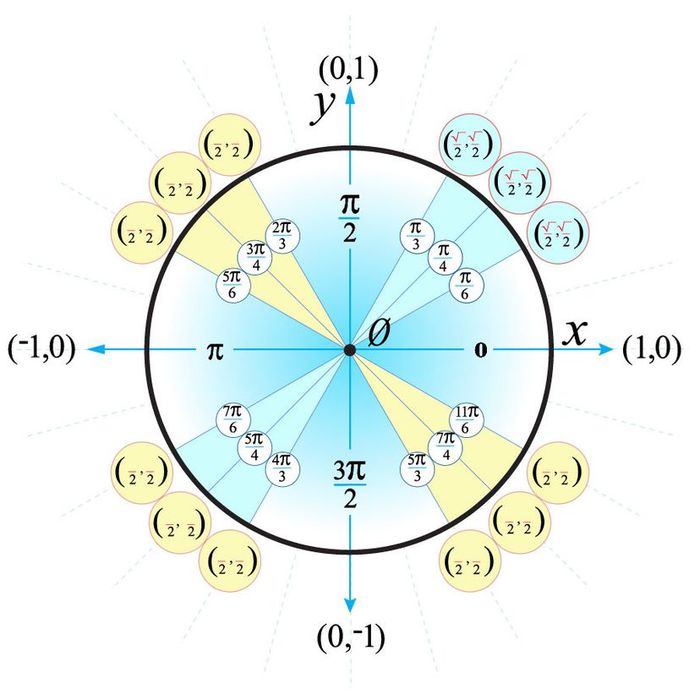Fig. 6. Quadrant 1 fully completed.
© Mytour 2021Step 4: 1, 2, 3
The sequence "1, 2, 3" indicates the numbers under each square root. For the x-coordinates in quadrant 1, we count from 1 to 3, starting at the top coordinate and moving downward.
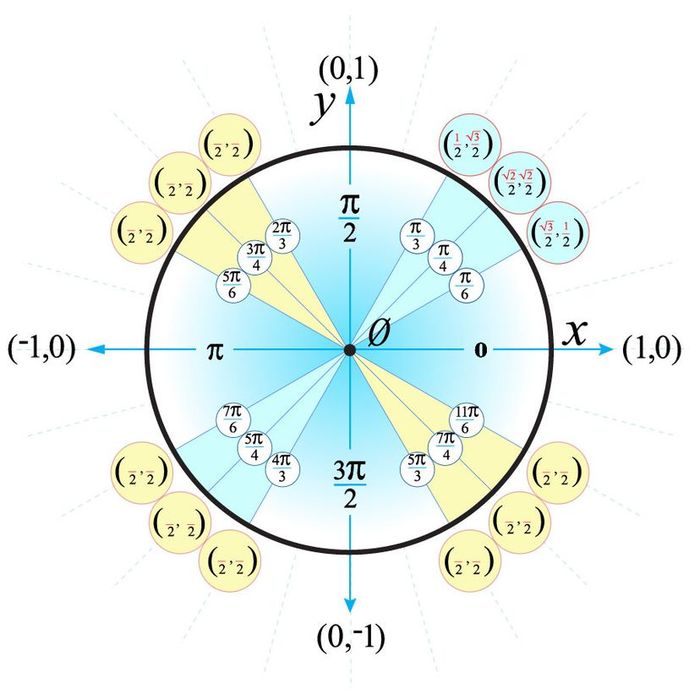Fig. 7. Quadrant 1 of the unit circle with all coordinates filled in.
© Mytour 2021The y-coordinates share the same numerators but are counted from 1 to 3 in reverse order, starting from the bottom and moving upward.
Quadrant 2 mirrors quadrant 1 in coordinates, but the x-coordinates are negative.
In quadrant 3, the x- and y-coordinates from quadrant 1 are swapped, and both coordinates are negative.
Similar to quadrant 3, quadrant 4 also swaps the x- and y-coordinates from quadrant 1, but only the y-coordinates are negative.
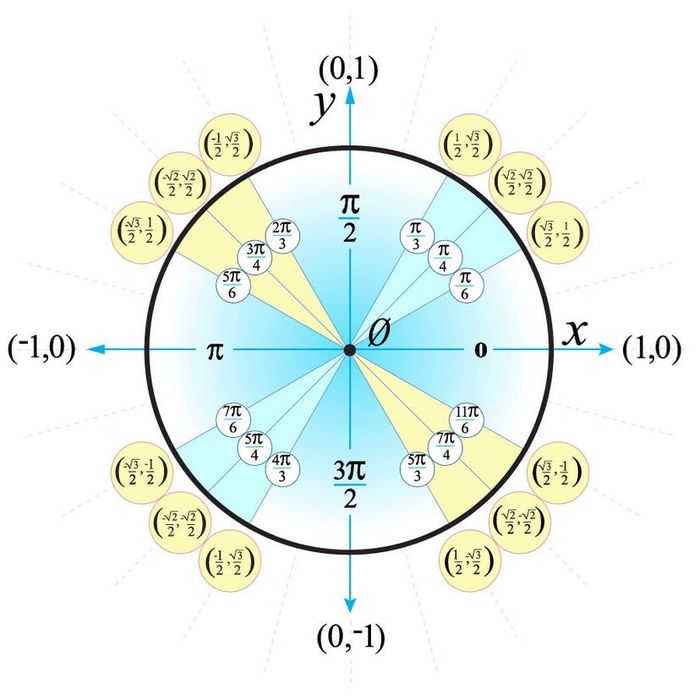Fig. 8. Unit circle with all quadrant coordinates fully completed.
© Mytour 2021Angles in Degrees
If you prefer referencing angles in degrees rather than radians, begin at 0 degrees at the coordinate (1,0). From there, increment by 30, 15, 15, and then 30. In quadrant 1, add 30 to 0 to reach 30, then 15 to 30 for 45, 15 to 45 for 60, and finally 30 to 60 to achieve 90.
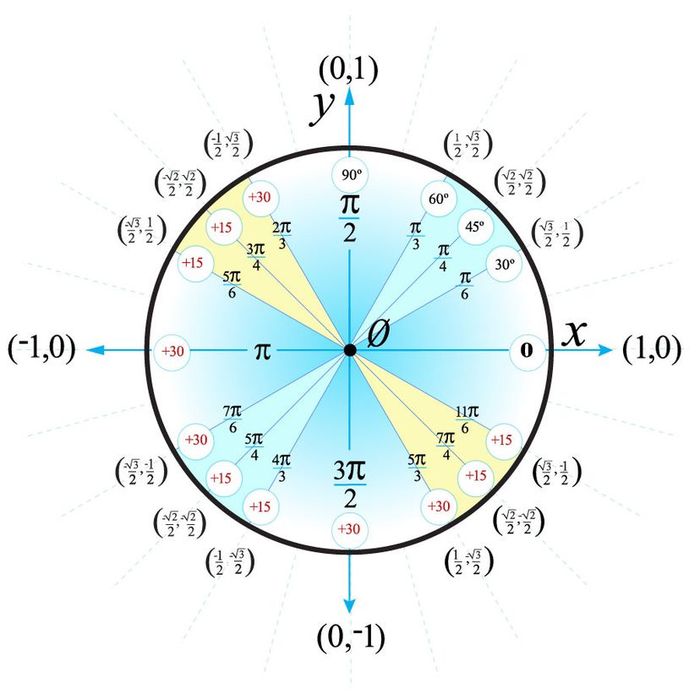Fig. 9. Unit circle displaying angles in degrees for quadrant 1.
© Mytour 2021We follow the same pattern for the remaining quadrants, adding 30, 15, 15, and 30 degrees sequentially until we complete the circle. Quadrant 4, for instance, will cover angles from 270 to 330 degrees (as shown in figure 10).
Using the Unit Circle in Practice
Recall that the unit circle can help determine the two unknown sides of a right triangle with a 30-degree angle and a hypotenuse of 7 units. Let’s apply this concept.
Identify the position of 30° on the unit circle. Use this angle and the x-axis to form a triangle as described.
Fig. 10. Applying the unit circle to determine the two unknown sides of a right triangle with a 30-degree angle.
© Mytour 2021
Fig. 11
© Mytour 2021In a unit circle, any line extending from the center to the edge has a length of 1. Thus, the hypotenuse of this triangle will measure 1 unit. The hypotenuse, being the longest side of a right triangle, intersects the circle's perimeter at the coordinates (√3/2, 1/2).
From this, we deduce that the base of the triangle (along the x-axis) is √3/2 units long, and the height of the triangle is 1/2 units.
An alternative perspective is that the base measures √3/2 times the hypotenuse's length, while the height is 1/2 times the hypotenuse's length.
Therefore, if the hypotenuse measures 7 units, the base of the triangle will be 7 multiplied by √3/2, resulting in 7√3/2.
The height of the triangle will be 7 multiplied by 1/2, equaling 7/2.
Trigonometry is believed to have originated in the 1st century B.C.E. for the study of astronomy, focusing on stars and the solar system. Today, it remains essential for space exploration, utilized by organizations like NASA and private spaceflight companies.
