Understanding the Velocity Formula

Key Takeaways

While we don’t intend to criticize speeding tickets as a means of ensuring public safety (and a source of municipal revenue), perhaps law enforcement should consider rebranding them as "velocity tickets."

Let us explain. Although related, the terms "speed" and "velocity" are not interchangeable in the realm of physics; they refer to distinct concepts.

Velocity, Defined

Speed measures the total distance an object covers within a specific time frame.

Velocity, however, introduces an additional element. As a "vector quantity," velocity accounts for both magnitude and direction. In contrast, speed is a "scalar quantity," focusing solely on magnitude without considering direction.

Michael Richmond, Ph.D., a professor at Rochester Institute of Technology's School of Physics and Astronomy, describes velocity as "the rate at which displacement changes over time."

Covering Ground

So, what exactly is "displacement?" Simply put, it refers to an object's change in position, or the difference between its starting point and final location.

It’s important to note that an object’s change in position doesn’t always match the total distance it has traveled. This might seem confusing at first, but stay with us.

If you run one lap around a perfect 8-foot (2.4-meter) circle, the distance you’ve covered will be exactly 8 feet.

However, you’ll end up right back where you started. This means your displacement will be 0 feet (or 0 meters), despite having covered a certain distance.

Learning By Example

Let’s consider another scenario.

Imagine you’re at the gym chatting with someone. If they mention, "Gary ran 39.3 feet (12 meters) in three seconds today," they’re providing his speed, not his velocity.

To determine Gary’s velocity, additional details would be necessary.

If our gym companion mentioned, "Gary ran 39.3 feet (12 meters) west in three seconds today," we’d have a clear idea of his direction, giving us a solid starting point.

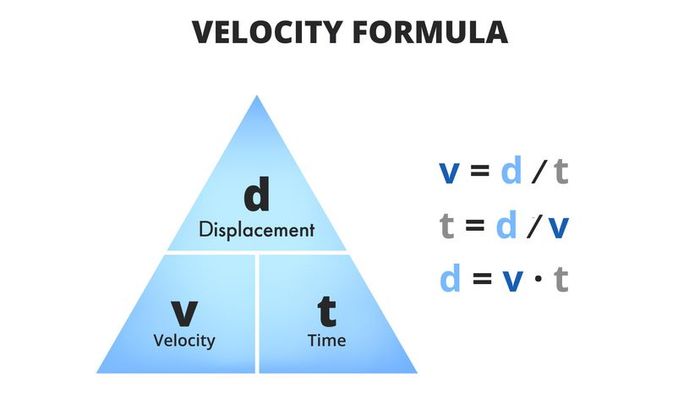
The equation to determine an object’s velocity is as follows:

In this formula, "v," "d," and "t" stand for "velocity," "displacement," and "time," respectively. In simpler terms, velocity equals displacement divided by time.

When applying this formula, ensure you measure displacement in meters and time in seconds. For clarity, let’s assume Gary ran westward in a perfectly straight 12-meter (32.8-foot) line, meaning his displacement matches the distance he covered.

We also know that Gary took three seconds to move from his starting point to his final position.

So, when we input the values, the calculation looks like this:

Thus, Gary’s average velocity while moving westward was 4 meters per second (13.12 feet per second).

(Note the importance of phrasing here. We’ve only calculated Gary’s average velocity; the concept of instantaneous velocity, which modifies the formula discussed earlier, remains a separate topic.)

Velocity Formula Calculator

Closing Comments

Now, about those so-called "speeding" tickets. If you’ve ever been issued one, the direction your vehicle was moving must have played a role. Whether consciously or not, it’s something both you and the officer likely considered.

What’s worse than driving excessively fast? Driving excessively fast in the wrong direction. (Think one-way streets or even two-lane roads where one side is required to drive slower.)

So, based on everything we’ve discussed, it’s fair to argue that "speeding tickets" might be more accurately named "velocity tickets" or something along those lines. Good night, everyone.