What exactly is a Perfect Square?

You already know what a square is: a shape with four equal sides. Seems simple, right? But what makes a square perfect? To understand this, we’ll need to explore some mathematics.

Understanding Perfect Squares

A perfect square is a unique kind of number that you obtain by multiplying a number by itself. It's similar to a square shape — symmetrical, orderly, and fascinating.

For example, when you multiply 5 by 5, the result is 25, which makes 25 a perfect square since it's the product of 5 x 5.

Recognizing Perfect Squares

So, how do you figure out if a number is a perfect square? The key is to find its square root, which is the inverse of squaring a number. If the square root is a whole number, you’ve got yourself a perfect square.

For instance, the square root of 16 is 4 because 4 x 4 equals 16, making 16 a perfect square. Similarly, the square root of 144 is 12 because 12 x 12 equals 144. And there you have it — another perfect square.

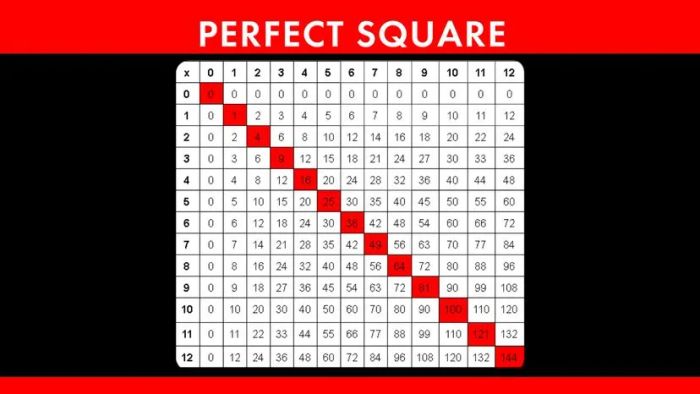
Chart of Perfect Squares

To give you a clearer understanding of perfect squares, here are some additional examples that are commonly seen:

As you can observe, each of these values can be represented as the product of two identical integers, which defines them as perfect squares.

Defining the Characteristics of a Perfect Square

After we have defined perfect squares and how to identify them, let's dive into a few more intriguing details that will enhance our understanding.

When you examine perfect squares, you’ll notice an interesting pattern: The last digit of a perfect square is always one of these: 0, 1, 4, 5, 6, or 9. This can be very useful when quickly spotting perfect squares.

If you want to manually calculate perfect squares, try using the long multiplication method, which can be quite effective.

Perfect squares go beyond just small numbers; they reach much further. Take 625, for example, a perfect square because it’s the product of 25 x 25. Exploring larger perfect squares is an exciting mathematical adventure.

The Beauty of Perfect Squares

Perfect squares are not merely mathematical wonders; they are also practical tools with real-world uses in areas like geometry and algebra. Grasping their significance can deepen your overall understanding and appreciation of mathematics.