Hãy hình dung bạn đang ngồi tại trường quay của chương trình 'Ai là triệu phú', và đây là câu hỏi dành cho bạn.
Đây là một bài toán đơn giản: 1 trừ 1 bằng bao nhiêu?
Câu trả lời dĩ nhiên là 0.
Có lý do nào khiến chúng ta nghi ngờ về đáp án này không? Chắc chắn là không! Trong mọi trường hợp, 1 trừ 1 đều phải bằng 0.
Nhưng nếu chúng ta cộng thêm 1, kết quả 1-1+1 sẽ là 1. Sau đó lại trừ đi 1, phép tính 1-1+1-1 lại trở về 0. Mọi thứ vẫn ổn. Nhưng nếu tiếp tục lặp lại phép tính này đến vô tận thì sao?
1 – 1 + 1 – 1 + 1 – 1 + ...
Kết quả cuối cùng của phép tính này là bao nhiêu?
Câu hỏi nghe có vẻ đơn giản, thậm chí có người cho rằng đây là một phép toán vô nghĩa. Nhưng đừng coi thường sự phức tạp của toán học. Chính phép toán này đã khiến bao thế hệ nhà toán học, triết gia và thậm chí cả những nhà tu hành đau đầu.
Nếu bạn suy nghĩ về đáp án này đến mức tận cùng, nó có thể khiến bạn hoài nghi về bản chất của cuộc sống, chẳng hạn: 'Liệu có một Đấng Tạo Hóa nào tạo ra vũ trụ không? Liệu các vũ trụ song song có tồn tại không? Và nếu có, kết quả phép tính này ở một vũ trụ khác liệu có khác?
Bạn có tin không? Nếu không, hãy thử suy ngẫm.

Hình minh họa
Hãy tưởng tượng bạn đang trong trường quay của 'Ai là triệu phú'. Người dẫn chương trình đặt câu hỏi: 1-1+1-1+1-... bằng bao nhiêu? Và dưới đây là 4 lựa chọn:
A. 0
B. 1
C. ½
D. Không có giá trị cụ thể.
Nếu bạn chọn đáp án A. 0, có thể bạn đã áp dụng cách đơn giản là nhóm các số hạng của phép toán lại: (1 – 1) + (1 – 1) + (1 – 1) + ...
Hãy nhớ rằng theo quy tắc toán học, chúng ta cần thực hiện các phép toán trong dấu ngoặc trước. Do đó, mỗi phép trừ trong ngoặc (1 – 1) đều cho kết quả là 0. Cuối cùng, toàn bộ phép toán trở thành 0 + 0 + 0 + ..., rõ ràng là bằng 0.
Tuy nhiên, thử thay đổi một chút về cách đặt dấu ngoặc. Thay vì nhóm hai số đầu tiên, hãy nhóm số thứ hai và thứ ba, và tiếp tục như vậy. Phép tính sẽ trở thành: 1 + (–1 + 1) + (–1 + 1) + (–1 + 1) + ...
Một lần nữa, các phần trong ngoặc cộng lại đều bằng 0, nhưng chúng ta vẫn còn số 1 ở đầu. Kết quả cuối cùng là 1. Vì vậy, đáp án B cũng có thể đúng.

Hình minh họa.
Có thể bạn đang tự hỏi ai là người nghĩ ra bài toán kỳ quặc này?
Tài liệu toán học cho biết chuỗi số vô hạn này được nhà toán học và tu hành người Ý Luigi Guido Grandi đưa ra vào năm 1703. Chuỗi này sau đó được đặt tên là chuỗi Grandi.
Grandi là người phát hiện ra chuỗi số này và nhận thấy rằng bằng cách thay đổi vị trí dấu ngoặc, ông có thể khiến tổng của chuỗi này bằng 0 hoặc 1.
Theo nhà sử học toán học Giorgio Bagni, sự mâu thuẫn trong phép tính này mang ý nghĩa thần học đối với Grandi, người tin rằng nó chứng minh việc tạo ra điều gì đó từ hư vô là 'hoàn toàn hợp lý'. Grandi dựa vào điều này để duy trì niềm tin vào một Đấng Tạo Hóa đã tạo ra thế giới.
Việc chuỗi số Grandi có thể có tổng là 0 hay 1 rõ ràng là một sự mâu thuẫn. Nhưng chắc chắn nó không mâu thuẫn bằng đáp án C. ½.
Làm thế nào mà tổng của một chuỗi số vô hạn lại có thể là một phân số? Nghe có vẻ vô lý, nhưng cuối cùng, Grandi và nhiều nhà toán học nổi tiếng thế kỷ 18 đã kết luận rằng tổng của chuỗi này thực sự bằng một nửa.
Grandi đã sử dụng một câu chuyện ngụ ngôn để giải thích cho lập luận của mình:
Hãy hình dung hai anh em trong một gia đình thừa kế một viên ngọc quý từ cha. Mỗi người sẽ giữ viên ngọc trong một năm và sau đó chuyển nó cho người kia. Nếu quá trình trao đổi này được tiếp tục qua nhiều thế hệ, cả hai gia đình chỉ có 1/2 quyền sở hữu viên ngọc.

Luigi Guido Grandi, nhà toán học và là người khai sinh ra chuỗi số mang tên ông.
Câu chuyện trên có thể chưa đủ thuyết phục bạn, nhưng Gottfried Wilhelm Leibniz, một nhà triết học và toán học người Đức, đã đưa ra một lập luận khác: nếu bạn cộng dãy số này và dừng ở một điểm bất kỳ, tổng nhận được sẽ bằng 0 hoặc 1.
Xác suất của cả hai kết quả là như nhau. Vì vậy, theo nguyên lý toán xác suất, bạn phải lấy trung bình tất cả kết quả để tìm ra đáp án cuối cùng. Tổng chuỗi Grandi do đó sẽ bằng ½.
Dù Leibniz tin rằng kết quả của mình đúng, ông vẫn thừa nhận rằng lập luận của mình 'thiên về siêu hình học hơn là toán học'. Hơn nửa thế kỷ sau, nhà toán học Leonhard Euler đã xuất bản một nghiên cứu chặt chẽ để chứng minh rằng chuỗi 1 – 1 + 1 – 1 + ... có tổng bằng một nửa.
Năm 1760, Euler đã công bố bài nghiên cứu dài 33 trang với tựa đề 'De Seriebus divergentibus' (tạm dịch là Về chuỗi phân kỳ), trong đó ông khẳng định 'không còn nghi ngờ gì nữa, chuỗi số 1 – 1 + 1 – 1 + ... và phân số 1/2 là tương đương'.
Trở lại câu hỏi trong chương trình Ai là triệu phú, nếu bạn tham khảo ý kiến khán giả, hầu hết sẽ chọn đáp án C. 1/2.

Hầu hết mọi người thông minh đều nghiêng về đáp án C.
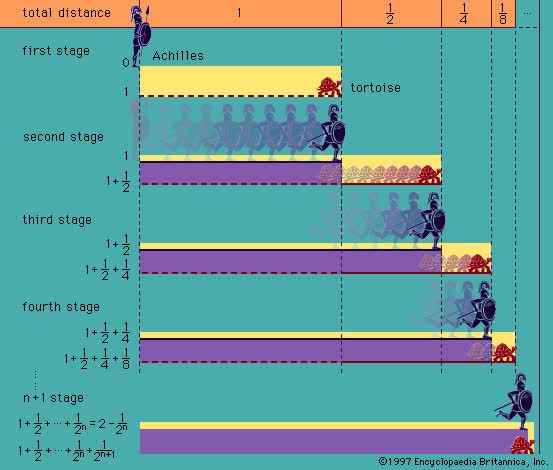
Khó khăn trong việc hiểu các chuỗi số vô hạn đã làm đau đầu các nhà toán học từ thời Hy Lạp cổ đại. Bạn còn nhớ Nghịch lý Achilles và con rùa không?
Achilles, anh hùng trong thần thoại Hy Lạp và người nổi tiếng với tốc độ nhanh như gió, đang đuổi theo một con rùa. Nếu Achilles chấp con rùa một khoảng cách a mét và a không bằng 0, đồng thời cả hai có tốc độ không đổi.
Để thắng con rùa, Achilles cần phải bắt kịp nó trước. Tuy nhiên, mỗi lần anh rút ngắn khoảng cách xuống một nửa, con rùa lại di chuyển thêm một đoạn nhỏ nữa.
Achilles phải tiếp tục chạy thêm một nửa khoảng cách còn lại để cố gắng bắt kịp, nhưng trong thời gian đó, con rùa lại tiếp tục di chuyển thêm một quãng đường nhỏ. Quá trình này lặp đi lặp lại, khiến Achilles không bao giờ có thể bắt kịp hay vượt qua con rùa.
Nghịch lý Zeno.
Triết gia Hy Lạp Zeno của xứ Elea đã kể một câu chuyện vào năm 400 trước Công Nguyên, nêu bật một nghịch lý nổi tiếng trong toán vi tích phân. Nghịch lý này giúp giải thích khi nào tổng của một chuỗi số vô hạn có thể đạt được một giá trị hữu hạn.
Chúng ta sẽ tìm hiểu khái niệm tổng riêng thứ n của một chuỗi số. Giả sử bạn có một chuỗi số vô hạn, tổng riêng thứ n (Sn) là tổng của n số hạng đầu tiên trong chuỗi. Ví dụ, S2 là tổng của hai số đầu tiên, S3 là tổng của ba số đầu tiên, S5 là tổng của năm số đầu tiên, và cứ thế tiếp tục.
Nếu các tổng trung gian này ngày càng tiến gần đến một giá trị cố định, chúng ta nói rằng chuỗi số 'hội tụ' về giá trị đó. Áp dụng điều này vào chuỗi trong Nghịch lý Zeno, tổng của nửa con đường, cộng thêm một phần tư, phần tám, và cứ thế:
½ + ¼ + ⅛ + 1/16 + …
Tổng của hai số đầu tiên là S2= 0.75, tổng của ba số đầu tiên là S3= 0.875, và tổng của bốn số đầu tiên là S4= 0.9375. Nếu cộng 10 số đầu tiên, ta có S10= 0.9990234375.
Các tổng riêng thứ n tiếp tục như vậy và ngày càng gần giá trị 1. Vì vậy, ta có thể kết luận rằng chuỗi số hội tụ về 1. Dù chúng ta có thể tưởng tượng một con đường là vô hạn, vi tích phân chứng minh rằng nó vẫn kết thúc ở một điểm cụ thể.
Giờ đây, quay lại chuỗi số Grandi, tổng riêng thứ n của chuỗi 1-1+1-1+1-…, Sn, sẽ dao động giữa 0 và 1 mà không bao giờ ổn định về một giá trị cụ thể. Vì vậy, các nhà toán học hiện đại thường chọn phương án D. Không bao nhiêu cả.

Ảnh minh họa.
Việc giải quyết chuỗi số Grandi đặt ra một vấn đề mang tính xã hội học: Tại sao cộng đồng toán học lại chấp nhận cách giải của tổng riêng thứ n mà không chấp nhận lập luận xác suất của Leibniz hay các định nghĩa khác về cộng chuỗi số vô hạn?
Một phần lý do là việc cộng một chuỗi số vô hạn không thực sự là phép cộng theo cách chúng ta hiểu. Dù trông có vẻ giống nhau, nhưng cách thực hiện lại khác biệt.
Một đặc điểm quan trọng của phép cộng là kết quả không thay đổi khi ta thay đổi vị trí của dấu ngoặc. Ví dụ, 1 + (2 + 3) = (1 + 2) + 3. Tuy nhiên, đối với nhiều chuỗi số, kể cả chuỗi Grandi, việc di chuyển dấu ngoặc lại có thể làm thay đổi kết quả.
Thực tế, các nhà toán học chỉ mượn khái niệm 'cộng' và 'bằng' từ phép cộng để làm cho việc thảo luận về chuỗi số trở nên dễ dàng hơn. Về bản chất, một chuỗi số không thể 'cộng' theo cách thông thường, mà chỉ có thể 'hội tụ' về một giá trị.
Khi chúng ta nói rằng một chuỗi số hội tụ về một giá trị thay vì có tổng cụ thể, điều này giúp giải quyết nhiều mâu thuẫn của các chuỗi số vô hạn mà các nhà toán học trước đây không thể giải quyết được trong hàng thế kỷ.
Nhưng đối với các chuỗi số không hội tụ như chuỗi Grandi thì sao?
Các nhà toán học vẫn có cách tính tổng của chuỗi số, hay nói cách khác, xác định giá trị hội tụ của nó. Phương pháp này được gọi là tổng Cesàro, đặt theo tên nhà toán học Ý Ernesto Cesàro, người phát minh ra nó vào thế kỷ 19.
Cesàro giải thích rằng, ngay cả khi một chuỗi số vô hạn không hội tụ theo cách thông thường, tức là không tiến gần đến một giá trị cụ thể khi số hạng ngày càng nhiều, ta vẫn có thể tính tổng của nó bằng cách lấy trung bình của các tổng riêng thứ n của chuỗi.
Ví dụ, thay vì chỉ xét Sn, phương pháp tổng Cesàro lấy trung bình của S1 và S2, sau đó là S1, S2 và S3, rồi S1, S2, S3, S4, và cứ tiếp tục như vậy để xem các tổng riêng này hội tụ về đâu.
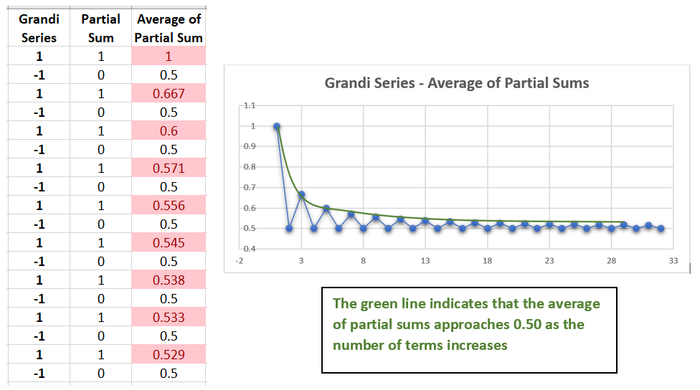
Tổng Cesàro của chuỗi số Grandi là 1/2.
Điều thú vị là nếu bạn áp dụng phương pháp này cho một chuỗi số hội tụ như chuỗi của Zeno, bạn sẽ luôn nhận được kết quả tương tự. Tuy nhiên, phương pháp này đôi khi cho kết quả khác với chuỗi số không hội tụ theo định nghĩa chuẩn. Cụ thể, tổng Cesàro của chuỗi Grandi là 1/2.
Ngày càng có nhiều phương pháp tính tổng cho các chuỗi số được phát triển. Mặc dù các phương pháp này có thể cho kết quả khác nhau trên cùng một chuỗi, nhưng không tạo ra mâu thuẫn nếu các định nghĩa được quy ước trước.
Điều kỳ lạ là hầu hết các phương pháp tính tổng của chuỗi Grandi đều cho kết quả là ½.
Vậy, nếu phải đưa ra một câu trả lời đơn giản cho câu hỏi trong chương trình 'Ai là triệu phú', chuỗi 1-1+1-1+1-… thì bằng bao nhiêu? Câu trả lời cuối cùng là: Chuỗi Grandi không có tổng cụ thể nào, nhưng nếu phải xác định thì tổng đó gần nhất là ½.
Toán học chỉ có thể giúp bạn đến một mức độ nhất định. Quay trở lại trường quay của chương trình Ai là triệu phú, nếu bạn vẫn còn sự trợ giúp 50/50, hãy tận dụng nó xem sao.
