1. Khám phá lý thuyết về 7 hằng đẳng thức cơ bản
Đối với hai biểu thức A và B, chúng ta có thể xác lập 7 hằng đẳng thức như sau:
- Bình phương của tổng bằng bình phương của số đầu tiên cộng hai lần tích của số đầu tiên với số thứ hai, cộng thêm bình phương của số thứ hai.
(A + B)² = A² + 2AB + B²
- Bình phương của một hiệu là bình phương của số đầu trừ đi hai lần tích của số đó với số còn lại, sau đó cộng với bình phương số còn lại:
(A - B)² = A² - 2AB + B²
⇒ A² + B² = (A - B)² + 2AB = (A + B)² - 2AB
- Hiệu của hai bình phương bằng hiệu của hai số nhân tổng của chúng
(A + B)(A - B) = A² - B²
- Lập phương của một tổng bằng lập phương của số đầu cộng với ba lần tích của bình phương số đầu và số còn lại, cộng thêm ba lần tích của số đầu và bình phương số còn lại, và cuối cùng là lập phương của số còn lại:
(A + B)³ = A³ + 3A²B + 3AB² + B³
(A - B)³ = A³ - 3A²B + 3AB² - B³
- Lập phương của một tổng được tính bằng lập phương số đầu cộng với ba lần tích của bình phương số đầu và số còn lại, thêm ba lần tích số đầu với bình phương số còn lại, và cuối cùng là lập phương số còn lại
(A + B)(A² - AB + B²) = A³ + B³
- Lập phương của một hiệu bằng lập phương của số đầu trừ đi ba lần tích bình phương số đầu với số còn lại, cộng thêm ba lần tích số đầu với bình phương số còn lại, và cuối cùng trừ đi lập phương của số còn lại.
Diễn giải bằng lời: Lập phương của một tổng bằng lập phương của số đầu trừ đi ba lần tích của bình phương số đầu và số còn lại, cộng với ba lần tích số đầu với bình phương số còn lại, và trừ đi lập phương của số còn lại.
- Hiệu của hai lập phương bằng hiệu của hai số đó nhân với bình phương tổng của hai số.
(A - B)(A² + AB + B²) = A³ - B³
2. Bài tập ứng dụng
Bài tập 1: Áp dụng 7 hằng đẳng thức để viết các biểu thức sau dưới dạng tổng.
a. (2x + 1)² = 4x² - 4x + 1
b. (2x + 3y)² = 4x² + 2 × 2x × 3y + 9y² = 4x² + 12xy + 9y²
c. (x + 1)(x - 1) = x² - 1
d. m² - n² = (m - n) × (m + n)
Bài tập 2: Áp dụng 7 hằng đẳng thức để rút gọn biểu thức sau:
A = (x + y)² - (x - y)²
A = (x + y)² - (x - y)² = x² + 2xy + y² - (x² - 2xy + y²) = 4xy
3. Các dạng biến đổi cần chú ý
- Lưu ý khi thực hiện các phép toán, bao gồm nhân đơn thức với đa thức, nhân đa thức với đa thức, và áp dụng hằng đẳng thức. Các bài toán yêu cầu viết lại biểu thức cần chú ý đến quy tắc nhân đa thức và ghi nhớ 7 hằng đẳng thức quan trọng. Đặc biệt lưu ý dấu của các số hạng và dấu các phép toán.
- Áp dụng các đặc điểm của 7 hằng đẳng thức quan trọng để giải quyết vấn đề.
Bài tập tìm giá trị nhỏ nhất của biểu thức. Bước đầu tiên là biến đổi biểu thức về dạng M = A² + B, với A là biểu thức chứa biến và B là một số hoặc một biểu thức số độc lập. Vì bình phương của mọi số thực luôn không âm, nên A² ≥ 0 với mọi giá trị của biến, do đó A² + B ≥ B. Giá trị nhỏ nhất của biểu thức là B, xảy ra khi A = 0.
Dạng 1: Thực hiện phép toán cụ thể:
Phương pháp giải: Áp dụng trực tiếp các hằng đẳng thức đã học để khai triển biểu thức.
Dạng 2: Chứng minh các đẳng thức:
Phương pháp giải: Sử dụng linh hoạt các hằng đẳng thức và lựa chọn các vế phù hợp để dễ dàng áp dụng các hằng đẳng thức.
Dạng 3: Tính toán nhanh
Phương pháp giải: Áp dụng linh hoạt các hằng đẳng thức vào các bài toán với số tự nhiên.
Dạng 4: Xác định giá trị lớn nhất và nhỏ nhất của biểu thức
Phương pháp giải: Áp dụng các hằng đẳng thức và lưu ý những điểm sau:

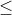
Dạng 4: Áp dụng hằng đẳng thức để khai triển, rút gọn và tính giá trị của biểu thức.
Phương pháp giải: Sử dụng các hằng đẳng thức đã học để mở rộng và đơn giản hóa biểu thức.
Phương pháp 5: Áp dụng hằng đẳng thức để tính toán nhanh chóng
Cách giải: Linh hoạt áp dụng các hằng đẳng thức đã học để tính toán nhanh
Phương pháp 6: Áp dụng hằng đẳng thức để khai triển hoặc đơn giản hóa biểu thức
Cách giải: Sử dụng hằng đẳng thức để mở rộng hoặc đơn giản hóa biểu thức
Phương pháp 7: Áp dụng hằng đẳng thức để tính toán nhanh chóng
Cách giải: Áp dụng các hằng đẳng thức đã học để phân tích và thực hiện tính toán
4. Bài tập để tự luyện tập
Câu 1. Xây dựng biểu thức tính diện tích của hình vuông với cạnh là 2x + 3 dưới dạng đa thức
b. Xây dựng biểu thức tính thể tích của khối lập phương với cạnh là 3x - 2 dưới dạng đa thức
Câu 2: Thực hiện tính nhanh các bài sau:
a. 38 nhân 42
b. 102 chia 2
c. 198 chia 2
d. 75 chia 2 trừ 25 chia 2
Câu 3: Chuyển các biểu thức sau thành dạng đa thức
a. (2x - 3) lũy thừa 3
b. (a + 3b) lũy thừa 3
c. (xy - 1) lũy thừa 3
Câu 4: Chứng minh rằng biểu thức (4n + 3) lũy thừa 2 - 25 chia hết cho 8 với mọi số nguyên n
Câu 5: So sánh hai biểu thức sau, biểu thức nào lớn hơn?
a. A = (2 + 1) (2 x 2 + 1) (2 x 4 + 1) và B = 2 x 2
Câu 6: Tìm ba số tự nhiên liên tiếp sao cho tổng của các tích của từng cặp số trong ba số đó là 74.
Câu 7: Hiệu của các bình phương của hai số tự nhiên lẻ liên tiếp là 40. Tìm hai số đó.
Câu 8: Tổng của ba số a, b, c bằng 9. Tổng các bình phương của chúng là 53. Tính giá trị của ab + bc + ca.
Câu 9: Xác định giá trị của các biểu thức sau:
a. x² - 10x + 26 khi x = 105
b. x² + 0,2x + 0,01 khi x = 0,9
Câu 10: Xác định giá trị nhỏ nhất của các biểu thức sau:
a. A = x² - 4x + 1
b. B = 4x² + 4x + 11
c. C = 3x² - 6x - 1
Câu 11: Tính toán các biểu thức sau cho chính xác
a. (x + 2y) lũy thừa 2
b. (2x + 3y) lũy thừa 2
c. (3x - 2y) lũy thừa 2
d. (5x - y) lũy thừa 2
e. (x + 1/4) lũy thừa 2
f. (1/3 x - 1/2) lũy thừa 2
g. (x + 1) lũy thừa 2
(3x + 1) (3x - 1)
h. (x² + 2/5 y) (x² - 2/5 y)
i. x² - 6x + 9
k. 1/4 x² + 2xy² + 4y²
m. x³ - 8y³
n. a⁶ - b³
l. x² - 10x + 25
o. x² + 4xy + 4y²
Câu 12: Thực hiện tính toán nhanh
a. 10001 lũy thừa 2
b. 29,9 nhân 40,1
c. 201 lũy thừa 2
d. 199 lũy thừa 2
e. 20,1 nhân 19,9
f. 33,3 lũy thừa 2 - 2 x 33,33 + 3,3 lũy thừa 2
Câu 13: Điền vào chỗ trống: .... = (2x - 1) (4x² + 2x + 1)
Câu 14: Tính giá trị của biểu thức A = 8x³ + 12x²y + 6xy² + y³ khi x = 2 và y = -1
Câu 15: Tính giá trị của biểu thức A = 352 - 700 + 10²
Câu 16: Tìm giá trị của x sao cho biểu thức sau đúng:
2x² - 4x + 2 = 0, x có giá trị là bao nhiêu?
Câu 17: Có bao nhiêu giá trị của x để thỏa mãn (2x + 1)² - 4(x + 3)²?
Câu 18: Đơn giản hóa biểu thức sau:
N = (2x + 3y) (4x² - 6xy + 9y²)
P = (x - y) (x² + xy + y²) - (x + y) (x² - xy + y²)
Q = (x² - 2y) (x⁴ + 2x²y + 4y²)
Bài viết trên Mytour đã cung cấp thông tin chi tiết về 7 hằng đẳng thức quan trọng và bài tập ứng dụng. Nội dung và đáp án đã được đề cập. Cảm ơn bạn đã theo dõi.
