1. Các dạng bài toán liên quan đến hình học
Dạng 1: Các bài toán về hình học phẳng
Các phương pháp giải bài toán hình học phẳng được phân chia thành 3 dạng cơ bản
Dạng 1: Bài toán không liên quan đến thực tế: Đề bài cung cấp hình vẽ và số liệu, yêu cầu tính toán diện tích, chu vi hoặc một cạnh của hình
Dạng 2: Bài toán có nội dung thực tế: Đề bài chứa dữ liệu liên quan đến tình huống đời sống hàng ngày
Dạng 3: Đối với loại bài toán này, cần nhớ và áp dụng công thức tính chu vi và diện tích của các hình học phẳng như hình vuông, chữ nhật, tam giác, tròn, thang, và bình hành
Ví dụ: Một thửa đất hình thang có đáy lớn dài 120 m, đáy nhỏ bằng 2/3 đáy lớn và dài hơn chiều cao 5 m. Trung bình, mỗi 100 m² thu hoạch được 72 kg thóc. Tính tổng số kg thóc thu hoạch được trên thửa đất đó.
Đáp án: Đáy nhỏ dài là 120 x 2/3 = 80 m
Chiều cao được tính là 80 - 5 = 75 m
Diện tích của thửa ruộng được tính theo công thức 120 + 80 x 75 / 2 = 7.500 mét vuông
Số kg thóc thu hoạch được là 7.500 chia 100 x 72 = 5.400 kg
Dạng 2: Các bài toán về hình khối
Phương pháp giải: Các bài toán thường liên quan đến hình lập phương và hình hộp chữ nhật. Để giải, cần nắm vững cách tính diện tích xung quanh, diện tích toàn phần và thể tích của các hình khối này.
Ví dụ: Một thùng hàng có nắp hình hộp chữ nhật với chiều dài 2,5 m, chiều rộng 1,8 m và chiều cao 2 m. Cần bao nhiêu kg sơn để phủ mặt ngoài của thùng? Biết mỗi kg sơn phủ được 5 m².
Đáp án: Diện tích xung quanh của thùng hàng là 2 x (2,5 + 1,8) x 2 = 17,2 mét vuông
Diện tích của hai đáy thùng là 2,5 x 1,8 x 2 = 9 m²
Tổng diện tích mặt ngoài của thùng là 17,2 + 9 = 26,2 mét vuông
Số kg sơn cần dùng là 26,2 / 5 = 5,24 kg
2. Đáp án bài tập Toán lớp 5 bài 119
Bài 1: Cho hình vuông ABCD có cạnh dài 4 cm. Trên các cạnh của hình vuông, ta lần lượt lấy các trung điểm M, N, P, Q. Nối bốn điểm này lại để tạo thành hình tứ giác MNPQ. Tính tỷ số giữa diện tích của hình tứ giác MNPQ và diện tích của hình vuông ABCD.
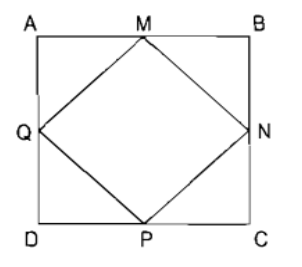
Cách giải:
- Diện tích hình vuông ABCD tính bằng cạnh x cạnh
Các tam giác AMQ, BMN, CPN, DPQ đều là tam giác vuông với diện tích bằng nhau. Diện tích của mỗi tam giác được tính bằng tích của hai cạnh góc vuông chia cho 2.
Diện tích hình tứ giác MNPQ được tính bằng diện tích của hình vuông ABCD trừ đi tổng diện tích của các tam giác AMQ, BMN, CPN, DPQ.
Để tìm tỷ số giữa diện tích hình tứ giác MNPQ và hình vuông ABCD, ta chia diện tích của hình tứ giác MNPQ cho diện tích của hình vuông ABCD.
Đáp án: Vì M, N, P, Q lần lượt là các trung điểm của các cạnh AB, BC, CD, và AD, nên A = MB = PN = NC = CB = PD = PQ = QA = 4:2 = 2 cm.
Diện tích hình vuông ABCD là 4 x 4 = 16 cm².
Diện tích của tam giác AMQ là 2 cm².
Diện tích của hình tứ giác MNPQ được tính là 16 - 4 x 2 = 8 cm².
Tỷ lệ giữa diện tích hình tứ giác MNPQ và diện tích hình vuông ABCD là 8 : 16 = 1/2.
Kết quả là 1/2.
Bài 2: Xét hình chữ nhật ABCD với AD = 2 dm và một nửa hình tròn có tâm O và bán kính 2 dm. Tính diện tích của phần đã được tô đậm trong hình chữ nhật ABCD.
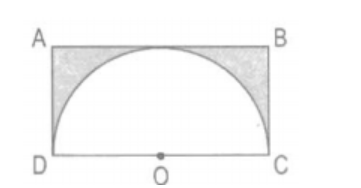
Cách giải:
Để tìm chiều dài của hình chữ nhật, nhân OD với 2.
Diện tích của hình chữ nhật ABCD được tính bằng chiều dài nhân với chiều rộng.
Diện tích của nửa hình tròn với tâm O được tính bằng (bán kính x bán kính x 3,14) chia 2.
Diện tích vùng được tô đậm = Diện tích hình chữ nhật ABCD trừ đi diện tích nửa hình tròn tâm O
Kết quả: Diện tích hình chữ nhật ABCD là 2 x 4 = 8 dm²
Diện tích nửa hình tròn tâm O tính bằng (2 x 2 x 3,14) / 2 = 6,28 dm²
Diện tích vùng tô đậm là 8 - 6,28 = 1,72 dm²
Kết quả cuối cùng: 1,72 dm²
Bài 3: Xem xét hình thang vuông ABCD với các cạnh AB = 20 cm, AD = 30 cm, DC = 40 cm. Khi nối điểm A với điểm C, ta được hai tam giác là ABC và ADC.
a. Tính diện tích của hai tam giác này
b. Tính tỷ lệ phần trăm giữa diện tích của tam giác ABC và tam giác ADC
Phương pháp giải:
- Diện tích hình thang ABCD được tính bằng tổng hai đáy nhân chiều cao chia cho 2, tức là (AB + DC) x AD / 2
Diện tích tam giác ABC được tính bằng AD x DC / 2
Diện tích của tam giác ABC bằng diện tích hình thang ABCD trừ đi diện tích của tam giác ADC
Để tính tỷ lệ phần trăm của diện tích tam giác ABC so với diện tích tam giác ADC, ta lấy diện tích tam giác ABC chia cho diện tích tam giác ADC, rồi nhân kết quả với 100 và gắn ký hiệu phần trăm.
Đáp án:
a. Diện tích hình thang ABCD là (20 + 40) x 30 / 2 = 900 cm².
Diện tích tam giác ABC là 40 x 30 / 2 = 600 cm²
Diện tích của tam giác ABC là 900 - 600 = 300 cm²
b. Tỷ lệ phần trăm diện tích tam giác ABC so với tam giác ADC là (300 / 600) x 100 = 50%
Kết quả
a. Diện tích tam giác ABC là 36 cm²
Diện tích của tam giác ABC là 600 cm²
b. Tỷ lệ phần trăm diện tích tam giác ABC so với tam giác ADC là 50%
3. Một số bài tập bổ trợ
Câu 1: Trong hình chữ nhật ABCD, chia mỗi cạnh AD và BC thành 4 đoạn bằng nhau và cạnh CD thành 3 đoạn bằng nhau, sau đó nối các điểm theo như trong hình.
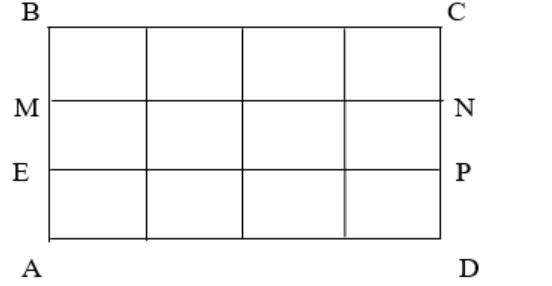
Xác định số lượng hình chữ nhật có trong hình vẽ
Giải pháp: Đầu tiên, chúng ta cần xem xét các hình chữ nhật được tạo thành từ các đoạn thẳng trên cạnh AD. Tương tự, ta áp dụng cho các đoạn trên hai cạnh AD và BC.
Chẳng hạn, ta tính số hình chữ nhật được tạo ra từ hai đoạn AB và BC, với mỗi đoạn đều có độ dài 10 cm.
Tiếp theo, chúng ta tính số hình chữ nhật được hình thành từ hai đoạn AD và MN, nối các điểm trên cạnh AD và BC, mỗi đoạn cũng có độ dài 10 cm.
Do đó, tổng số hình chữ nhật trên hình vẽ là 10 + 10 + 10 + 10 + 10 + 10 = 60 hình
Bài 2: Cần tối thiểu bao nhiêu điểm để có thể tạo ra 5 hình tứ giác khi nối các điểm lại?
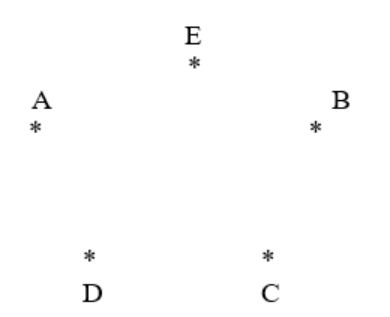
Giải đáp:
Với chỉ 4 điểm, ta chỉ có thể tạo một hình tứ giác duy nhất.
Nếu chọn 5 điểm từ các điểm A, B, C, D, E, và chọn A làm một đỉnh, ta có thể tạo ra các tứ giác bằng cách chọn thêm 3 điểm trong số 4 điểm còn lại, với A là một đỉnh.
Có 4 cách chọn ba điểm từ các điểm B, C, D, E để kết hợp với điểm A.
Như vậy, có 4 hình tứ giác với A là một đỉnh và một tứ giác không có A là đỉnh, chính là BCDE.
Vì vậy, tổng số hình tứ giác là 5.
Bài 3: Tam giác ABC có diện tích 150 cm². Nếu mở rộng đáy BC về phía B thêm 5 cm, diện tích sẽ tăng thêm 37,5 cm². Tính chiều dài của đáy BC.
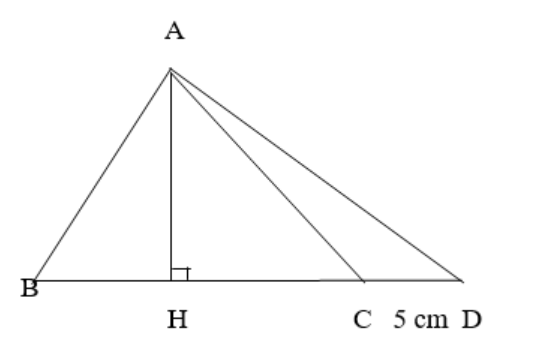
Kết quả
Cách 1: Vẽ đường cao AH từ đỉnh A của tam giác ABC, và AH cũng đồng thời là đường cao của tam giác ABD
Đoạn đường cao AH tính được là 37,5 x 2/5 = 15 cm
Chiều dài đáy BC là 150 x 2/15 = 20 cm
Kết quả cuối cùng là 20 cm
Cách 2: Vẽ đường cao AH từ đỉnh A vuông góc với BC, AH là đường cao chung của hai tam giác ABC và ABD, với tỉ số diện tích của chúng là SABC/SABD = 150/37,5 = 4
Vì tỉ số diện tích của hai tam giác là 4 và chúng cùng chung đường cao, nên tỉ số của hai đáy cũng là 4, với đáy BC tính được là 5 x 4 = 20 cm
Kết quả là 20 cm
Tham khảo Đề thi học kì 2 tiếng Việt lớp 5 có đáp án mới nhất năm 2022-2023 từ Mytour
