1. Bài 138 trong vở bài tập Toán lớp 4: Tìm hai số khi biết tổng và tỷ lệ của chúng
Câu 1. Điền số hoặc tỷ lệ phù hợp vào chỗ trống
a)
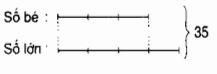
Tổng của hai số là …
Số nhỏ được biểu diễn bằng …. phần bằng nhau.
Số lớn được biểu thị bằng … phần tương tự.
Tỷ lệ giữa số nhỏ và số lớn là …. Tổng số phần bằng nhau là ….. phần.
b)

Tổng của hai số là …
Số lớn được thể hiện bằng … phần bằng nhau.
Số nhỏ được biểu diễn bằng … phần tương tự.
Tỷ lệ giữa số lớn và số nhỏ là …
Tổng số phần bằng nhau là … phần.
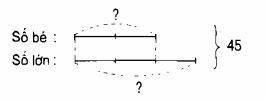
Câu 2. Tổng của hai số là 45. Tỷ lệ giữa chúng là 2/3. Xác định hai số đó.
Câu 3. Một cửa hàng đã bán 49kg gạo, trong đó số gạo nếp chiếm 2/5 tổng số gạo.
Cửa hàng đó đã bán được bao nhiêu ki-lô-gam của mỗi loại?
Giải đáp và hướng dẫn
Câu 1. Giải bài toán
Tổng hai số là 35.
Số nhỏ được thể hiện bằng 3 phần bằng nhau.
Số lớn được thể hiện bằng 4 phần tương đương.
Tỷ lệ giữa số nhỏ và số lớn là 3 : 4 hoặc 3/4.
Tổng số phần bằng nhau là 7 phần.
b) Giải bài toán
Tổng của hai số là 63.
Số lớn được thể hiện bằng 5 phần bằng nhau.
Số nhỏ được biểu diễn bằng 4 phần tương đương.
Tỷ lệ giữa số lớn và số nhỏ là 5 : 4 hoặc 5/4.
Tổng số phần bằng nhau là 9 phần.
Câu 2. Tóm tắt nội dung:
Giải pháp
Dựa trên sơ đồ, tổng số phần bằng nhau là:
2 + 3 = 5 (phần)
Số nhỏ là:
45 : 5 × 2 = 18
Số lớn là: 45 – 18 = 27
Kết quả: Số nhỏ là 18
Số lớn là: 27
Câu 3. Tóm tắt nội dung:

Giải đáp
Dựa vào sơ đồ, tổng số phần bằng nhau là:
2 + 5 = 7 (phần)
Số ki-lô-gam gạo nếp mà cửa hàng đã bán được là:
2 × 7 = 14 (kg)
Số ki-lô-gam gạo tẻ cửa hàng đã bán ra là:
49 – 14 = 35 (kg)
Kết quả: Gạo nếp 14kg
Gạo tẻ 35kg
2. Các dạng bài tập tìm số khi biết tổng và tỷ lệ của số đó
Dạng 1: Khi biết tổng và tỷ lệ của các phần
Cách giải
Bước 1: Vẽ sơ đồ dựa trên thông tin đã cho.
Bước 2: Xác định tổng số phần bằng nhau
Bước 3: Tính số nhỏ và số lớn (Có thể tính số lớn trước hoặc sau, tùy theo yêu cầu bài toán)
Số nhỏ = (Tổng : số phần bằng nhau) × số phần của số nhỏ (Hoặc Tổng - số lớn)
Số lớn = (Tổng : số phần bằng nhau) × số phần của số lớn (Hoặc Tổng - số nhỏ)
Bước 4. Đưa ra kết luận (Học sinh có thể thực hiện bước kiểm tra để đảm bảo kết quả chính xác)
Ví dụ minh họa
Ví dụ 1: Tuổi của mẹ và An tổng cộng là 36 tuổi, tuổi của mẹ gấp 7 lần tuổi của An. Hãy tính tuổi của mỗi người.
Giải thích:
Tổng số phần chia đều là:
7 cộng 2 bằng 9 (phần)
Tuổi của mẹ là:
36 chia 9 rồi nhân 7 bằng 28 (tuổi)
Tuổi của An là:
36 trừ 28 bằng 8 (tuổi)
Kết quả: Mẹ 28 tuổi; An 8 tuổi
Ví dụ 2: Tổng hai số bằng số lớn nhất có hai chữ số. Tỉ lệ của hai số là 4/5. Xác định hai số đó.
Giải pháp:
Tổng hai số là 99.
Tổng số phần chia đều là: 4 + 5 = 9 phần
Số nhỏ hơn là: 99 chia 9 nhân 4 = 44
Số lớn hơn là: 99 trừ 44 = 55
Kết quả: Số nhỏ: 44; số lớn: 55
Dạng 2: Thiếu tổng (Cho tỉ số, không có tổng số)
Phương pháp giải
Xác định tổng của hai số bằng cách chuyển về dạng tìm hai số khi biết tổng và tỉ số cơ bản (dạng 1).
Ví dụ minh họa
Ví dụ 1: Một hình chữ nhật có chu vi 200m. Chiều dài gấp 3 lần chiều rộng. Tính diện tích của hình chữ nhật?
Giải pháp:
Tổng chiều dài và chiều rộng là:
200 chia 2 = 100 (m)
Tổng số phần chia đều là:
3 cộng 2 = 5 (phần)
Giá trị của một phần là: 100 chia 5 = 20 (m)
Chiều dài của hình chữ nhật là:
20 nhân 3 = 60 (m)
Chiều rộng của hình chữ nhật là:
20 nhân 2 = 40 (m)
Diện tích của hình chữ nhật là:
60 nhân 40 = 2400 (m²)
Kết quả: 2400 (m²).
Ví dụ 2: Xác định hai số khi biết trung bình cộng của chúng là 16 và số lớn gấp 5/3 số bé.
Giải pháp:
Tổng của hai số là:
16 nhân 2 = 32
Số phần chia đều là:
5 cộng 3 = 8
Số nhỏ hơn là:
32 chia 8 nhân 3 = 12
Số lớn là:
32 trừ 12 = 20
Kết quả: Số bé: 12; số lớn: 20.
Dạng 3: Thiếu tỉ số (Cho tổng số, không cho tỉ số)
Phương pháp giải
Xác định tỉ số của hai số bằng cách đưa về dạng tìm hai số khi biết tổng và tỉ số cơ bản (dạng 1).
Ví dụ minh họa
Ví dụ 1: Có hai thùng chứa 96 lít dầu, biết rằng dung tích của thùng thứ nhất gấp 5 lần dung tích của thùng thứ hai. Mỗi thùng chứa bao nhiêu lít dầu?
Giải pháp:
Ta có: Dung tích của thùng thứ nhất gấp 5 lần thùng thứ hai.
Tức là: Dung tích của thùng thứ nhất bằng 3/5 dung tích của thùng thứ hai.
Số phần chia đều là:
3 cộng 5 = 8 (phần)
Giá trị của một phần là:
96 chia 8 = 12 (lít)
Số lít dầu trong thùng thứ nhất là:
12 nhân 3 = 36 (lít)
Số lít dầu trong thùng thứ hai là:
12 nhân 5 = 60 (lít)
Kết quả: Đoạn thứ nhất: 36 (m);
Đoạn thứ hai: 60 (m).
Ví dụ 2: Một sợi dây dài 28m được cắt thành hai đoạn, trong đó đoạn đầu dài gấp 3 lần đoạn còn lại. Tính chiều dài của mỗi đoạn.
Giải pháp: Vì đoạn đầu dài gấp 3 lần đoạn còn lại, nên đoạn còn lại dài bằng 1/3 đoạn đầu.
Số phần chia đều là:
1 cộng 3 = 4 (phần)
Chiều dài của đoạn đầu là:
28 chia 4 = 7 (m)
Chiều dài của đoạn còn lại là:
28 chia 4 nhân 3 = 21 (m)
Kết quả: Đoạn đầu: 7 (m);
Đoạn còn lại: 21 (m)
Ví dụ 3: Tổng của hai số là 72. Tìm hai số biết rằng nếu giảm số lớn xuống 5 lần thì thu được số bé.
Giải pháp: Vì nếu số lớn giảm 5 lần thì trở thành số bé, nên số bé bằng 1/5 số lớn.
Số phần chia đều là:
1 cộng 5 = 6 (phần)
Số lớn là:
72 chia 6 nhân 5 = 60
Số bé là:
72 trừ 60 = 12
Kết quả: Số bé: 12; số lớn: 60
Dạng 4: Ẩn cả tổng và tỉ số 1.
Cách giải
Xác định tổng và tỉ số của hai số, đưa về bài toán tìm hai số khi biết tổng và tỉ số cơ bản (dạng 1).
Ví dụ cụ thể
Ví dụ 1: Tìm hai số nguyên, biết rằng trung bình cộng của chúng là 120 và 1/3 số đầu tiên bằng 1/7 số thứ hai.
Cách giải:
Tổng hai số là:
120 × 2 = 240
1/3 số đầu tiên bằng 1/7 số thứ hai, nên số đầu tiên bằng 3/7 số thứ hai.
Tổng số phần chia đều là:
3 + 7 = 10 (phần)
Số đầu tiên là:
240 : 10 × 3 = 72
Số thứ hai là:
240 – 72 = 168
Kết quả: Số đầu tiên: 72; số thứ hai: 168
Ví dụ 2: Một số tự nhiên, khi thêm chữ số 0 vào cuối, sẽ tạo ra một số mới. Trung bình cộng của số mới và số cũ là 132. Xác định số đó.
Lời giải: Tổng của số mới và số cũ là:
132 × 2 = 264
Khi thêm chữ số 0 vào cuối số cần tìm, ta được số mới, gấp 10 lần số cần tìm. Vì vậy, số cần tìm là 1 phần và số mới là 10 phần.
Theo sơ đồ, tổng số phần là:
1 + 10 = 11 (phần)
Số tự nhiên cần tìm là:
264 : 11 = 24
Kết quả: 24
3. Một số bài tập khác
Bài 1: Tổng của hai số là 96 và tỉ số của chúng là 3/5. Xác định hai số này.
Bài 2: Minh và Khôi có tổng cộng 25 quyển vở. Số vở của Minh là 2/3 số vở của Khôi. Tính số vở của mỗi bạn.
Bài 3: Tổng của hai số là 333, và tỉ số của chúng là 2/7. Tìm hai số này.
Bài 4: Hai kho chứa tổng cộng 125 tấn thóc. Kho thứ nhất có số thóc gấp 3/2 kho thứ hai. Xác định số thóc ở mỗi kho.
Bài 5: Một miếng vườn hình chữ nhật với chu vi 200m, chiều dài gấp 3 lần chiều rộng. Tính diện tích của miếng vườn.
Bài 6: Miếng đất hình chữ nhật có chu vi 240m, với chiều rộng bằng 2/3 chiều dài. Tính diện tích của miếng đất.
