Bài 63 trong vở bài tập Toán lớp 4: Nhân với số ba chữ số (phần tiếp theo)

1. Kiến thức cơ bản về phép nhân

Phép nhân là phép toán cơ bản dùng để tính tổng của nhiều số tự nhiên thông qua việc cộng lặp lại. Ký hiệu của phép nhân có thể là dấu “x” hoặc dấu “.”. Ví dụ: a x b = c, trong đó a và b là các thừa số và c là tích. Một số đặc điểm của phép nhân gồm:

- Tính chất giao hoán: Khi thay đổi vị trí các thừa số trong phép nhân, kết quả không thay đổi. → a x b = b x a

- Tính chất kết hợp: Khi nhân một số tự nhiên với tích của hai số khác, chúng ta có thể thực hiện phép nhân giữa số đó với từng thừa số trước rồi nhân kết quả với số còn lại. → (a x b) x c = a x (b x c)

- Tính chất nhân với số 0: Bất kỳ số tự nhiên nào nhân với 0 đều cho kết quả là 0. → a x 0 = 0 x a = 0

- Tính chất nhân với số 1: Bất kỳ số tự nhiên nào khi nhân với 1 thì vẫn giữ nguyên giá trị đó. → a x 1 = 1 x a = a

- Nhân số với tổng: Khi nhân một số tự nhiên với tổng của hai số, chúng ta có thể nhân số đó với từng số hạng và cộng các kết quả lại. → a x (b + c) = a x b + a x c

- Nhân số với hiệu: Khi nhân một số tự nhiên với hiệu của hai số, chúng ta có thể nhân số đó với số bị trừ và số trừ rồi lấy kết quả của phép trừ giữa chúng. → a x (b – c) = a x b – a x c

Khi một thừa số trong tích được nhân lên n lần và một thừa số khác bị chia đi n lần, thì tích của phép nhân sẽ không thay đổi. Nếu chỉ một thừa số trong tích được nhân lên n lần, các thừa số còn lại giữ nguyên thì tích sẽ tăng lên n lần. Ngược lại, nếu một thừa số bị chia đi n lần, các thừa số còn lại giữ nguyên thì tích cũng giảm đi n lần. Nếu một thừa số được nhân lên n lần và một thừa số khác được nhân lên m lần, thì tích sẽ được nhân lên (m × n) lần. Ngược lại, nếu một thừa số bị chia đi m lần và một thừa số khác bị chia đi n lần, thì tích sẽ giảm đi (m × n) lần. Nếu một thừa số tăng thêm a đơn vị, tích sẽ tăng thêm a lần tích của các thừa số còn lại. Tích sẽ là số chẵn nếu có ít nhất một thừa số là số chẵn. Nếu có ít nhất một thừa số là số tròn chục hoặc có chữ số tận cùng là 5 và ít nhất một thừa số chẵn, tích sẽ có chữ số tận cùng là 0. Nếu tất cả các thừa số đều lẻ và có ít nhất một thừa số có chữ số tận cùng là 5, thì tích sẽ có chữ số tận cùng là 5.

2. Kiến thức về nhân số có ba chữ số

Để hiểu rõ phương pháp nhân với số có ba chữ số, chúng ta cần áp dụng phương pháp nhân cơ bản qua ba bước: nhân hàng đơn vị, hàng chục và hàng trăm. Sau đây là các bước thực hiện cụ thể:

Bước 1: Nhân hàng đơn vị: Lấy chữ số hàng đơn vị của số có ba chữ số và nhân với từng chữ số của số cần nhân. Ghi kết quả vào hàng đơn vị của kết quả cuối cùng và phần dư (nếu có) để tiếp tục ở bước sau.

Bước 2: Nhân hàng chục: Lấy chữ số hàng chục của số có ba chữ số và nhân với từng chữ số của số cần nhân. Ghi kết quả vào hàng chục của kết quả cuối cùng và phần dư (nếu có) để tiếp tục ở bước sau.

Bước 3: Nhân với hàng trăm: Lấy chữ số hàng trăm của số ba chữ số và nhân với từng chữ số của số cần nhân. Ghi kết quả vào hàng trăm của số kết quả cuối cùng. Nếu có phần dư, ghi kết quả vào hàng trăm của phần dư để sử dụng cho bước tiếp theo. Sau khi thực hiện các bước trên, cộng tất cả các hàng để có tổng của phép nhân. Ví dụ: Tính 234 nhân với 567.

1404 (234 x 7)

1170 (234 x 6, dịch sang trái một chữ số)

1404 (234 x 5, dịch sang trái hai chữ số)

132678 (Tổng) Kết quả cuối cùng là 132678.

Đây là phương pháp cơ bản để nhân một số với ba chữ số. Bạn có thể áp dụng quy trình tương tự cho các bài toán khác bằng cách thay đổi giá trị của các số cần nhân.

Ví dụ 1. 164 x 123 = ?

a) Tính như sau: 164 x 123 = 164 x (100 + 20 + 3) = 16400 + 3280 + 492 = 20172

b) Thực hiện phép tính như sau:

Nhân với số ba chữ số: 3 nhân 4 bằng 12, viết 2 nhớ 1; 3 nhân 6 bằng 18, cộng 1 bằng 19, viết 9 nhớ 1; 3 nhân 1 bằng 3, cộng 1 bằng 4, viết 4. 2 nhân 4 bằng 8, viết 8 (dưới 9); 2 nhân 6 bằng 12, viết 2 nhớ 1; 2 nhân 1 bằng 2, cộng 1 bằng 3, viết 3. 1 nhân 4 bằng 4, viết 4 (dưới 2); 1 nhân 6 bằng 6, viết 6; 1 nhân 1 bằng 1, viết 1. Hạ 2, 9 cộng 8 bằng 17, viết 7 nhớ 1; 4 cộng 2 bằng 6, 6 cộng 4 bằng 10, cộng 1 bằng 11, viết 1 nhớ 1; 3 cộng 6 bằng 9, cộng 1 bằng 10, viết 0 nhớ 1; 1 cộng 1 bằng 2, viết 2.

c) Trong phương pháp tính trên: 492 là tích riêng đầu tiên. 328 là tích riêng thứ hai, được lùi một cột vì tương ứng với 3280. 164 là tích riêng thứ ba, được lùi hai cột vì tương ứng với 16400.

Ví dụ 2. 258 x 203 = ?

a) Thực hiện phép nhân, ta có: 258 x 203 = ....

b) Tích riêng thứ hai toàn là chữ số 0. Thường thì tích riêng này không cần viết ra, mà chỉ ghi gọn như sau: Nhân với số ba chữ số.

Chú ý: Viết tích riêng 516 lùi hai cột so với tích riêng đầu tiên.

3. Vở bài tập Toán lớp 4, bài 63: Nhân với số ba chữ số (phần tiếp theo)

Vở bài tập Toán lớp 4, bài 63, trang 73 - Câu 1

Đặt tính và tính toán

235 x 503

307 x 653

Phương pháp giải: Đặt sao cho các chữ số cùng một hàng thẳng cột nhau

Lưu ý: Nếu tích riêng thứ hai toàn là số 0, ta thường bỏ qua nó; tích riêng thứ ba sẽ được lùi hai cột so với tích riêng đầu tiên

Đáp án:

235 x 503 = 118205

307 x 653 = 200471

Vở bài tập Toán lớp 4, bài 63, trang 73, Câu 2

Ghi Đ nếu đúng, ghi S nếu sai

Phương pháp giải: Đặt các chữ số sao cho chúng thẳng hàng và cùng cột

Lưu ý: Nếu tích riêng thứ hai chỉ chứa số 0, chúng ta thường không ghi nó. Tích riêng thứ ba cần được lùi hai cột so với tích riêng đầu tiên

Đáp án:

Vở bài tập Toán lớp 4, bài 63, trang 73, Câu 3

Điền số phù hợp vào chỗ trống

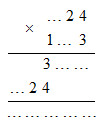
Hướng dẫn giải: Sử dụng các chữ số đã có, suy luận để điền các chữ số còn thiếu vào chỗ trống

Giải đáp:

124 x 103 = 12772

Vở bài tập Toán lớp 4, bài 63, trang 73, Câu 4

Diện tích của khu đất hình chữ nhật có chiều dài 125m và chiều rộng 105m là bao nhiêu?

Cách tính: Diện tích khu đất hình chữ nhật = chiều dài nhân với chiều rộng

Tóm tắt nội dung:

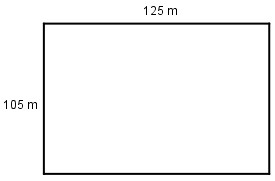
Kết quả: Bài giải

Diện tích của hình chữ nhật là:

125 nhân với 105 bằng 13125 (m2)

Kết quả là: 13125 m2