Bài tập Hình học lớp 7 về các trường hợp bằng nhau của tam giác

Buzz

Nội dung bài viết

Mục tiêu học tập

Các tài liệu hỗ trợ

Các trường hợp bằng nhau của hai tam giác

IV. Các trường hợp bằng nhau của 2 tam giác vuông

V. Ứng dụng các trường hợp bằng nhau của tam giác

VI. Bài tập về hai tam giác bằng nhau

Xem thêm

Đọc tóm tắt

- Tổng hợp kiến thức về các trường hợp bằng nhau của tam giác, cung cấp ví dụ và bài tập tự luyện.
- Mytour giới thiệu các trường hợp bằng nhau của hai tam giác với đa dạng bài tập và đáp án.
- Mục tiêu học tập là áp dụng kiến thức vào việc chứng minh sự bằng nhau giữa hai tam giác và các yếu tố khác.
- Các trường hợp bằng nhau của hai tam giác bao gồm cạnh.
- cạnh.
- cạnh, cạnh.
- góc.
- cạnh, góc.
- cạnh.
- góc.
- Ứng dụng các trường hợp bằng nhau để chứng minh, tính toán và so sánh trong các bài toán hình học.
- Bài tập thực hành với nhiều trường hợp khác nhau để rèn luyện kỹ năng giải toán và áp dụng kiến thức.

Tổng hợp kiến thức về các trường hợp bằng nhau của tam giác, cung cấp ví dụ minh họa và bài tập tự luyện.

Mytour giới thiệu các trường hợp bằng nhau của hai tam giác với đa dạng bài tập và đáp án, giúp học sinh chuẩn bị cho kỳ thi một cách tốt nhất.

Mục tiêu học tập

Học sinh sẽ có khả năng áp dụng kiến thức sau khi học chuyên đề này.

1. Áp dụng các trường hợp bằng nhau của tam giác để chứng minh sự bằng nhau giữa hai tam giác; Thực hiện các bước chứng minh sự bằng nhau giữa hai đoạn thẳng hoặc hai góc; Sử dụng đường phụ để tạo ra hai tam giác bằng nhau.

2. Hiểu các bước phân tích bài toán và xác định hướng chứng minh.

3. Sử dụng kỹ năng để áp dụng kiến thức đã học vào việc giải các bài toán.

Các tài liệu hỗ trợ

- Bài tập nâng cao và một số chuyên đề toán lớp 7

- Khóa học Hình học cao cấp cho học sinh trung học cơ sở

- Sử dụng yếu tố phụ để giải các bài toán hình học lớp 7 một cách chính xác

- Chương trình bồi dưỡng kiến thức toán lớp 7

- Làm giàu kiến thức và phát triển nâng cao kỹ năng giải toán lớp 7

Các trường hợp bằng nhau của hai tam giác

1. Điều cần ghi nhớ

Chúng ta đã biết rằng nếu hai tam giác bằng nhau thì các cặp cạnh tương ứng và các cặp góc tương ứng sẽ bằng nhau. Đó là lợi ích của việc chứng minh hai tam giác bằng nhau.

*. Để chứng minh hai đoạn thẳng (hoặc hai góc) bằng nhau, chúng ta thường thực hiện các bước sau:

- Xác định xem hai đoạn thẳng (hoặc hai góc) thuộc hai tam giác nào.

- Chứng minh rằng hai tam giác đó là bằng nhau.

- Kết luận hai cạnh (hoặc hai góc) tương ứng là bằng nhau.

*. Để tạo ra hai tam giác bằng nhau, có thể chúng ta phải vẽ thêm đường phụ bằng nhiều cách sau:

- Kết nối hai cạnh có sẵn trên hình để tạo ra một cạnh chung của hai tam giác.

- Trên một tia đã cho, vẽ một đoạn thẳng có độ dài bằng một đoạn thẳng khác.

- Từ một điểm đã cho, vẽ một đường thẳng song song với một đoạn thẳng.

- Từ một điểm đã cho, vẽ một đường thẳng vuông góc với một đoạn thẳng.

Cũng có nhiều cách khác mà chúng ta có thể tích luỹ kinh nghiệm khi giải các bài toán.

2. Các trường hợp bằng nhau của tam giác

a) Trường hợp 1: cạnh – cạnh – cạnh:

a) Trường hợp 1: cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó là bằng nhau.

b) Trường hợp 2: cạnh – góc – cạnh: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó là bằng nhau.

c) Trường hợp 3: góc – cạnh – góc: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó là bằng nhau.

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó là bằng nhau.

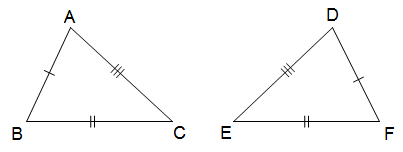
AB = DF (đều cho trước)

AC = DE (đều cho trước)

BC = EF (đều cho trước)

Kết luận ∆ABC = ∆DFE (c - c - c)

$\Rightarrow \widehat{A} = \widehat{D};\widehat{B} = \widehat{F};\widehat{C} = \widehat{F}$

b) Trường hợp 2: cạnh – góc – cạnh:

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó là bằng nhau.

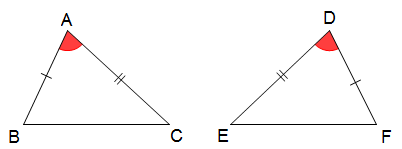
+ Kiểm tra ∆ABC và ∆DFE:

AB = DF (đều cho trước)

$\widehat{A}=\widehat{D}$

AC = DE (đều cho trước)

Kết luận ∆ABC = ∆DFE (c - g - c)

$\Rightarrow\widehat{B}=\widehat{F};\widehat{C}=\widehat{E}$

Ghi chú: Hai cặp góc bằng nhau phải xen giữa hai cặp cạnh bằng nhau mới có thể kết luận hai tam giác bằng nhau.

c) Trường hợp 3: góc – cạnh – góc:

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó là bằng nhau.

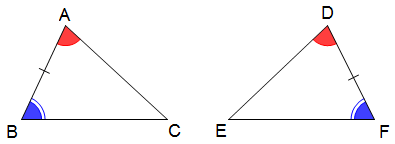
+ Kiểm tra ∆ABC và ∆DFE:

$\widehat{A}=\widehat{D}$

AB = DF (đều cho trước)

$\widehat{B}=\widehat{F}$

Kết luận ∆ABC = ∆DFE (g - c - g)

$\Rightarrow\widehat{C}=\widehat{E}$

Ghi chú:

- Hai cặp cạnh bằng nhau phải tạo thành hai cặp góc bằng nhau mới có thể kết luận hai tam giác bằng nhau.

- Khi hai tam giác đã được chứng minh bằng nhau, chúng ta có thể suy ra các yếu tố tương ứng còn lại cũng bằng nhau.

IV. Các trường hợp bằng nhau của 2 tam giác vuông

* Trường hợp cạnh góc vuông - cạnh góc vuông (cgv - cgv): Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

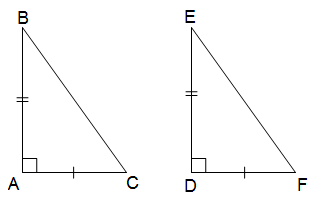
* Trường hợp cạnh góc vuông - góc nhọn (cgv - gn): Nếu một cạnh góc vuông và một góc nhọn kề cạnh đó của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh tương ứng của tam giác vuông kia thì hai tam giác vuông đó là bằng nhau.

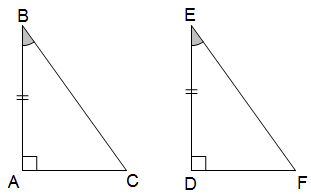
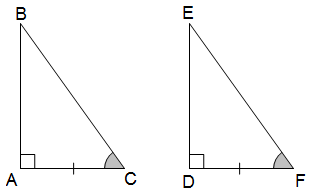
* Trường hợp cạnh huyền - góc nhọn (ch - gn): Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn tương ứng của tam giác vuông kia thì hai tam giác vuông đó là bằng nhau.

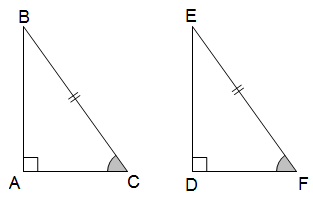
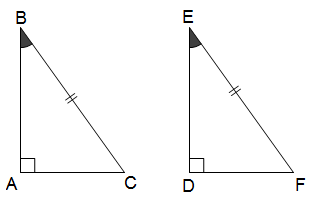
V. Ứng dụng các trường hợp bằng nhau của tam giác

Chúng ta thường áp dụng các trường hợp bằng nhau của tam giác để:

- Chứng minh: hai tam giác bằng nhau, hai đoạn thẳng bằng nhau, hai góc bằng nhau; hai đường thẳng vuông góc; hai đường thẳng song song; ba điểm thẳng hàng; ...

- Tính: tính độ dài các đoạn thẳng; tính số đo của các góc; tính chu vi; diện tích; ...

- So sánh: so sánh độ dài các đoạn thẳng; so sánh các góc; ...

VI. Bài tập về hai tam giác bằng nhau

Bài 1: Trong tam giác ABC, điểm M là trung điểm của BC và điểm N nằm trong tam giác sao cho NB = NC.

Chứng minh: Tam giác NMB bằng tam giác NMC.

Bài 2: Trong tam giác ABC, có AB = AC. Kẻ đường phân giác AE của góc BAC (E nằm trên BC). Chứng minh rằng: Góc ABE = Góc ACE.

Bài 3: Cho tam giác ABC có góc A = 40°, AB = AC. Gọi M là trung điểm của BC. Tính các góc của tam giác AMB và tam giác AMC.

Bài 4: Trong tam giác ABC có AB = AC. D, E nằm trên cạnh BC sao cho BD = DE = EC. Biết AD = AE.

a. Chứng minh góc EAB = góc DAC.

b. Gọi M là trung điểm của BC. Chứng minh rằng AM là đường phân giác của góc DAE.

c. Giả sử góc DAE = 60°. Tính các góc còn lại của tam giác DAE.

Bài 5: Trong tam giác ABC, có góc A = 90°. Vẽ đường thẳng AD vuông góc với AB (D, C nằm ở phía ngược với AB) và AD = AB. Vẽ đường thẳng AE vuông góc với AC (E, B nằm ở phía ngược với AC) và AE = AC. Biết DE = BC. Tính góc BAC.

Bài 6: Trong tam giác ABC, có AB = AC. Kẻ đường phân giác AE của góc BAC (E thuộc BC). Chứng minh rằng:

a. Tam giác ABE = tam giác ACE

b. Đường AE là đường trung trực của đoạn thẳng BC.

Bài 7: Trong tam giác ABC với AB < AC, kẻ tia phân giác AD của góc BAC (D thuộc BC). Trên cạnh AC, lấy điểm E sao cho AE = AB, trên tia AB, lấy điểm F sao cho AF = AC. Chứng minh rằng:

a. Tam giác BDF = tam giác EDC.

b. BF = EC.

c. F, D, E thẳng hàng.

d. AD vuông góc với FC

Bài 8: Trong góc nhọn xOy, trên tia Ox, lấy 2 điểm A và C. Trên tia Oy, lấy 2 điểm B và D sao cho OA = OB; OC = OD. (A nằm giữa O và C; B nằm giữa O và D).

a. Chứng minh tam giác OAD = tam giác OBC

b. So sánh 2 góc CAD và CBD.

Bài 9: Trong tam giác ΔABC vuông ở A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.

a. Chứng minh tam giác ΔABC = tam giác ΔABD

b. Trên tia đối của tia AB, lấy điểm M. Chứng minh tam giác MBD = tam giác MBC.

Bài 10: Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kì. Chứng minh:

a. Tam giác AOI = tam giác BOI.

b. AB vuông góc OI.

Bài 11: Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm E sao cho ME = MA.

a. Chứng minh tam giác ACB // tam giác BEC.

b. Gọi I là một điểm trên AC, K là một điểm trên EB sao cho AI = EK. Chứng minh rằng 3 điểm I, M, K thẳng hàng.

Bài 12: Cho tam giác ABC; M là trung điểm của BC; N là 1 điểm trong tam giác sao cho NB = NC. Chứng minh: ∆ NMB = ∆ NMC.

Bài 13. Cho tam giác ABC có AB = AC. Kẻ AE là phân giác của góc (E thuộc BC). Chứng minh rằng: ∠ DABE = ∠ DACE

Bài 14. Cho tam giác ABC có góc A = 40° , AB = AC. Gọi M là trung điểm của BC. Tính các góc của tam giác AMB và tam giác AMC.

Bài 15. Cho tam giác ABC (AB < AC) có AM là phân giác của góc A (M thuộc BC). Trên AC lấy D sao cho AD = AB.

a. Chứng minh tam giác BDM là tam giác đều.

b. Gọi K là giao điểm của AB và DM. Chứng minh DDAK = DBAC

Bài 16. Cho tam giác ABC vuông ở C, có góc A bằng 600, tia phân giác của góc BAC cắt BC ở E. Kẻ Ek vuông góc với AB (K thuộc AB), kẻ BD vuông góc với AE (D thuộc AE). Chứng minh:

a. AK = KB

b. AD = BC

Bài 17. Cho tam giác ABC. Qua A kẻ đường thẳng song song với BC, qua C kẻ đường thẳng song song với AB. Hai đường thẳng cắt nhau tại D.

a. Chứng minh tam giác DABC đồng dạng tam giác DADC

b. Chứng minh tam giác DADB đồng dạng tam giác DCBD

c. Gọi O là giao điểm của AC và BD. Chứng minh tam giác DABO đồng dạng tam giác DCOD

Bài 18. Cho góc xAy khác góc bẹt. Gọi AD là tia tia phân giác của góc xAy. Qua D kẻ đường thẳng vuông góc với Ay cắt Ay tại C và cắt Ax tại E. Qua D kẻ đường thẳng vuông góc với Ax cắt Ax tại B và cắt Ay tại H. Chứng minh:

a. DABD = DACD

b. DDBE = DDCH

c. DABH = DACE

Bài 19. Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và D. Trên tia Oy lấy hai điểm C và E sao cho OD = OE và OA = OB.

a. Chứng minh DODC = DOBE

b. Gọi A là giao điểm của BE và CD. Chứng minh DAOB = DAOC

c. Chứng minh BC vuông góc với OA

Bài 20 : Cho tam giác ABC vuông tại A. tia phân giác của góc ABC cắt AC tại D. lấy E trên cạnh BC sao cho BE = AB.

a) Chứng minh : Δ ABD = Δ EBD.

b) Tia ED cắt BA tại M. chứng minh : EC = AM

c) Nối AE. Chứng minh : góc AEC = góc EAM.

Bài 21: Cho tam giác ABC vuông góc tại A có góc B = 530.

a) Tính góc C.

b) Trên cạnh BC, lấy điểm D sao cho BD = BA. Tia phân giác của góc B cắt cạnh AC ở điểm E. Chứng minh : ΔBEA = ΔBED.

c) Qua C, vẽ đường thẳng vuông góc với BE tại H. CH cắt đường thẳng AB tại F. CMR : ΔBHF = ΔBHC.

d) Chứng minh: ΔBAC = ΔBDF và D, E, F thẳng hàng.

Bài 22: Cho tam giác ABC (AB <AC). Tia phân giác của góc A cắt đường trung trực của BC tại I. kẻ IH vuông góc AB tại H. IK vuông góc AC tại K.

a/ Chứng minh : BH = CK.

b/ Chứng minh AHIK nội tiếp đường tròn và tÌm tâm đườn tròn đó

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]

Các câu hỏi thường gặp

Các trường hợp bằng nhau của hai tam giác là gì?

Có ba trường hợp bằng nhau của hai tam giác: cạnh-cạnh-cạnh, cạnh-góc-cạnh và góc-cạnh-góc. Mỗi trường hợp yêu cầu các yếu tố như cạnh hoặc góc tương ứng phải bằng nhau giữa hai tam giác.

Cách chứng minh hai tam giác bằng nhau trong hình học là gì?

Để chứng minh hai tam giác bằng nhau, cần xác định các cặp cạnh và góc tương ứng. Sau đó, áp dụng các trường hợp như cạnh-cạnh-cạnh, cạnh-góc-cạnh, hoặc góc-cạnh-góc để chứng minh sự bằng nhau.

Khi nào hai tam giác vuông được coi là bằng nhau?

Hai tam giác vuông được coi là bằng nhau khi các cạnh góc vuông tương ứng bằng nhau hoặc khi một cạnh góc vuông và góc nhọn tương ứng bằng nhau, hoặc khi cạnh huyền và một góc nhọn tương ứng bằng nhau.

Cách sử dụng đường phụ để tạo ra hai tam giác bằng nhau là gì?

Để tạo ra hai tam giác bằng nhau, có thể vẽ thêm đường phụ như vẽ một đoạn thẳng song song hoặc vuông góc với một đoạn thẳng đã cho, hoặc tạo cạnh chung giữa hai tam giác.

Tại sao việc chứng minh hai tam giác bằng nhau lại quan trọng trong hình học?

Chứng minh hai tam giác bằng nhau giúp xác định các yếu tố tương ứng như cạnh và góc cũng bằng nhau, từ đó có thể giải quyết các bài toán hình học phức tạp và tính toán các đại lượng liên quan.

Làm sao để chứng minh hai đoạn thẳng hoặc hai góc bằng nhau?

Để chứng minh hai đoạn thẳng hoặc hai góc bằng nhau, cần chứng minh rằng hai tam giác có các cạnh và góc tương ứng bằng nhau, từ đó suy ra sự bằng nhau của đoạn thẳng hoặc góc.

Cách áp dụng các trường hợp bằng nhau của tam giác trong bài toán hình học là gì?

Khi giải các bài toán hình học, các trường hợp bằng nhau của tam giác giúp chứng minh sự bằng nhau của các yếu tố như đoạn thẳng, góc, hoặc các đường thẳng vuông góc, song song.

Có những bài tập nào liên quan đến các trường hợp bằng nhau của tam giác?

Các bài tập về các trường hợp bằng nhau của tam giác thường yêu cầu chứng minh sự bằng nhau của các tam giác thông qua các trường hợp như cạnh-cạnh-cạnh, cạnh-góc-cạnh, hoặc góc-cạnh-góc.