1. Bài tập hình học nâng cao lớp 5 với hướng dẫn giải chi tiết nhất
Bài 1:
Xét tam giác ABC. Trên cạnh BC, chọn điểm I sao cho IB = IC. Nối AI, chọn điểm M trên AI sao cho MI = 1/2 AM. Nối và kéo dài CM cắt cạnh AB tại N. So sánh diện tích của hai tam giác AMN và BMN.
(Dựa trên đề thi học sinh giỏi Toán cấp Tỉnh An Giang khoảng năm 1983-1984)
Giải pháp
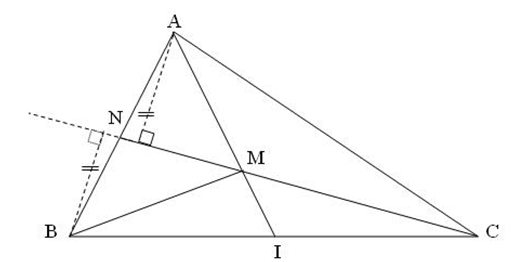
Chúng ta có SMIC = 1/2 SMCA (do hai tam giác có IM = 1/2 AM và cùng chung một đường cao từ C).
SMIC = SMIB (do hai tam giác có IB = IC và cùng chung một đường cao từ M).
Ta có: SAMC = SBMC (vì SBMC = SMIC + SMIB).
Hai tam giác AMC và BMC cùng có cạnh đáy MC, do đó, hai đường cao từ A và B xuống MC là bằng nhau.
Hai đường cao này chính là các đường cao của hai tam giác AMN và BMN, mà hai tam giác này có cạnh đáy chung là MN.
Vì vậy: SAMN = SBM
Bài 2:
Cho tam giác ABC. Trên cạnh AC, chọn điểm N sao cho NA < NC. Tìm điểm M trên BC sao cho đoạn thẳng NM chia tam giác ABC thành hai phần có diện tích bằng nhau?
Hướng dẫn cách giải
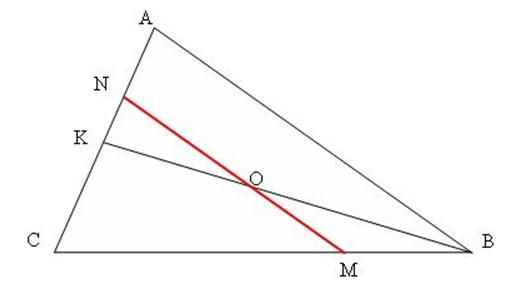
Nếu N là trung điểm của AC, thì đoạn NB (hoặc KB) sẽ chia tam giác ABC thành hai tam giác có diện tích bằng nhau. Vì NA < NC, nên điểm M cần phải nằm trên BC.
Dựa vào hình vẽ, ta cần xác định điểm M trên BC sao cho khi kết hợp NM và KB với hai cạnh còn lại của ABC, ta có hai tam giác nhỏ có diện tích bằng nhau. Điểm M chính là điểm cần tìm.
Giải pháp
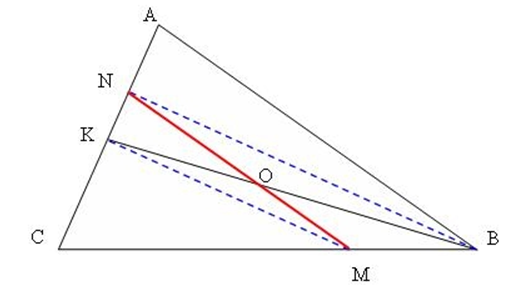
Chọn K là trung điểm của AC và nối BK.
Ta có SABK = SCBK (vì K là trung điểm của AC) => SABK = 1/2 SABC
Từ K, kẻ đoạn thẳng song song với NB, cắt BC tại M.
Trong hình thang NBMK, hai tam giác NOK và BOM có diện tích bằng nhau.
(SNBK = SNBM ; SNOK = SNBK – SNBO ; SBOM = SNBM – SNBO => SNOK = SBOM)
Tứ giác ABMN có: SABMN = SABK + SBOM – SNOK = SABK = SABC
Vậy điểm M chính là điểm cần tìm.
Bài 3:
Một miếng vườn trồng cây ăn trái có chiều dài 25m, chiều rộng bằng 3/5 chiều dài. Trong vườn có 2 lối đi rộng 1m mỗi lối (như hình vẽ). Tính diện tích còn lại để trồng cây?
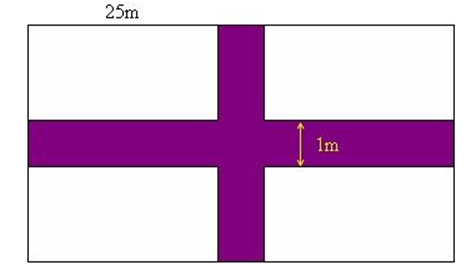
Chiều rộng của miếng vườn là: 25 : 5 x 3 = 15 (m)
Chiều dài mỗi lối đi nhỏ là: (25 - 1) : 2 = 12 (m)
Chiều rộng mỗi lối đi nhỏ là: (15 - 1) : 2 = 7 (m)
Diện tích phần còn lại để trồng cây là: 12 x 7 x 4 = 336 (m²)
Kết quả: 336 mét vuông
Cách 2:
Chiều rộng của miếng vườn là: 25 : 5 x 3 = 15 (m)
Tổng diện tích của miếng vườn là: 25 x 15 = 375 (m²)
Diện tích lối đi theo chiều dài là: 25 x 1 = 25 (m²)
Diện tích lối đi theo chiều rộng là: 15 x 1 - 1 = 14 (m²)
Diện tích đất còn lại để trồng cây là: 375 - (25 + 14) = 336 (m²)
Kết quả: 336 mét vuông
Cách 3:
Giả sử ta di chuyển 2 lối đi ra sát rìa miếng vườn, lúc này lối đi sẽ tạo thành hình chữ L (như trong hình) và phần đất còn lại sẽ trở thành một hình chữ nhật hoàn chỉnh.
Chiều rộng miếng vườn là: 25 : 5 x 3 = 15 (m)
Chiều rộng phần đất còn lại là: 15 - 1 = 14 (m)
Chiều dài phần đất còn lại là: 25 - 1 = 24 (m)
Diện tích phần đất còn lại để trồng cây là:
24 x 14 = 336 (m²)
Kết quả: 336 mét vuông
2. Toán nâng cao lớp 5 - Bài tập về thay đổi kích thước hình
Ví dụ 1: Một miếng bìa hình bình hành có chu vi 2m. Nếu giảm mỗi cạnh đi 20cm, ta sẽ có miếng bìa hình thoi với diện tích 6 dm². Tìm diện tích của miếng bìa hình bình hành ban đầu.
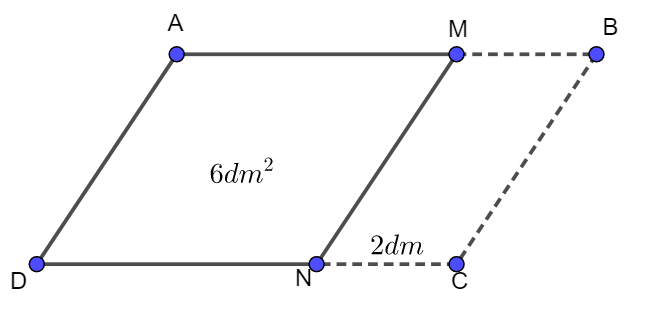
Phân tích và xác định hướng giải quyết:
Trước tiên, cần lưu ý rằng các kích thước trong bài chưa cùng đơn vị đo. Nên chuyển đổi về đơn vị đề-xi-mét để tiện cho việc tính toán.
Chu vi của hình thoi AMND có thể tính được từ chu vi của hình bình hành ABCD và các đoạn MB, NC đã biết.
Hình thoi có bốn cạnh bằng nhau. Khi biết chu vi, ta có thể tính được độ dài của mỗi cạnh.
Tính được chiều cao của hình thoi AMND, đây chính là chiều cao từ A của hình bình hành ABCD. Từ đó, ta có thể tính diện tích của hình thoi.
Giải pháp:
Chuyển đổi 2m = 20dm; 20cm = 2dm
Độ dài cạnh của hình thoi là:
(20 – 2 – 2) : 4 = 4 (dm)
Chiều cao từ điểm A xuống đoạn CD là:
6 chia 4 bằng 1,5 dm
Độ dài cạnh AB là: 4 cộng 2 bằng 6 dm
Tính diện tích hình bình hành ABCD:
1,5 nhân 6 bằng 9 dm²
Ví dụ 2. Hình thang ABCD có đáy nhỏ AB dài 10 cm và diện tích là 210 cm². Kéo dài đáy lớn CD về phía C thêm 8 cm, diện tích tăng thêm 60 cm². Tính chiều dài đáy lớn CD.
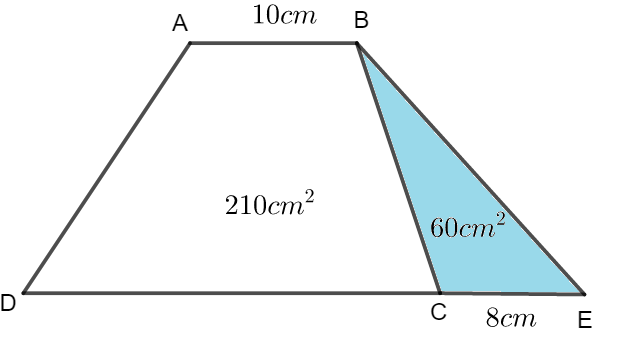
Phân tích để tìm hướng giải quyết:
Chúng ta có thể thấy rằng chiều cao của hình thang ABCD chính là chiều cao từ B xuống cạnh CE của tam giác BCE. Tính chiều cao này rồi áp dụng công thức để tìm độ dài đáy lớn.
Giải pháp:
Chiều cao từ B của tam giác BCE (cũng là chiều cao của hình thang ABCD) là: 2 x 60 chia 8 bằng 15 cm
Tổng hai đáy của hình thang ABCD được tính như sau:
210 nhân 2 chia 15 bằng 28 cm
Chiều dài của đáy lớn CD là:
28 trừ 10 bằng 18 cm
Kết quả là: 18 cm
Ví dụ 3. Cô Trâm trồng hoa trên một thửa ruộng hình thang vuông với đáy lớn dài 160m và chiều cao 30m. Khi mở rộng thửa ruộng thành mảnh đất hình chữ nhật nhưng giữ nguyên đáy lớn, diện tích thửa ruộng tăng thêm 600m². Tính số tiền cô Trâm thu được từ việc bán hoa, biết rằng mỗi hecta hoa bán được 140 triệu đồng.
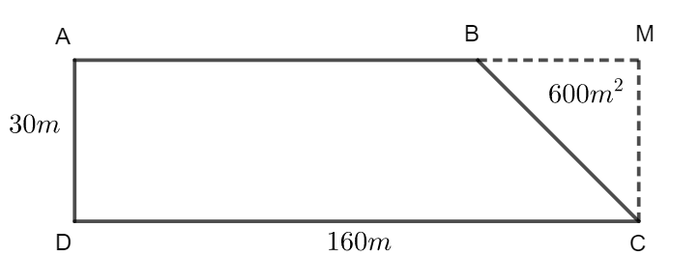
Phân tích để tìm hướng giải quyết.
Để tính số tiền bán hoa của cô Trâm, trước tiên cần tính diện tích thửa ruộng hình thang ABCD. Để tìm diện tích, chúng ta cần xác định chiều dài đáy nhỏ AB. Độ dài của AB được tính bằng cách lấy AM trừ BM, trong đó AM là chiều dài của hình chữ nhật AMCD và BM cần được xác định.
Vì ABCD là hình thang vuông, nên AD là chiều cao của hình thang và cũng chính là chiều cao của tam giác MCB từ điểm C. Dựa vào đó, tính được BM.
Giải pháp:
Chiều dài đoạn BM tính được là:
600 nhân 2 chia 30 bằng 40 m
Chiều dài đáy nhỏ AB là: 160 trừ 40 bằng 120 m
Diện tích của hình thang được tính như sau:
(120 cộng 160) nhân 30 chia 2 bằng 4200 m²
4200 m² tương đương với 0,42 ha.
Số tiền cô Trâm thu được từ thửa ruộng là:
0,42 nhân 140.000.000 bằng 58.800.000 đồng
Kết quả là: 58.800.000 đồng.
Ví dụ 4. Một hình chữ nhật có chu vi 54 cm. Nếu tăng chiều rộng thêm 2,5 cm và giảm chiều dài 2,5 cm, ta được một hình vuông. Tính diện tích của hình chữ nhật.
Phân tích để tìm hướng giải quyết.
Bài toán cung cấp chu vi của hình chữ nhật, từ đó có thể xác định tổng chiều dài và chiều rộng.
Khi tăng chiều rộng thêm 2,5 cm và giảm chiều dài 2,5 cm, hai kích thước mới sẽ bằng nhau (vì hình vuông có chiều dài bằng chiều rộng), do đó chiều dài lớn hơn chiều rộng là:
2,5 cộng 2,5 bằng 5 cm.
Bài toán thuộc dạng tìm hai số khi biết tổng và hiệu của chúng.
Giải pháp:
Nửa chu vi của hình chữ nhật là: 54 chia 2 bằng 27 cm
Khi tăng chiều rộng 2,5 cm và giảm chiều dài 2,5 cm, ta có hình vuông. Do đó, chiều dài lớn hơn chiều rộng là:
2,5 cộng 2,5 bằng 5 cm
Chiều dài của hình chữ nhật là:
(27 cộng 5) chia 2 bằng 16 cm
Chiều rộng của hình chữ nhật là:
27 trừ 16 bằng 11 cm
Diện tích của hình chữ nhật ban đầu được tính như sau:
16 nhân 11 bằng 176 cm²
Kết quả là: 176 cm²
3. Bài tập luyện tập dành cho học sinh Toán lớp 5
Bài 1. Một mảnh vườn hình chữ nhật có chiều dài gấp 2 lần chiều rộng. Nếu tăng chiều rộng thêm 2 m và giảm chiều dài 2 m, diện tích mảnh vườn sẽ tăng thêm 12 m². Tính diện tích của mảnh vườn lúc đầu.
Bài 2. Nếu giảm chiều dài của mảnh bìa hình chữ nhật đi 2 cm, ta sẽ có một hình vuông có chu vi 12 cm. Tính diện tích của mảnh bìa hình chữ nhật.
Bài 3. Tam giác ABCD có đáy nhỏ là AB và tổng chiều dài của hai đáy là 44cm. Nếu đáy lớn được kéo dài thêm 10cm thì diện tích hình thang sẽ tăng thêm 60cm2. Xác định diện tích của hình thang ABCD.
Bài 4. Hình thang vuông ABCD (góc A vuông, đáy nhỏ AB) với AB = 6cm và AD = 10cm. Khi thu hẹp hình thang này thành hình chữ nhật mà giữ nguyên đáy nhỏ, diện tích sẽ giảm 40cm2. Tính diện tích hình thang ban đầu.
Bài 5. Hình thang ABCD có đáy nhỏ AB = 1dm, nếu giảm đáy lớn 8cm thì diện tích giảm 64cm2 và còn lại là một hình bình hành. Tìm diện tích của hình thang.
