Bài tập ôn luyện Toán lớp 8 Chương 1 về Hình học với đáp án chi tiết

Buzz

Nội dung bài viết

Bài tập ôn luyện Toán lớp 8 Chương 1 Hình học với các đáp án chi tiết

Xem thêm

Bài tập ôn luyện Toán lớp 8 Chương 1 về Hình học kèm theo đáp án chi tiết. Để tìm hiểu thêm thông tin chi tiết về các bài tập, xin mời quý độc giả tham khảo nội dung bài viết dưới đây.

Bài tập ôn luyện Toán lớp 8 Chương 1 Hình học với các đáp án chi tiết

Bài 1: Một tứ giác sẽ là hình bình hành nếu nó thỏa mãn điều kiện gì?

A. Tứ giác có các góc kề nhau bằng nhau

B. Tứ giác có hai cặp cạnh đối diện song song và bằng nhau

C. Hình thang có hai đường chéo bằng nhau

D. Hình thang có hai đường chéo vuông góc với nhau

Giải thích

+ Đáp án A mô tả hình thang cân

+ Đáp án C là hình thang cân

+ Đáp án D không đủ điều kiện để xác định là hình bình hành

+ Theo đặc điểm nhận diện hình bình hành, một tứ giác là hình bình hành nếu hai cặp cạnh đối diện vừa song song vừa bằng nhau, vì vậy đáp án B là chính xác

Đáp án đúng là: B

Bài 2: Hình bình hành nào có hai đường chéo vuông góc là:

A. Hình chữ nhật

B. Hình thoi

C. Hình vuông

D. Hình thang

Giải thích

Dựa theo đặc điểm nhận diện hình thoi, hình bình hành có hai đường chéo vuông góc chính là hình thoi

Chọn đáp án: B

Bài 3: Tứ giác có hai cặp cạnh đối song song và hai đường chéo bằng nhau là loại hình nào?

A. Hình thang

B. Hình thang cân

C. Hình bình hành

D. Hình thoi

Lời giải

Tứ giác có hai cặp cạnh đối song song là hình thang. Nếu tứ giác còn có hai đường chéo bằng nhau, thì đó là hình thang cân

Đáp án chính xác là: B

Bài 4: Trong các loại tứ giác dưới đây, tứ giác nào có 4 trục đối xứng?

A. Hình chữ nhật

B. Hình vuông

C. Hình bình hành

D. Hình thoi

Giải đáp

+ Hình vuông là tứ giác duy nhất có 4 trục đối xứng

+ Hình chữ nhật có hai trục đối xứng, là các đường trung trực của các cạnh

+ Hình bình hành không có trục đối xứng nào

+ Hình thoi có hai trục đối xứng, chính là hai đường chéo của nó

Chọn đáp án: B

Câu 5:

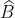
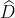
A. 100 độ

B. 105 độ

C. 120 độ

D. 115 độ

Giải đáp

Xem xét tứ giác ABCD, ta có:

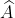
widehat{A} + widehat{B} + widehat{C} + widehat{D}

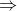
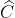
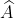
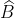
= 360 độ - (70 độ + 120 độ + 50 độ)

= 360 độ - 240 độ = 120 độ

Đáp án chính xác là: C

Bài 6: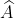

A. 130 độ B. 90 độ C. 110 độ D. 120 độ

Giải pháp

Bài tập ôn luyện Toán lớp 8 Chương 1 Hình học với đáp án chi tiết

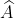
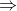
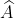
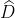
= 180 độ trừ 70 độ

= 110 độ

Lựa chọn đúng là: C

Bài 7: Một tam giác đều với mỗi cạnh dài 14cm. Độ dài của một đường trung bình trong tam giác này là:

A. 34cm

B. 7cm

C. 6,5cm

Dài 21cm

Giải thích:

Chiều dài của một đường trung bình trong tam giác là 14 chia cho 2 bằng 7cm

Lựa chọn đúng là: B

Bài 8: Một hình thang cân có cạnh bên dài 2,5cm và đường trung bình 3cm. Tính chu vi của hình thang.

A. 8cm B. 12cm C. 11,5cm D. 11cm

Giải thích:

Tổng chiều dài của hai đáy là: 3 nhân 2 = 6 cm

Chu vi của hình thang được tính là: 2,5 nhân 2 cộng 6 = 11 cm

Lựa chọn đúng là: D

Bài 9: Đo độ dài của một cạnh hình vuông là 5cm. Độ dài của đường chéo của hình vuông này là bao nhiêu?

A. 25cm

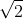
$\sqrt{2}$

C. 10cm D. 5cm

Hướng dẫn giải

Bài tập ôn luyện Toán lớp 8 Chương 1 về Hình học với đáp án chi tiết

Xét hình vuông ABCD với độ dài cạnh là 5cm.

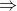
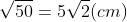
$^{2}$ $^{2}$ $^{2}$ $^{2}$ $^{2}$ $\Rightarrow$ $\sqrt{50} = 5\sqrt{2} (cm)$

Chọn đáp án: B

Bài 10: Một hình thoi có hai đường chéo lần lượt dài 12cm và 16cm. Tính độ dài cạnh của hình thoi đó:

A. 14cm B. 28 cm C. 100 cm D. 10 cm

Hướng dẫn giải

Bài tập ôn tập Toán lớp 8 Chương 1 về Hình học với đáp án chi tiết

Xem xét hình thoi ABCD với hai đường chéo AC = 16cm và BD = 12cm, chúng cắt nhau tại điểm O.

Theo đặc điểm của hình thoi, AC vuông góc với BD, và O là trung điểm của cả hai đường chéo AC và BD

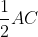
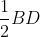
$\frac{1}{2} AC$ $\frac{1}{2} BD$

Áp dụng định lý Pythagoras cho tam giác ABO với góc vuông tại O, ta có:

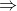
$^{2}$ $^{2}$ $^{2}$ $^{2}$ $^{2}$ $\Rightarrow$

Vì vậy, độ dài cạnh của hình thoi là 10cm

Chọn đáp án: D

Bài 11: Cho hình bình hành ABCD với DC gấp đôi BC. E và F lần lượt là trung điểm của AB và DC. Ký hiệu AF cắt DE tại I, và BF cắt CE tại K.

1. Chọn câu trả lời chính xác nhất.

A. Tứ giác DEBF là một hình bình hành

B. Tứ giác AEFD là một hình thoi

C. Tứ giác EBCF là một hình vuông

D. Cả A và B đều đúng

Giải thích: Xem xét hình bình hành ABCD với E và F lần lượt là trung điểm của AB và CD, và DC gấp đôi BC. Ta có AE = EB = BC = CF = DF = AD; AB // CD và AD // BC

Xem xét tứ giác DEBF, với EB // DF và EB = DF, ta có DEBF là một hình bình hành

Xem xét tứ giác AEFD, với AE = DF và AE // DF, ta có AEFD là hình bình hành. Hơn nữa, vì AE = AD, nên AEFD là hình thoi.

Tương tự, ta cũng có EBCF là hình thoi. Tuy nhiên, EBCF không đủ điều kiện để trở thành hình vuông. Do đó, A và B đúng, C sai.

Chọn đáp án: D

2. Tứ giác EIFK thuộc loại hình gì?

A. Hình chữ nhật B. Hình thoi C. Hình vuông D. Cả A, B, C đều không đúng

Hướng dẫn giải

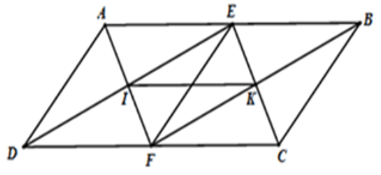
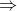
$\Rightarrow$

Dựa vào các thông tin trước đó, ta có tứ giác AEDF và BEFC đều là hình thoi, nên I và K lần lượt là trung điểm của DE và BF.

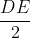
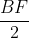
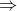
$\frac{DE}{2}$ $\frac{BF}{2}$ $\Rightarrow$

Từ (1) và (2), ta có thể kết luận rằng tứ giác EIFK là hình bình hành.

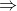
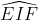
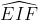
$\Rightarrow$ $\widehat{EIF}$ $\widehat{EIF}$

Chọn đáp án: A

Bài 12: Cho tam giác ABC cân tại A với trung tuyến AM. Gọi I là trung điểm của AC, và K là điểm đối xứng của M qua I.

1. Tứ giác AMCK là loại hình gì?

A. Hình chữ nhật

B. Hình thoi

C. Hình vuông

D. Cả A, B, C đều không đúng

Hướng dẫn giải

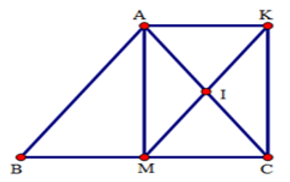
Bài tập ôn tập Toán lớp 8, Chương 1 về Hình học với đáp án chi tiết nhất

Tam giác ABC cân tại đỉnh A với AM là trung tuyến, đồng thời AM cũng là đường cao

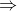
Xem xét tứ giác AMCK với đường chéo AC cắt MK tại điểm I, biết rằng AI = IC và MI = IK (theo giả thiết)

Lựa chọn đúng là: A

2. Tứ giác AKMB thuộc loại hình nào?

Bài tập ôn luyện Toán lớp 8 Chương 1 Hình học với đáp án chi tiết nhất

A. Hình chữ nhật B. Hình thoi C. Hình vuông D. Hình bình hành

$\Rightarrow$

Vì AK = MC (AMCK là hình chữ nhật) và MC = MB (đã cho)

$\Rightarrow$

Đáp án đúng là: D

Bài 13: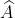 $\widehat{A}$

1. Tứ giác BICD thuộc loại hình nào?

A. Hình chữ nhật B. Hình thoi C. Hình vuông D. Hình bình hành

Giải thích

Bài tập ôn Toán lớp 8 Chương 1 Hình học với đáp án chi tiết nhất

Vì AB // CD (theo giả thiết) nên BI // CD

Thêm vào đó, BI = AB (đã cho) ; AB = CD (đã cho) ⇒ BI = CD

Vì vậy, tứ giác BICD là hình bình hành (1)

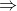
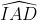
$\Rightarrow$ $\widehat{IAD}$

Xem xét tam giác ADI, BD vừa là trung tuyến vừa là đường cao.

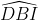
$\widehat{DBI}$

Từ (1) và (2) kết luận rằng BICD là hình chữ nhật (dấu hiệu nhận biết)

Đáp án đúng là: A

2. Đo góc AED là bao nhiêu?

A. 45 độ B. 60 độ C. 90 độ D. 100 độ

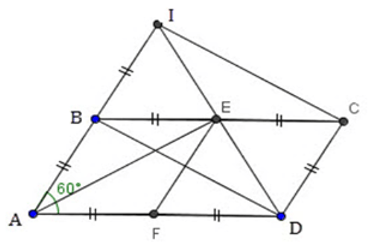
Theo thông tin trước, BICD là hình chữ nhật và E là trung điểm của BC (theo giả thiết), nên E cũng là trung điểm của ID.

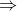
$\perp$ $\Rightarrow$ $\widehat{AED}$

Bài 14: Cho hình vuông ABCD, E là điểm trên cạnh CD. Tia phân giác của góc BAE cắt BC tại M. Hãy chọn câu trả lời đúng.

A. AM = ME

B. AM < ME

C. AM ≤ 2ME

D. AM > 2ME

Giải thích

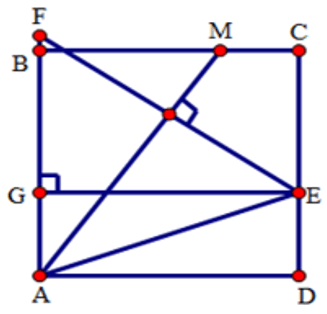
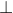
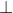
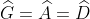
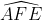
$\perp$ $\perp$ $\widehat{G} = \widehat{A} = \widehat{D}$ $\widehat{FEG} = \widehat{MAB}$ $\widehat{AFE}$

Xem xét tam giác GEF và tam giác BAM có:

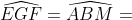
$\widehat{EGF} = \widehat{ABM} =$

GE = AB (= CD);

$\widehat{FEG} = \widehat{MAB}$

Do đó, tam giác ΔGEF bằng tam giác ΔBAM (g.c.g), suy ra EF = AM

Tam giác AEF có AM là đường phân giác đồng thời là đường cao, nên tam giác AEF cân tại đỉnh A

Vì AM là đường trung trực của EF, nên ME = MF

$\Leftrightarrow$ $\Rightarrow$ $\frac{AM}{MB + AM} = \frac{3}{8+3} \Rightarrow \frac{AM}{AB} = \frac{3}{11}$

Nội dung từ Mytour nhằm chăm sóc khách hàng và khuyến khích du lịch, chúng tôi không chịu trách nhiệm và không áp dụng cho mục đích khác.

Nếu bài viết sai sót hoặc không phù hợp, vui lòng liên hệ qua email: [email protected]