1. Quy đồng mẫu các phân số là gì? Phương pháp thực hiện quy đồng mẫu các phân số
- Quy đồng mẫu các phân số là quá trình biến đổi các phân số sao cho chúng có cùng mẫu số mà không làm thay đổi giá trị của chúng. Nói cách khác, quy đồng mẫu số là việc điều chỉnh các phân số với mẫu số khác nhau về cùng một mẫu số chung.
- Để thực hiện việc quy đồng mẫu các phân số, bạn có thể làm theo các bước sau:
- Nhân tử số và mẫu số của phân số đầu tiên với mẫu số của phân số thứ hai.
- Nhân tử số và mẫu số của phân số thứ hai với mẫu số của phân số đầu tiên.
- Nếu mẫu số của phân số thứ hai chia hết cho mẫu số của phân số thứ nhất, bạn có thể quy đồng mẫu số theo các bước sau:
- Chọn mẫu số chung là mẫu số của phân số thứ hai.
- Tính thừa số phụ bằng cách chia mẫu số thứ hai cho mẫu số thứ nhất.
- Nhân cả tử số và mẫu số của phân số đầu tiên với thừa số phụ đã tính.
- Giữ nguyên phân số thứ hai.
- Lưu ý: Để quy đồng mẫu số một cách nhanh chóng, bạn nên chọn mẫu số chung (MSC) là số nhỏ nhất có thể. Cách làm này giúp việc tính toán dễ dàng hơn và giảm thiểu lỗi. Các bước thực hiện như sau:
- Chọn mẫu số lớn nhất trong các mẫu số cần quy đồng.
- Kiểm tra xem mẫu số lớn nhất có chia hết cho các mẫu số còn lại không.
- Nhân mẫu số lớn nhất với các số 2, 3, 4… cho đến khi tìm được số chia hết cho tất cả các mẫu số còn lại. Chọn số đó làm MSC.
2. Bài tập Quy đồng mẫu số các phân số lớp 4 (kèm giải đáp chi tiết)
Bài 1: Tìm mẫu số chung nhỏ nhất của hai phân số 3/4 và 1/5.
Giải: Ta có
- Số 10 chia hết cho 5 nhưng không chia hết cho 4, vì vậy 10 không phải là mẫu số chung của hai phân số.
- Số 20 chia hết cho cả 4 và 5, do đó 20 là mẫu số chung nhỏ nhất của hai phân số.
- Số 32 chia hết cho 4 nhưng không chia hết cho 5, vì vậy 32 không phải là mẫu số chung của hai phân số.
- Số 60 chia hết cho cả 4 và 5, nên 60 là mẫu số chung của hai phân số.
Ta nhận thấy 20 là số nhỏ nhất chia hết cho cả 4 và 5.
Vậy, mẫu số chung nhỏ nhất của hai phân số đã cho là 20.
Bài 2: Quy đồng mẫu số của các phân số 2/3 và 1/4, ta sẽ có phân số 8/12 và phân số...
Giải:
- Chọn mẫu số chung (MSC) là 12
- Quy đồng mẫu số các phân số 2/3 và 1/4, ta có:
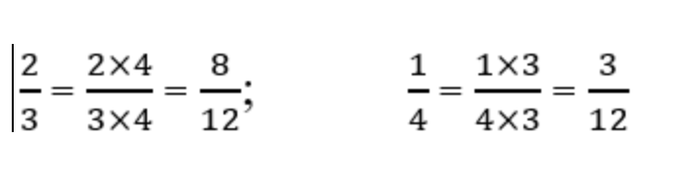
Vậy khi quy đồng mẫu số của các phân số 2/3 và 1/4, ta nhận được hai phân số 8/12 và 3/12.
Bài 3: Quy đồng mẫu số của ba phân số 3/5, 2/3 và 8/9. Các phân số này sẽ có giá trị như thế nào sau khi quy đồng?
Giải đáp:
Chúng ta thấy rằng 45 chia hết cho 5, 3 và 9. Do đó, mẫu số chung nhỏ nhất là 45.
Sau khi quy đồng mẫu số, các phân số sẽ là:
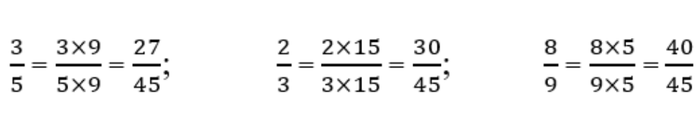
Vậy khi quy đồng mẫu số của ba phân số 3/5, 2/3 và 8/9, chúng ta sẽ có các phân số tương ứng là 27/45, 30/45 và 40/45.
Bài 4: Chuyển các phân số 63/72 và 45/135 thành hai phân số có cùng mẫu số là 24.
Do đó, các phân số sau khi quy đồng sẽ là:
Giải:
Khi rút gọn các phân số 63/72 và 45/135, ta có:
63/72 = 7/8
45/135 = (45 chia 5) / (135 chia 5) = 9/27 = 1/3.
Khi quy đồng mẫu số hai phân số 7/8 và 1/3 với mẫu số chung là 24, ta có:

Vậy các phân số 63/72 và 45/135 sau khi quy đồng sẽ được viết thành hai phân số có mẫu số 24 là 21/24 và 8/24.
Bài 5: Xác định hai phân số tương ứng với 5/8 và 7/12 khi có mẫu số chung là 24.
Giải:
Chọn mẫu số chung (MSC) là 24.
Khi quy đồng mẫu số hai phân số 5/8 và 7/12 với mẫu số chung là 24, ta có:
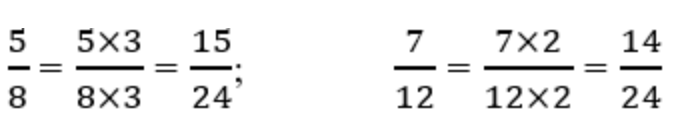
Vậy hai phân số tương ứng với 5/8 và 7/12 khi quy đồng với mẫu số chung 24 là 15/24 và 14/24.
Bài 6: Tìm mẫu số chung nhỏ nhất của hai phân số 5/6 và 7/18.
Giải:
Ta nhận thấy rằng 18, 36 và 54 đều chia hết cho cả 6 và 18.
Số 18 là mẫu số chung nhỏ nhất chia hết cho mẫu số của hai phân số 5/6 và 7/18.
Vậy mẫu số chung nhỏ nhất của hai phân số là 18.
Bài 7: Quy đồng mẫu số ba phân số 1/3, 3/4 và 7/12. Các phân số sau khi quy đồng sẽ là gì?
Giải:
Chúng ta thấy rằng 12 chia 3 được 4 và 12 chia 4 được 3, vì vậy mẫu số chung nhỏ nhất là 12.
Khi quy đồng mẫu số các phân số, ta có: 1/3 = 4/12
3/4 tương đương với 9/12.
Phân số 7/12 giữ nguyên.
Vậy khi quy đồng mẫu số ba phân số 1/3, 3/4 và 7/12, ta có các phân số lần lượt là 4/12, 9/12 và 7/12.
Bài 8: Thực hiện quy đồng mẫu số cho các phân số sau đây:
1/6 và 4/5
11/49 và 8/7;
12/5 và 5/9
Trả lời:
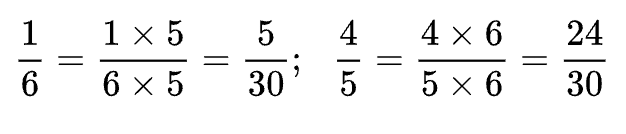
Khi quy đồng mẫu số hai phân số 1/6 và 4/5, ta có các phân số 5/30 và 24/30.
+) Giữ nguyên phân số 11/49; 8/7 được quy đổi thành 56/49
Do đó, khi quy đồng mẫu hai phân số 11/49 và 8/7, ta có hai phân số là 11/49 và 56/49.
3. Các phương pháp học hiệu quả môn Toán lớp 4
Để đạt kết quả cao trong môn Toán lớp 4 cũng như các môn học khác, các bạn học sinh cần áp dụng phương pháp học hiệu quả. Dưới đây là một số cách học mà các bạn có thể tham khảo để cải thiện hiệu quả học tập của mình:
- Ghi nhớ lý thuyết là bước quan trọng và cần thiết. Việc ghi nhớ không chỉ đơn thuần là học thuộc lòng công thức, mà cần phải hiểu rõ các ký hiệu, công thức, và quy trình thực hiện. Đây là cách giúp học sinh nắm vững kiến thức cơ bản, tránh việc bỏ sót những kiến thức quan trọng và hiểu sâu bản chất của các vấn đề toán học.
- Ghi nhớ các phương pháp giải cho từng dạng bài tập là rất quan trọng, mặc dù lớp 4 chưa có quá nhiều dạng bài nhưng các dạng toán cơ bản cần phải được nắm vững. Mỗi dạng bài đều có phương pháp giải riêng biệt, như quy đồng mẫu số, tìm hai số khi biết tổng hay hiệu, tính trung bình cộng, toán chia hết, toán về hình học hay toán có lời văn,...
- Học cách tóm tắt và phân tích kỹ nội dung đề bài để tìm ra phương pháp giải phù hợp nhất. Không phải bài nào cũng cần tóm tắt, nhưng việc đọc hiểu và phân tích đề bài là rất quan trọng để nhận diện dạng bài và phương pháp giải hiệu quả.
- Thực hành sau khi đã nắm vững lý thuyết là cần thiết. Làm nhiều bài tập sẽ giúp học sinh phản xạ nhanh hơn, cải thiện kỹ năng tính toán và bổ sung kiến thức. Khi làm quen với các dạng bài tập, học sinh sẽ không còn bỡ ngỡ mà sẽ dễ dàng xử lý bài toán.
- Phát triển tính tự giác là rất quan trọng trong học tập. Dù có sự hỗ trợ từ giáo viên hay phụ huynh, nếu học sinh không có ý thức tự học thì kết quả học tập sẽ không cải thiện. Môn toán yêu cầu sự tập trung cao để hiểu và giải quyết các bài toán một cách hiệu quả.
- Học từ những sai lầm là rất cần thiết. Sự thất bại trong bài tập không nên khiến học sinh chán nản hay sợ hãi. Thay vào đó, việc nhận ra và học hỏi từ những lỗi sai sẽ giúp cải thiện kỹ năng và bổ sung kiến thức còn thiếu.
