1. Bài tập Toán lớp 5, bài 173: Ôn tập tổng hợp
Phần 1
Chọn đáp án đúng bằng cách khoanh tròn vào lựa chọn phù hợp:
Bài 1. 0,3 =
A. 3/10
B. 3/100
C. 3/1000
D. 3/10000
Phương pháp: Chuyển đổi 0,3% thành phân số thập phân dựa trên nguyên tắc 1% = 1/100.
Cách giải:
Ta có: 0,3% = 0,3/100 = 3/1000.
Lựa chọn C.
Bài 2: Để tính 60% của 45, ta thực hiện như sau:
A. Nhân 45 với 60.
B. Chia 45 cho 60.
C. Nhân 45 với 100 rồi chia kết quả cho 60.
D. Nhân 45 với 60 rồi chia kết quả cho 100.
Phương pháp:
Để tính 60% của 45, ta có thể chia 45 cho 100 và nhân với 60, hoặc nhân 45 với 60 và chia cho 100.
Cách giải:
Để tính 60% của 45, ta có thể chia 45 cho 100 và nhân với 60, hoặc nhân 45 với 60 và chia cho 100.
Trong các phương pháp tính trên, phương pháp chính xác là 'Nhân 45 với 60 rồi chia cho 100'.
Chọn D.
Bài 3. Trong số các hình dưới đây, hình nào có chiều cao gấp đôi chiều cao của hình H?
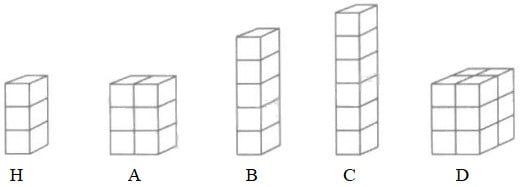
Phương pháp:
Kiểm tra chiều cao của từng hình và so sánh với chiều cao của hình H.
Cách giải:
Xem xét các hình vẽ, ta có:
- Hình H có chiều cao gấp 2 lần cạnh của hình lập phương nhỏ.
- Hình A có chiều cao gấp 3 lần cạnh của hình lập phương nhỏ.
- Hình B có chiều cao gấp 5 lần cạnh của hình lập phương nhỏ.
- Hình C có chiều cao gấp 6 lần cạnh của hình lập phương nhỏ.
- Hình D có chiều cao gấp 3 lần cạnh của hình lập phương nhỏ.
Trong số các hình đã cho, hình C cao gấp đôi hình H.
Hãy chọn hình C.
Phần 2
Bài 1. Một tấm bìa hình vuông đã được tô đậm như trong hình vẽ. Tính diện tích của phần tô đậm.
Phương pháp:
- Khi ghép 4 phần chưa được tô, ta sẽ tạo ra một hình tròn có bán kính 10cm.
- Tính diện tích của hình tròn bán kính 10cm bằng công thức S = r × r × 3,14.
- Diện tích tấm bìa hình vuông = cạnh × cạnh.
- Diện tích phần tô đậm = diện tích tấm bìa hình vuông - diện tích hình tròn bán kính 10cm.
Hướng dẫn giải:
Ghép 4 phần chưa tô đậm sẽ tạo thành một hình tròn có bán kính 10cm.
Diện tích của hình tròn bán kính 10cm (hay diện tích phần không tô) được tính như sau:
10 ⨯ 10 ⨯ 3,14 = 314 (cm2)
Độ dài cạnh của tấm bìa hình vuông được tính như sau:
10 + 10 = 20 (cm)
Diện tích của tấm bìa hình vuông được tính như sau:
20 ⨯ 20 = 400 (cm2). Do đó, diện tích phần đã tô đậm là:
400 - 314 = 86 (cm2)
Kết quả là: 86 cm2.
Bài 2. Mẹ chi 96.000 đồng để mua thịt lợn và rau quả. Số tiền mua thịt lợn bằng 140% số tiền mua rau quả. Hãy tính số tiền mẹ chi cho rau quả.
Phương pháp:
Giả sử số tiền mua rau quả là 100%, thì số tiền mua thịt lợn là 140%, và tổng số tiền chi cho thịt và rau quả là 100% + 140% = 240% so với số tiền rau quả.
Để tính số tiền mua rau quả, chia tổng số tiền chi cho thịt và rau quả cho 240, sau đó nhân với 100.
Cách giải:
Giả sử số tiền mua rau quả là 100%, thì số tiền mua thịt lợn là 140%.
96.000 đồng tương ứng với tổng số phần trăm là
100% + 140% = 240%
Số tiền mẹ đã chi cho rau quả là:
96.000 : 240 ⨯ 100 = 40.000 (đồng)
Kết quả: 40.000 đồng.
2. Bài toán trí tuệ lớp 5
Bài toán trí tuệ lớp 5 - Dạng toán số học
Số học trong môn toán trí tuệ lớp 5 thường là dạng bài văn cần suy luận. Phụ huynh có thể tham khảo đáp án và câu hỏi để kiểm tra xem con em mình làm đúng không nhé!
Dạng bài tập toán phát triển trí thông minh lớp 5 có phần khó và yêu cầu sự kết hợp giữa tư duy và kiến thức xã hội. Những câu đố và câu hỏi trong dạng bài này thường liên kết với nhau theo chủ đề. Nếu trẻ giải được câu đầu, sẽ giúp tìm ra đáp án cho câu tiếp theo…
Bài tập 1
Trong một lớp học có 30 học sinh, trong đó có 10 học sinh giỏi môn văn và 22 học sinh giỏi môn toán. Hãy chứng minh rằng ít nhất có 1 học sinh xuất sắc ở cả hai môn văn và toán.
Bài tập 2
Trong lớp học, tất cả học sinh đều tham gia học bơi và học võ. Có 12 học sinh học bơi, 8 học sinh học võ, và 5 học sinh không tham gia cả hai lớp. Hãy tính số học sinh đang học cả bơi và võ.
Bài tập 3
Lớp toán có 20 học sinh. Trong đó, 10 học sinh yêu thích ăn lê và 15 học sinh yêu thích ăn táo.
a. Tính số học sinh thích cả táo và lê.
b. Có thể xác định số học sinh không thích táo cũng như không thích lê không?
c. Nếu mỗi học sinh đều thích ít nhất một loại quả, lê hoặc táo, thì có bao nhiêu học sinh thích cả hai loại quả này?
Toán phát triển trí thông minh Lớp 5 – Dạng hình học tư duy
Học sinh lớp 5 đã được tiếp xúc với hình học, một môn học giúp phát triển tư duy toán học và trí tưởng tượng. Để cải thiện khả năng hiểu bài và luyện tập hiệu quả, phụ huynh nên cho trẻ luyện giải các bài toán hình học.
Các bài tập thường là ghép các hình lại để tạo thành bức tranh hoàn chỉnh, đếm số hình nhỏ bên trong, hoặc điều chỉnh các cạnh để tạo hình dạng mong muốn. Học sinh lớp 5 cũng sẽ gặp một số bài toán về các hình không gian đơn giản, giúp phát triển trí tưởng tượng và tư duy toán học.
Bài tập 1
Dựa vào hình ảnh dưới đây, chọn và đưa ra câu trả lời đúng nhất:
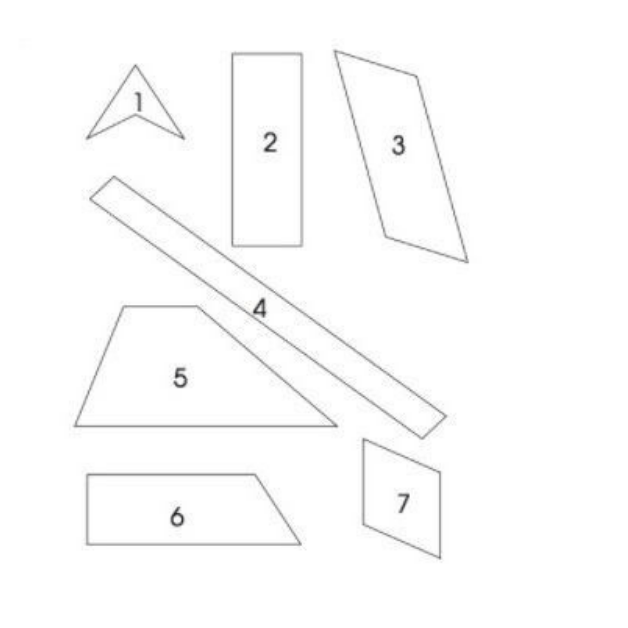
1. Hình vuông thuộc dạng số mấy?
2. Hình thoi thuộc dạng số mấy?
3. Hình chữ nhật thuộc dạng số mấy?
4. Hình thang thuộc dạng số mấy?
Toán phát triển trí thông minh lớp 5 – Dạng bài toán tổ hợp nâng cao
Các bài toán tổ hợp thường khó hơn và yêu cầu trẻ kết hợp tư duy, logic và trí tưởng tượng. Học sinh lớp 5 thường phải tìm nhiều đáp án khác nhau và có thể gặp khó khăn trong việc không bỏ sót dữ liệu hoặc thiếu tư duy sáng tạo.
Toán tổ hợp lớp 5 giúp phát triển tư duy qua việc phân tích vấn đề từ nhiều góc độ và kết hợp chúng để tìm điểm chung. Khi tìm được điểm chung, trẻ sẽ dễ dàng có câu trả lời chính xác hơn.
Bài tập 1. Từ nhà bạn đến thành phố A có 3 con đường. Từ thành phố A đến thành phố C có 2 con đường. Hỏi tổng số con đường từ nhà bạn đến thành phố C là bao nhiêu?
Bài tập 2. Từ thành phố A đến tòa nhà F có 4 con đường khác nhau: B, C, D, E. Hãy tính số con đường từ A đến F, với điều kiện tất cả các con đường đều cùng một chiều.
Bài tập 3. Hoa có 3 loại cốc và 2 loại thìa khác nhau. Hỏi Hoa có thể tạo ra bao nhiêu bộ cốc và thìa khác nhau, mỗi bộ gồm 1 cốc và 1 thìa.
3. Các bài toán giải bằng phương pháp tính ngược từ kết quả - Toán nâng cao lớp 5
Ví dụ 1: Một người bán gạo. Lần đầu tiên, người đó bán 1/3 số gạo mang theo. Lần thứ hai, bán 3/5 số gạo còn lại. Cuối cùng, người đó bán nốt 24 kg là hết số gạo. Hỏi:
a. Số gạo người đó mang theo ban đầu là bao nhiêu kg?
b. Trong hai lần bán đầu, mỗi lần người đó bán bao nhiêu kg gạo?
Giải
a) Lần bán gạo cuối cùng là 24 kg, tương ứng với:
1 − 3/5 = 2/5 (phần gạo còn lại sau lần bán đầu tiên)
Số gạo còn lại sau lần bán đầu tiên là
24 ÷ 2/5 = 60 (kg)
Số gạo 60 kg này tương ứng với:
1 − 1/3 = 2/3 (lượng gạo ban đầu)
Lượng gạo ban đầu là
60 ÷ 2/3 = 90 (kg)
b) Số kg gạo bán được trong lần đầu là
1/3 × 90 = 30 (kg)
Lần bán thứ hai người đó đã bán được
3/5 × (90 − 30) = 36 (kg)
Kết quả: a) 90 kg
b) Lần đầu: 30 kg, lần sau: 36 kg
Ví dụ 2: An, Bình, và Chi có tổng cộng 108 con tem. Sau khi An tặng Bình 10 con tem, Bình tặng Chi 8 con tem, và Chi tặng lại An 6 con tem, số tem của ba người này trở nên bằng nhau. Tính số tem mỗi người có lúc đầu.
Giải pháp
Sau khi trao đổi, số tem của mỗi người là:
108 ÷ 3 = 36 (con tem)
Số tem ban đầu của An là
36 + 10 – 6 = 40 (con tem)
Số tem ban đầu của Bình là
36 – 10 + 8 = 34 (con tem)
Số tem ban đầu của Chi là
36 – 8 + 6 = 38 (con tem)
Kết quả: An có 40 con tem
Bình có 34 con tem
Chi sở hữu 38 con tem
