Bài tập Toán lớp 5 trang 115: Hướng dẫn chi tiết về thể tích hình học

1. Giải bài toán lớp 5 trang 115: Xác định thể tích của các hình

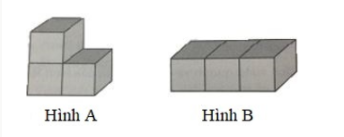
Bài 1: Hãy xem xét các hình dưới đây:

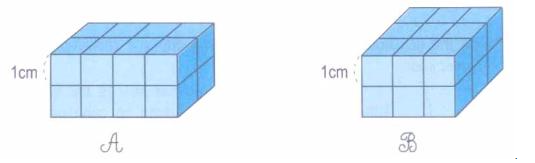
Hướng dẫn giải: Quan sát các hình vẽ để đếm số lượng khối lập phương nhỏ trong mỗi hình. Hình có nhiều khối lập phương nhỏ hơn sẽ có thể tích lớn hơn.

Giải đáp

Bài 2: Hình hộp chữ nhật A chứa bao nhiêu khối lập phương nhỏ? Hình hộp chữ nhật B chứa bao nhiêu khối lập phương nhỏ? Hình nào có thể tích lớn hơn?

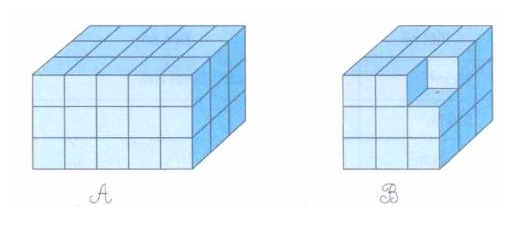
Cách giải: Quan sát các hình vẽ để tính số khối lập phương nhỏ trong hình A và hình B. Hình nào có nhiều khối lập phương nhỏ hơn thì có thể tích lớn hơn.

Giải đáp: 

- Hình A có chiều dài 5 ô vuông, chiều rộng 3 ô vuông và chiều cao 3 ô vuông.

+ Hình A chứa 5 × 3 × 3 = 45 khối lập phương nhỏ.

- Hình B có các cạnh đều dài 3 ô vuông nhưng thiếu một ô vuông.

+ Hình B có 3 × 3 × 3 – 1 = 26 khối lập phương nhỏ.

Vì 45 > 26.

Do đó, thể tích của hình A lớn hơn thể tích của hình B, hoặc thể tích hình B nhỏ hơn thể tích hình A.

Bài 3: Có 6 khối lập phương nhỏ, mỗi khối có cạnh 1 cm. Hãy xếp chúng thành một hình hộp chữ nhật. Có bao nhiêu cách sắp xếp khác nhau?

Cách giải: Sử dụng công thức tính thể tích để xếp các khối thành hình hộp chữ nhật.

Giải đáp:

Vì 6 = 1 × 6 = 2 × 3.

Vậy có thể xếp thành hình hộp chữ nhật theo các cách sau:

Có tổng cộng 6 cách xếp như sau:

Cách 1: Chiều dài 1 ô vuông, chiều rộng 1 ô vuông, chiều cao 6 ô vuông.

Cách 2: Chiều dài 6 ô vuông, chiều rộng 1 ô vuông, chiều cao 1 ô vuông.

Cách 3: Chiều dài 3 ô vuông, chiều rộng 1 ô vuông, chiều cao 2 ô vuông.

Cách 4: Chiều dài 2 ô vuông, chiều rộng 1 ô vuông, chiều cao 3 ô vuông.

Cách 5: Chiều dài 3 ô vuông, chiều rộng 2 ô vuông, chiều cao 1 ô vuông.

Cách 6: Chiều dài 2 ô vuông, chiều rộng 3 ô vuông, chiều cao 1 ô vuông.

2. Lý thuyết về thể tích của hình học

Thông tin cần lưu ý: Thể tích của một hình là không gian mà hình đó chiếm giữ.

2.1 Thể tích của hình hộp chữ nhật

Ví dụ: Một bể nước hình hộp chữ nhật A có thể tích là lượng không khí mà hình A có thể chứa. Nếu đổ nước vào bể, thể tích của nước sẽ nhỏ hơn thể tích của bể.

Nguyên tắc: Để tính thể tích của hình hộp chữ nhật, bạn cần nhân chiều dài với chiều rộng và sau đó nhân kết quả với chiều cao (cùng đơn vị đo).

Chú ý: Diện tích đáy của hình hộp chữ nhật chính là tích của chiều dài và chiều rộng. Do đó, để tính thể tích, bạn chỉ cần nhân diện tích đáy với chiều cao.

Ví dụ: Tính thể tích của một hình hộp chữ nhật với chiều dài 12cm, chiều rộng 5cm và chiều cao 8cm.

Phương pháp: Ba kích thước của hình hộp chữ nhật đã có cùng đơn vị đo, vì vậy để tính thể tích, bạn chỉ cần nhân chiều dài với chiều rộng và sau đó nhân với chiều cao.

Kết quả:

Thể tích của hình hộp chữ nhật là:

12 x 5 x 8 = 480 cm³

Kết quả: 480 cm³.

2.3 Thể tích của hình lập phương

Nguyên tắc: Để tính thể tích hình lập phương, bạn nhân cạnh với chính nó ba lần.

Ví dụ: Tính thể tích của hình lập phương với cạnh dài 2cm.

Kết quả:

Thể tích của hình lập phương là:

2×2×2=8 (cm³)
 

Kết quả cuối cùng: 8 cm³

2.3 Các loại bài toán tính thể tích của hình

Dạng 1: Tính thể tích của hình khi đã biết độ dài cạnh

Cách thực hiện: Sử dụng công thức tính thể tích phù hợp với hình đã cho.

Dạng 2: Tính thể tích của hình khi biết diện tích xung quanh hoặc diện tích toàn phần

Cách thực hiện: Từ diện tích xung quanh hoặc diện tích toàn phần, tính ra độ dài của một cạnh, sau đó tính thể tích dựa trên kết quả này.

Dạng 3: So sánh thể tích của hai hình khác nhau

Phương pháp: Tính thể tích từng hình theo công thức, sau đó so sánh kết quả.

Dạng 4: Bài toán có lời văn

Phương pháp: Đọc kỹ đề bài, xác định loại toán và yêu cầu, rồi giải bài toán dựa trên thông tin đó.

3. Các bài tập ứng dụng về thể tích của hình

3.1 Đề bài

I. Trắc nghiệm

Câu 1: Chọn dấu thích hợp để hoàn thành câu: 895 dm³ … 1m³

A: >

B: <

C: =

D: Không thể so sánh

Câu 2: So sánh thể tích của hai hình C và D.

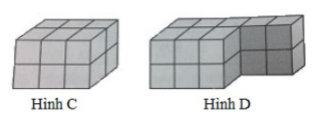
A. Thể tích của hình C lớn hơn

B. Thể tích của hình D lớn hơn

C. Thể tích của hai hình là bằng nhau

D. Không thể so sánh

Câu 3: Xác định số lượng hình lập phương nhỏ trong hình dưới đây.

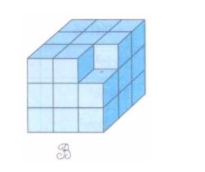
A. 25

B. 27

C. 26

D. 28

Câu 4: Trong hình dưới đây có bao nhiêu hình lập phương nhỏ?

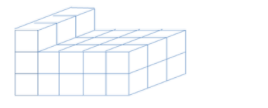
A. 30

B. 31

C. 32

D. 33

Câu 5: Hình nào có thể tích lớn hơn?

A. Hình C

B. Hình D

C. Thể tích của hai hình là như nhau

D. Không có cơ sở so sánh

Câu 6: Một khối đá hình hộp chữ nhật với kích thước dài 1m, rộng 0,8m, cao 0,9m. Tính khối lượng của khối đá nếu 1m³ đá nặng 550kg?

A. 396 kg

B. 369 g

C. 369 kg

D. 496 kg

Câu 7: Một bể bơi hình lập phương có cạnh 8m. Hãy tính số lít nước cần để làm đầy bể?

A. 512 lít

B. 5120 lít

C. 51200 lít

D. 512000

Câu 8: Một bể nước hình chữ nhật có chiều dài 3m, rộng 2m và cao 1,5m. Nếu bể chứa nước với thể tích bằng 2/3 thể tích toàn bộ bể, vậy bể chứa bao nhiêu lít nước?

A. 6000

B. 5000

C. 4000

D. 3000

Câu 9: Tính thể tích của hình hộp chữ nhật có các kích thước lần lượt là: 15m, 3,2m và 4,5m.

Thể tích của hình hộp chữ nhật này là:

A. 206 m³

B. 216 m³

C. 226 m³

D. 236 m³

Câu 10: Một vòi nước có khả năng xả 800 lít nước mỗi giờ. Vậy, để làm đầy một bể nước hình chữ nhật với các kích thước 3m dài, 1,5m rộng và 1,6m cao, thì vòi nước cần bao nhiêu thời gian?

A. 6 giờ

B. 7 giờ

C. 8 giờ

D. 9 giờ

II. Bài tập tự luận

Câu 1: Tính thể tích của hình hộp chữ nhật khi diện tích xung quanh là 10000 cm², chiều cao là 50 cm và chiều dài lớn hơn chiều rộng 12 cm.

Câu 2: Xác định thể tích của hình hộp chữ nhật với chu vi đáy là 140 m, chiều rộng bằng 3/4 chiều dài và chiều cao là trung bình cộng của chiều rộng và chiều dài.

Câu 3: Một hình hộp chữ nhật có chiều rộng 6 dm, chiều dài gấp đôi chiều rộng, và chiều cao là trung bình cộng của chiều dài và chiều rộng. Hỏi có thể xếp được bao nhiêu hình lập phương có thể tích 1 cm³ để đầy hình hộp chữ nhật đó?

Câu 4: Người ta dự định xây một phòng hình hộp chữ nhật cho 500 người. Phòng có chiều dài 25 m và chiều rộng 15 m. Vậy, phòng cần cao bao nhiêu mét nếu mỗi người cần 3 m³ không khí?

Câu 5: Một thùng sắt hình hộp chữ nhật hiện đang đầy nước. Thùng có chiều dài 25 cm, chiều rộng bằng 3/5 chiều dài và chiều cao là trung bình cộng của chiều dài và chiều rộng. Hỏi thùng đó đang chứa bao nhiêu lít nước? (1 dm³ = 1 lít)

3.2 Đáp án

I. Câu hỏi trắc nghiệm

Câu 1: B

Câu 2: B

Câu 3: C

Câu 4: D

Câu 5: C

Câu 6: A

Câu 7: D

Câu 8: A

Câu 9: B

Câu 10: D

II. Phần tự luận

Câu 1:

Chu vi của đáy là:

10000 : 50 = 200 (cm)

Nửa chu vi của đáy là:

200 chia 2 = 100 (cm)

Chiều dài của hình hộp chữ nhật là:

(100 cộng 12) chia 2 = 56 (cm)

Chiều rộng của hình hộp chữ nhật là:

100 trừ 56 = 44 (cm)

Thể tích của khối hộp chữ nhật là:

56 x 44 x 50 = 123200 (cm³)

Kết quả: 123200 cm³

Câu 2:

Nửa chu vi của đáy là:

140 chia 2 = 70 (m)

Số phần bằng nhau là:

3 cộng 4 = 7 (phần)

Chiều rộng của khối hộp chữ nhật là:

70 chia 7 nhân 3 = 30 (m)

Chiều dài của khối hộp chữ nhật là:

70 trừ 30 = 40 (m)

Chiều cao của khối hộp chữ nhật là:

(30 cộng 40) chia 2 = 35 (m)

Thể tích của khối hộp chữ nhật là:

30 nhân 40 nhân 35 = 42000 (m³)

Kết quả: 42000 m³

Câu 3:

Chuyển đổi 1 cm³ = 0,001 dm³

Chiều dài của khối hộp chữ nhật là:

6 nhân 2 bằng 12 (dm)

Chiều cao của hình hộp chữ nhật là:

(6 cộng 12) chia 2 bằng 9 (dm)

Thể tích của hình chữ nhật là:

6 nhân 12 nhân 9 bằng 648 (dm³)

Số khối lập phương có thể đặt vừa trong hình hộp chữ nhật là:

648 chia 0,001 bằng 648000 (khối)

Kết quả: 648000 khối

Câu 4:

Thể tích cần thiết để chứa đủ 500 người là:

500 nhân 3 bằng 1500 (m³)

Chiều cao của căn phòng là:

1500 chia 25 chia 15 bằng 4 (m)

Kết quả: 4m

Câu 5:

Chiều rộng của thùng sắt là:

25 nhân 3 chia 5 bằng 15 (cm)

Tổng chiều dài và chiều rộng là:

25 cộng 15 bằng 40 (cm)

Chiều cao của thùng sắt là:

40 chia 2 bằng 20 (cm)

Thể tích của thùng sắt là:

15 nhân 25 nhân 20 bằng 7500 (cm³)

7500 cm³ chuyển đổi thành 7,5 dm³ tương đương 7,5 lít

Thùng hiện chứa 7,5 lít nước

Kết quả: 7,5 lít nước