Bài tập Toán lớp 6 - Chủ đề quy đồng mẫu số với đáp án chi tiết

Buzz

Nội dung bài viết

A. Kiến thức cơ bản

1. Định nghĩa

2. Quy tắc quy đồng mẫu số

B. Bài tập ứng dụng

Xem thêm

Chúng tôi xin giới thiệu bài viết về 'Bài tập Toán lớp 6 - Chủ đề quy đồng mẫu số với đáp án chi tiết', hy vọng nội dung này sẽ cung cấp thông tin bổ ích cho bạn đọc.

A. Kiến thức cơ bản

1. Định nghĩa

Quy đồng mẫu số cho nhiều phân số là quá trình chuyển đổi các phân số đó thành những phân số tương đương nhưng có chung một mẫu số.

2. Quy tắc quy đồng mẫu số

Dạng 1: Quy đồng mẫu cho các phân số.

Để quy đồng mẫu số cho nhiều phân số, thực hiện các bước sau:

Phương pháp 1:

+ Bước 1. Xác định một bội chung của các mẫu số (thường là BCNN) để sử dụng làm mẫu số chung.

Để tìm bội chung nhỏ nhất của hai hay nhiều số, thường thực hiện theo các bước sau:

Bước đầu tiên là phân tích các số đã cho thành các thừa số nguyên tố

Tiếp theo, chọn các thừa số nguyên tố chung và riêng

Với mỗi thừa số nguyên tố, chọn số mũ lớn nhất của nó

Tính tích của các thừa số đã chọn với số mũ lớn nhất, kết quả là bội chung nhỏ nhất cần tìm.

+ Bước 2. Tìm thừa số phụ cho từng mẫu bằng cách chia mẫu chung cho mỗi mẫu số.

+ Bước 3. Nhân cả tử số và mẫu số của mỗi phân số với thừa số phụ tương ứng.

Lưu ý: Trước khi thực hiện quy đồng, hãy đảm bảo phân số có mẫu dương và rút gọn các phân số nếu cần.

Phương pháp 2:

- Để quy đồng mẫu số cho hai phân số, có thể thực hiện theo cách sau:

+ Nhân cả tử số và mẫu số của phân số đầu tiên với mẫu số của phân số thứ hai.

+ Nhân cả tử số và mẫu số của phân số thứ hai với mẫu số của phân số đầu tiên.

- Nếu mẫu số của phân số thứ hai chia hết cho mẫu số của phân số đầu tiên, có thể quy đồng mẫu số của hai phân số theo cách sau:

+ Chọn mẫu số chung là mẫu số của phân số thứ hai.

+ Tìm thừa số phụ bằng cách chia mẫu số của phân số thứ hai cho mẫu số của phân số thứ nhất.

+ Nhân cả tử số và mẫu số của phân số đầu tiên với thừa số phụ tương ứng.

+ Giữ nguyên phân số thứ hai

Lưu ý: Mẫu số chung thường được chọn là số tự nhiên nhỏ nhất khác 0 mà chia hết cho tất cả các mẫu số.

Dạng 2: Bài toán quy đồng mẫu số cho các phân số.

Để xác định hai phân số có bằng nhau không, cần đưa chúng về cùng một mẫu số. Nếu tử số và mẫu số của hai phân số giống nhau thì chúng bằng nhau.

Có hai phương pháp để đưa hai phân số về cùng một mẫu số:

+ Phương pháp 1. Rút gọn phân số.

+ Phương pháp 2. Quy đồng mẫu số.

Để tìm giá trị của x trong phương trình phân số, có thể quy đồng mẫu số trước rồi giải x sao cho các tử số bằng nhau.

B. Bài tập ứng dụng

Ví dụ: Quy đồng mẫu số cho các phân số 1/3 và 1/2.

Hướng dẫn giải:

Tính BCNN của 3 và 2 là 6. Vì vậy, mẫu số chung của hai phân số là 6.

Thừa số phụ của 3 đối với 6 là 2: 6 / 3 = 2.

Thừa số phụ của 2 đối với 6 là 3: 6 / 2 = 3.

Bài 1:

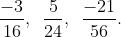
$\frac{-3}{16},\,\,\,\frac{5}{24},\,\,\,\frac{-21}{56}.$

b) Trong các phân số đã cho, phân số nào chưa được rút gọn?

Dựa trên nhận xét đó, chúng ta có thể quy đồng các phân số này bằng cách nào?

Hướng dẫn:

Chuyển các phân số đã cho thành các phân số tương đương với cùng một mẫu số chung.

Hướng dẫn giải:

a) Tính BCNN của 16, 24 và 56 là 336 ➝ Mẫu số chung của các phân số là 336.

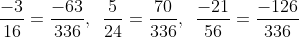
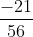
$\frac{-3}{16} = \frac{-63}{336},\,\,\,\frac{5}{24} = \frac{70}{336},\,\,\,\frac{-21}{56} = \frac{-126}{336}$ $\frac{-21}{56}$ $\frac{-9}{48},\,\,\,\frac{10}{48},\,\,\,\frac{-18}{48}$

Bài 2:

Đưa các phân số sau về cùng một mẫu số:

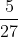
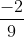
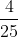
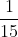
$\frac{3}{8}$ $\frac{5}{27}$ $\frac{-2}{9}$ $\frac{4}{25}$ $\frac{1}{15}$

Hướng dẫn:

Chuyển các phân số đã cho thành các phân số tương đương với cùng một mẫu số chung.

Lời giải:

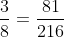
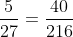
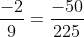
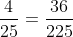
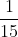
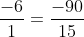
$\frac{3}{8} = \frac{81}{216}$ $\frac{5}{27} = \frac{40}{216}$ $\frac{-2}{9} = \frac{-50}{225}$ $\frac{4}{25} = \frac{36}{225}$ $\frac{1}{15}$ $\frac{-6}{1} = \frac{-90}{15}$

Bài 3:

Quy đồng mẫu các phân số dưới đây:

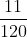
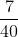
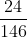
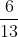
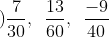
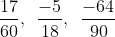
$\frac{11}{120}$ $\frac{7}{40}$ $\frac{24}{146}$ $\frac{6}{13}$ $\frac{7}{30}, \frac{13}{60}, \frac{-9}{40}$ $\frac{17}{60}, \frac{-5}{18}, \frac{-64}{90}$

Hướng dẫn thực hiện:

Chuyển đổi các phân số đã cho về dạng tương ứng nhưng cùng có một mẫu số chung.

Giải quyết:

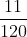
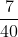
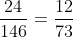
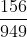
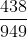
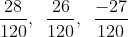
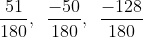
$\frac{11}{120}$ $\frac{7}{40}$ $\frac{24}{146} = \frac{12}{73}$ $\frac{156}{949}$ $\frac{438}{949}$ $\frac{28}{120},\,\,\,\frac{26}{120},\,\,\,\frac{-27}{120}$ $\frac{51}{180},\,\,\,\frac{-50}{180},\,\,\,\frac{-128}{180}$

Bài 4:

Liệu hai phân số dưới đây có bằng nhau không?

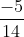
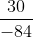
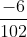
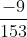
$\frac{-5}{14}$ $\frac{30}{-84}$ $\frac{-6}{102}$ $\frac{-9}{153}$

Hướng dẫn:

Thực hiện rút gọn các phân số để so sánh chúng khi ở dạng tối giản nhất.

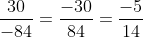
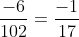
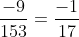
$\frac{30}{-84} = \frac{-30}{84} = \frac{-5}{14}$ $\frac{-6}{102} = \frac{-1}{17}$ $\frac{-9}{153} = \frac{-1}{17}$

Bài 5

Quy đồng mẫu cho các phân số sau:

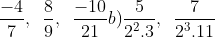
$\frac{-4}{7},\,\,\,\frac{8}{9},\,\,\,\frac{-10}{21} b) \frac{5}{2^2 \cdot 3},\,\,\,\frac{7}{2^3 \cdot 11}$

Hướng dẫn:

Để quy đồng mẫu cho nhiều phân số có mẫu số dương, thực hiện các bước sau:

+ Bước 1: Tìm bội chung nhỏ nhất của các mẫu số để làm mẫu số chung.

+ Bước 2: Xác định thừa số phụ của từng mẫu số (bằng cách chia mẫu số chung cho từng mẫu số).

+ Bước 3: Nhân cả tử số và mẫu số của mỗi phân số với thừa số phụ tương ứng.

Lời giải:

a) Với BCNN (7, 9, 21) = 63, ta có mẫu số chung của các phân số là 63.

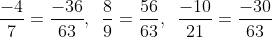
$\frac{{ - 4}}{7} = \frac{{ - 36}}{{63}},\,\,\,\frac{8}{9} = \frac{{56}}{{63}},\,\,\,\frac{{ - 10}}{{21}} = \frac{{ - 30}}{{63}}$

b) Với BCNN (22.3, 23.11) = 23 . 3 . 11 = 264, mẫu số chung của các phân số là 264.

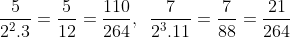
$\frac{5}{{{2^2}.3}} = \frac{5}{{12}} = \frac{{110}}{{264}},\,\,\,\frac{7}{{{2^3}.11}} = \frac{7}{{88}} = \frac{{21}}{{264}}$

Bài 6:

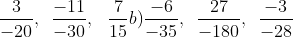
$\frac{3}{{ - 20}},\,\,\,\frac{{ - 11}}{{ - 30}},\,\,\,\frac{7}{{15}} b) \frac{{ - 6}}{{ - 35}},\,\,\,\frac{{27}}{{ - 180}},\,\,\,\frac{{ - 3}}{{ - 28}}$

Hướng dẫn:

Để quy đồng mẫu số cho nhiều phân số có mẫu số dương, thực hiện các bước sau:

+ Bước 1: Xác định bội chung nhỏ nhất của các mẫu số (thường là BCNN) để làm mẫu số chung.

+ Bước 2: Tìm thừa số bổ sung của từng mẫu số bằng cách chia mẫu số chung cho mỗi mẫu số.

+ Bước 3: Nhân cả tử và mẫu của mỗi phân số với hệ số bổ sung tương ứng.

Lời giải:

a) Mẫu số chung cho các phân số là 60.

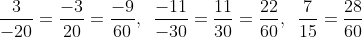
$\frac{3}{{ - 20}} = \frac{{ - 9}}{{60}},\,\,\,\frac{{ - 11}}{{ - 30}} = \frac{{22}}{{60}},\,\,\,\frac{7}{{15}} = \frac{{28}}{{60}}$

b) Mẫu số chung cho các phân số là 420.

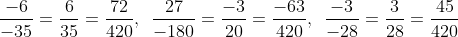
$\frac{{ - 6}}{{ - 35}} = \frac{6}{{35}} = \frac{{72}}{{420}},\,\,\,\frac{{27}}{{ - 180}} = \frac{{ - 63}}{{420}},\,\,\,\frac{{ - 3}}{{ - 28}} = \frac{3}{{28}} = \frac{{45}}{{420}}$

Bài 7:

Đưa các phân số về cùng một mẫu số:

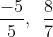
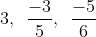
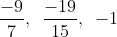
$\frac{{ - 5}}{5},\,\,\,\frac{8}{7}$ $3,\,\,\,\frac{{ - 3}}{5},\,\,\,\frac{{ - 5}}{6}$ $\frac{{ - 9}}{7},\,\,\,\frac{{ - 19}}{{15}},\,\,\, - 1$

Hướng dẫn:

Chuyển đổi các phân số đã cho sao cho tất cả đều có cùng một mẫu số.

Lời giải:

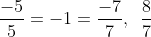
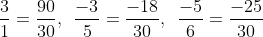
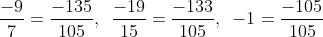
$\frac{{ - 5}}{5} = - 1 = \frac{{ - 7}}{7},\,\,\,\frac{8}{7}$ $\frac{3}{1} = \frac{{90}}{{30}},\,\,\,\frac{{ - 3}}{5} = \frac{{ - 18}}{{30}},\,\,\,\frac{{ - 5}}{6} = \frac{{ - 25}}{{30}}$ $\frac{{ - 9}}{7} = \frac{{ - 135}}{{105}},\,\,\,\frac{{ - 19}}{{15}} = \frac{{ - 133}}{{105}},\,\,\, - 1 = \frac{{ - 105}}{{105}}$

Bài 8:

Rút gọn và quy đồng mẫu cho các phân số sau:

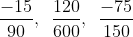
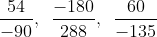
$\frac{{ - 15}}{{90}},\,\,\,\frac{{120}}{{600}},\,\,\,\frac{{ - 75}}{{150}}$ $\frac{{54}}{{ - 90}},\,\,\,\frac{{ - 180}}{{288}},\,\,\,\frac{{60}}{{ - 135}}$

Hướng dẫn:

Chuyển đổi các phân số đã cho sao cho chúng có cùng mẫu số, sau đó thực hiện các phép biến đổi cần thiết.

Lời giải:

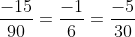
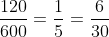
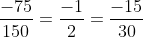
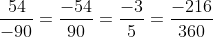
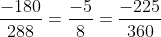
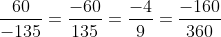
$\frac{{ - 15}}{{90}} = \frac{{ - 1}}{6} = \frac{{ - 5}}{{30}}$ $\frac{{120}}{{600}} = \frac{1}{5} = \frac{6}{{30}}$ $\frac{{ - 75}}{{150}} = \frac{{ - 1}}{2} = \frac{{ - 15}}{{30}}$ $\frac{{54}}{{ - 90}} = \frac{{ - 54}}{{90}} = \frac{{ - 3}}{5} = \frac{{ - 216}}{{360}}$ $\frac{{ - 180}}{{288}} = \frac{{ - 5}}{8} = \frac{{ - 225}}{{360}}$ $\frac{{60}}{{ - 135}} = \frac{{ - 60}}{{135}} = \frac{{ - 4}}{9} = \frac{{ - 160}}{{360}}$ $\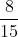frac{8}{{15}}$ $\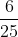frac{6}{{25}}$

Lời giải:

Có 75 chia cho 15 bằng 5 và 75 chia cho 25 bằng 3

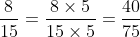
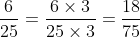
$\frac{8}{{15}} = \frac{{8 \times 5}}{{15 \times 5}} = \frac{{40}}{{75}}$ $\frac{6}{{25}} = \frac{{6 \times 3}}{{25 \times 3}} = \frac{{18}}{{75}}$

Bài 10: Quy đồng mẫu số cho các phân số sau đây:

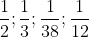
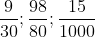
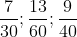
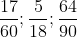
$\frac{1}{2}; \frac{1}{3}; \frac{1}{{38}}; \frac{1}{{12}}$ $\frac{9}{{30}}; \frac{{98}}{{80}}; \frac{{15}}{{1000}}$ $\frac{7}{{30}}; \frac{{13}}{{60}}; \frac{9}{{40}}$ $\frac{{17}}{{60}}; \frac{5}{{18}}; \frac{{64}}{{90}}$

Chi tiết lời giải:

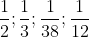
$\frac{1}{2}; \frac{1}{3}; \frac{1}{{38}}; \frac{1}{{12}}$

Mẫu số chung của các phân số là 228.

Các phép chia là: 228 : 2 = 114; 228 : 3 = 76; 228 : 38 = 6; 228 : 12 = 19

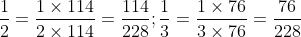
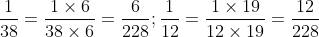
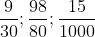
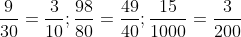
$\frac{1}{2} = \frac{{1 \times 114}}{{2 \times 114}} = \frac{{114}}{{228}}; \frac{1}{3} = \frac{{1 \times 76}}{{3 \times 76}} = \frac{{76}}{{228}}$ $\frac{1}{{38}} = \frac{{1 \times 6}}{{38 \times 6}} = \frac{6}{{228}}; \frac{1}{{12}} = \frac{{1 \times 19}}{{12 \times 19}} = \frac{{19}}{{228}}$ $\frac{9}{{30}}; \frac{{98}}{{80}}; \frac{{15}}{{1000}}$ $\frac{9}{{30}} = \frac{3}{{10}}; \frac{{98}}{{80}} = \frac{{49}}{{40}}; \frac{{15}}{{1000}} = \frac{3}{{200}}$

Mẫu số chung của các phân số là 200.

Có 200 chia cho 10 bằng 20; 200 chia cho 40 bằng 5.

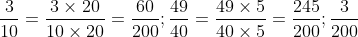
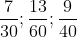
$\frac{3}{{10}} = \frac{{3 \times 20}}{{10 \times 20}} = \frac{{60}}{{200}}; \frac{{49}}{{40}} = \frac{{49 \times 5}}{{40 \times 5}} = \frac{{245}}{{200}}; \frac{3}{{200}}$ $\frac{7}{{30}}; \frac{{13}}{{60}}; \frac{9}{{40}}$

Mẫu số chung của các phân số là 120.

Có 120 chia cho 30 bằng 4; 120 chia cho 60 bằng 2; 120 chia cho 40 bằng 3.

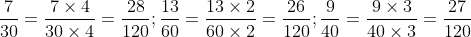
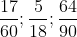
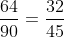
$\frac{7}{{30}} = \frac{{7 \times 4}}{{30 \times 4}} = \frac{{28}}{{120}}; \frac{{13}}{{60}} = \frac{{13 \times 2}}{{60 \times 2}} = \frac{{26}}{{120}}; \frac{9}{{40}} = \frac{{9 \times 3}}{{40 \times 3}} = \frac{{27}}{{120}}$ $\frac{{17}}{{60}}; \frac{5}{{18}}; \frac{{64}}{{90}}$ $\frac{{64}}{{90}} = \frac{{32}}{{45}}$

Mẫu số chung của các phân số là 180.

Có 180 chia cho 60 bằng 3; 180 chia cho 18 bằng 10; 180 chia cho 45 bằng 4.

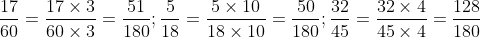
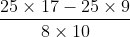
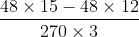
$\frac{{17}}{{60}} = \frac{{17 \times 3}}{{60 \times 3}} = \frac{{51}}{{180}}; \frac{5}{{18}} = \frac{{5 \times 10}}{{18 \times 10}} = \frac{{50}}{{180}}; \frac{{32}}{{45}} = \frac{{32 \times 4}}{{45 \times 4}} = \frac{{128}}{{180}}$ $\frac{{25 \times 17 - 25 \times 9}}{{8 \times 10 + 8 \times 10}}$ $\frac{{48 \times 15 - 48 \times 12}}{{270 \times 3 + 30 \times 3}}$

Lời giải:

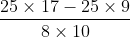
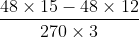
$\frac{{25 \times 17 - 25 \times 9}}{{8 \times 10 + 8 \times 10}} = \frac{{25 \times (17 - 9)}}{{2 \times 8 \times 10}} = \frac{{25 \times 8}}{{2 \times 8 \times 10}} = \frac{5}{4}$ $\frac{{48 \times 15 - 48 \times 12}}{{270 \times 3 + 30 \times 3}} = \frac{{48 \times (15 - 12)}}{{90 \times (9 + 1)}} = \frac{{48 \times 3}}{{90 \times 10}} = \frac{4}{{25}}$

Mẫu số chung của hai phân số là: 100

100 chia cho 4 bằng 25 và 100 chia cho 25 bằng 4

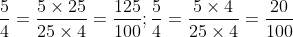
$\frac{5}{4} = \frac{{5 \times 25}}{{25 \times 4}} = \frac{{125}}{{100}}; \frac{5}{4} = \frac{{5 \times 4}}{{25 \times 4}} = \frac{{20}}{{100}}$

Bài 12:

Chuyển đổi các phân số về cùng một mẫu số:

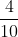
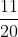
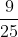
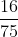
$\frac{7}{9}$ $\frac{2}{3}$ $\frac{4}{10}$ $\frac{11}{20}$ $\frac{9}{25}$ $\frac{16}{75}$

Cách giải:

Để đồng nhất mẫu số của hai phân số, khi mẫu số của một trong số đó đã là mẫu số chung (MSC), ta thực hiện như sau:

– Tìm mẫu số chung

– Tính thương của mẫu số chung và mẫu số của phân số còn lại.

– Nhân thương vừa tính với tử số và mẫu số của phân số còn lại. Giữ nguyên phân số có mẫu số là mẫu số chung.

Kết quả:

Các bạn đồng nhất mẫu số như sau:

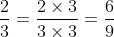
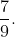
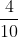
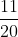
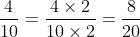
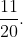
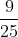
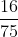
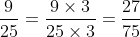
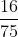
$\frac{7}{9}$ $\frac{2}{3}$ $\frac{2}{3}=\frac{2 \times 3}{3 \times 3}=\frac{6}{9}$ $\frac{7}{9}.$ $\frac{4}{10}$ $\frac{11}{20}$ $\frac{4}{10}=\frac{4 \times 2}{10 \times 2}=\frac{8}{20}$ $\frac{11}{20}.$ $\frac{9}{25}$ $\frac{16}{75}$ $\frac{9}{25}=\frac{9 \times 3}{25 \times 3}=\frac{27}{75}$ $\frac{16}{75}$

Bài 12:

Chuyển các phân số sau đây về dạng phân số có mẫu số chung là 24:

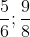
$\frac{5}{6};\frac{9}{8}$

Cách giải:

$\frac{5}{6}$ $\frac{9}{8}$

Kết quả:

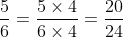
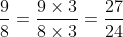
$\frac{5}{6}$ $\frac{5}{6} = \frac{5 \times 4}{6 \times 4} = \frac{20}{24}$ $\frac{9}{8}$ $\frac{9}{8} = \frac{9 \times 3}{8 \times 3} = \frac{27}{24}$

Bài viết từ Mytour mong rằng đã cung cấp thông tin bổ ích cho quý độc giả.

Nội dung từ Mytour nhằm chăm sóc khách hàng và khuyến khích du lịch, chúng tôi không chịu trách nhiệm và không áp dụng cho mục đích khác.

Nếu bài viết sai sót hoặc không phù hợp, vui lòng liên hệ qua email: [email protected]