Bài tập Toán lớp 7: Tính tổng ba góc trong một tam giác và đáp án

Buzz

Nội dung bài viết

A. Kiến thức về tổng các góc trong tam giác

B. Bài tập toán liên quan đến tổng ba góc trong tam giác

Xem thêm

Bài viết dưới đây cung cấp bài tập toán lớp 7 về tổng ba góc của tam giác, bao gồm đáp án và hướng dẫn giải chi tiết

A. Kiến thức về tổng các góc trong tam giác

1. Định lý về tổng ba góc trong tam giác:

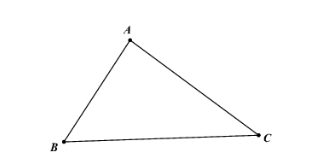
Bài tập Toán lớp 7: Tính tổng ba góc trong tam giác và đáp án

Tổng ba góc của tam giác luôn bằng 180^o

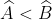
$widehat{A} + widehat{B} + widehat{C} = 180^{o}$

2. Ứng dụng trong tam giác vuông

- Định nghĩa: tam giác vuông là tam giác có một góc vuông

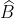
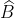
$widehat{B} + widehat{C} = 90^{o}$ $widehat{B} + widehat{C} = 90^{o}$

3. Góc ngoài của tam giác

- Định nghĩa: Góc ngoài của tam giác là góc kề bù với một góc bên trong của tam giác

- Tính chất: Mỗi góc ngoài của tam giác bằng tổng của hai góc trong không kề với nó

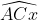
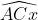
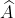
4. Các loại bài tập

Dạng 1: Xác định số đo của một góc và so sánh các góc

Phương pháp giải:

- Thiết lập đẳng thức cho bài toán:

+ Tổng ba góc của tam giác luôn bằng 180^o

+ Trong tam giác vuông, hai góc nhọn bổ sung cho nhau

+ Góc ngoài của tam giác bằng tổng của hai góc trong không kề với nó

- Tính số đo của góc cần tìm sau đó

Dạng 2: Các bài toán chứng minh các góc

Phương pháp giải:

Áp dụng linh hoạt các định lý về góc trong tam giác, góc ngoài tại một đỉnh, hoặc tính chất của tia phân giác

- Bước 1: Sử dụng định lý tổng ba góc trong tam giác, góc ngoài tại một đỉnh, hoặc tính chất của tia phân giác để tính toán

- Bước 2: Dùng tính chất của tia phân giác để chứng minh các hệ thức

B. Bài tập toán liên quan đến tổng ba góc trong tam giác

Câu hỏi 1: Tính số đo của các góc còn lại trong từng tam giác của các hình vẽ dưới đây

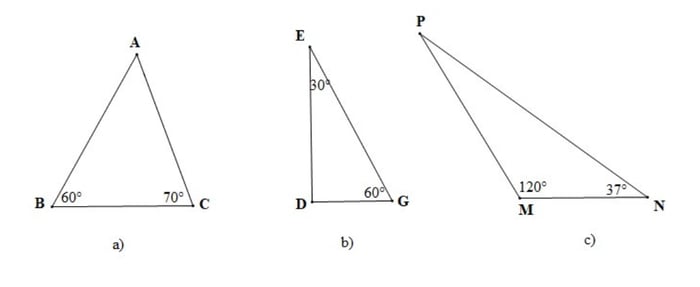
Bài tập Toán lớp 7: Tổng ba góc trong tam giác và đáp án

Hướng dẫn giải chi tiết:

- Hình a)

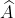
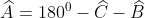
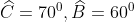
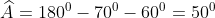
$widehat{A} + widehat{B} + widehat{C} = 180^{0}$ $widehat{A} = 180^{0} - widehat{B} - widehat{C}$ $widehat{C} = 70^{0}, widehat{B} = 60^{0}$ $widehat{A} = 180^{0} - 70^{0} - 60^{0} = 50^{0}$

Vậy số đo của góc A là 50^o

- Hình b)

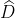
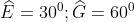
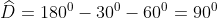
$widehat{E} = 30^{0}; widehat{G} = 60^{0}$ $widehat{D} = 180^{0} - 30^{0} - 60^{0} = 90^{0}$

Vậy số đo của góc D là 90^o

- Hình c)

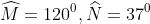
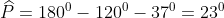
$widehat{M} = 120^{0}, widehat{N} = 37^{0}$ $widehat{P} = 180^{0} - 120^{0} - 37^{0} = 23^{0}$

Vậy số đo của góc P là 23⁰

Chú ý:

- Tam giác có ba góc đều nhọn được gọi là tam giác nhọn

- Tam giác có một góc vuông được gọi là tam giác vuông

- Tam giác có một góc tù được gọi là tam giác tù

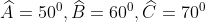
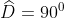
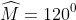
$widehat{A} = 50^{0}, widehat{B} = 60^{0}, widehat{C} = 70^{0}$ $widehat{D} = 90^{0}$ $widehat{M} = 120^{0}$

Câu hỏi 2: Một chiếc thang dựa vào tường có góc nghiêng so với mặt đất là 70^o. Vậy góc nghiêng của thang với bức tường là bao nhiêu?

Giải chi tiết:

Vẽ tam giác vuông ABC (như hình vẽ) để minh họa vị trí của chiếc thang dựa vào tường.

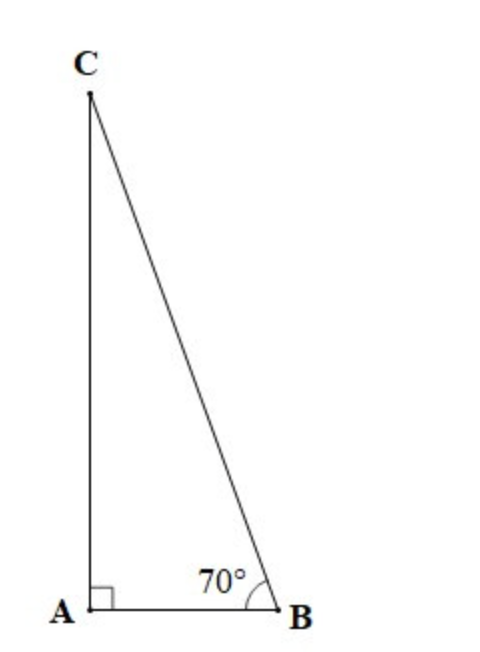
Bài tập Toán lớp 7: Tổng ba góc của một tam giác có đáp án

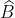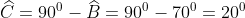
$widehat{B} + widehat{C} = 90^{0}$ ^độ $widehat{C} = 90^{0} - widehat{B} = 90^{0} - 70^{0} = 20^{0}$

Vậy góc nghiêng của chiếc thang với bức tường là 20

Chú ý về góc ngoài của tam giác

- Góc ngoài của tam giác là góc kề bù với một góc bên trong của tam giác đó

- Mỗi góc ngoài của tam giác bằng tổng của hai góc bên trong không kề với nó

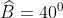
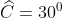
$widehat{B} = 40^{0}$ $widehat{C} = 30^{0}$

Lời giải chi tiết:

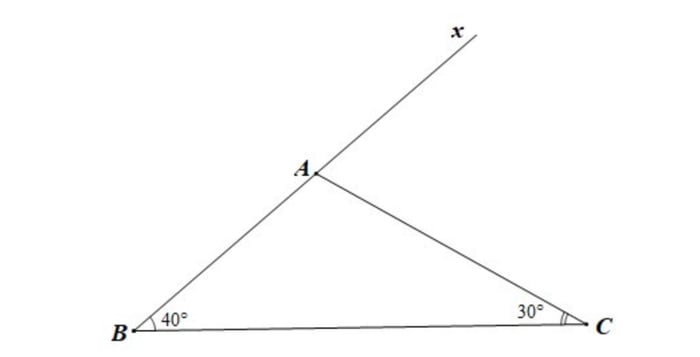
Bài tập Toán lớp 7: Đáp án cho tổng ba góc của một tam giác

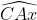
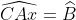
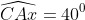
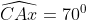
$widehat{CAx} = 40^{0} + 30^{0} = 70^{0}$ $widehat{CAx} = 70^{0}$

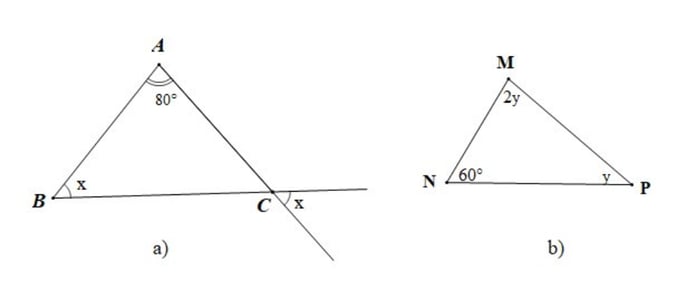
Câu hỏi 4: Xác định giá trị của góc x và y trong các hình vẽ sau:

Bài tập Toán lớp 7: Đáp án tổng ba góc của tam giác

Lời giải chi tiết:

- Hình A

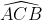
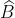
$widehat{A} + widehat{B} + widehat{ACB} = 180^{0}$ $widehat{B} + widehat{ACB} = 180^{0} - widehat{A}$ $widehat{A} = 80^{0}, widehat{B} và widehat{ACB} đều bằng x$

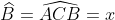
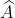
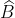
Vì vậy, x + x = 180^o - 80^o

Hay 2x = 100^o

Do đó, x = 50^o

- Hình b)

$widehat{M} + widehat{N} + widehat{P} = 180^{0}$

Vậy y + 2y + 60^o = 180^o

Do đó, 3y = 180^o - 60^o

3y = 120^o

Suy ra, y = 120^o / 3 = 40^o

Vậy y = 40^o

Câu hỏi 5: Xác định số đo của góc ABC trong hình dưới đây, với điều kiện Ax // Cy

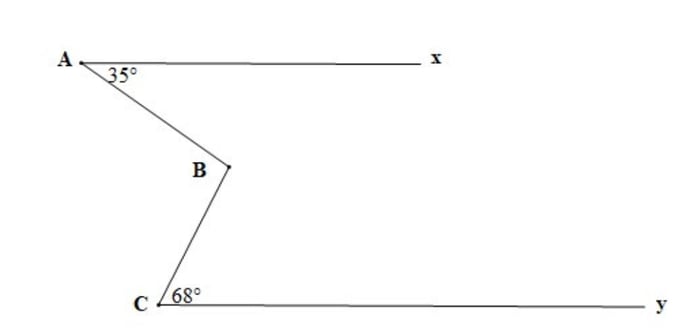
Bài tập Toán lớp 7: Tổng ba góc của một tam giác với đáp án

Lời giải chi tiết

Ký hiệu giao điểm của AB và đường thẳng Cy là D, ta có hình minh họa như sau:

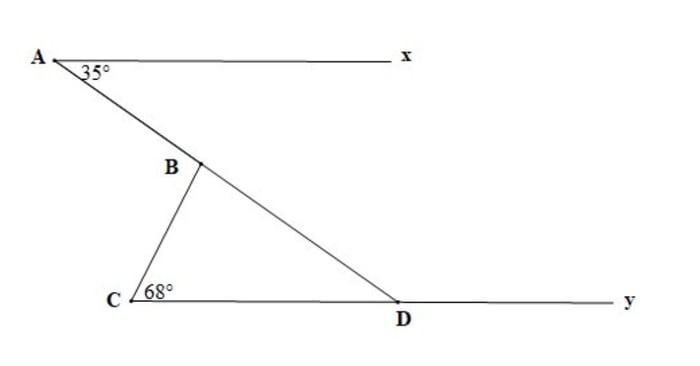
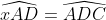
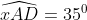
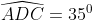
$widehat{xAD} = 35^{0}$ $widehat{ADC} = 35^{0}$

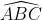
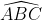
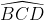
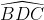
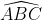^góc^góc^góc

Số đo góc ABC là 103^o

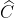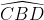^góc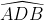

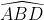
Chi tiết giải bài:

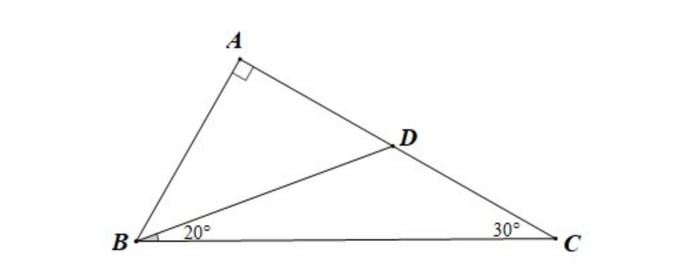
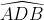
widehat{ADB} = widehat{C} + widehat{CBD}

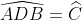
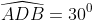
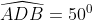
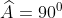
$widehat{ADB} = 30^{0} + 20^{0} = 50^{0}$ $widehat{ADB} = 50^{0}$ $widehat{A} = 90^{0}$

Vậy tam giác ABD là tam giác vuông tại A

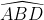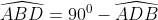
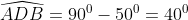
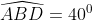
$widehat{ABD} + widehat{ADB} = 90^{0}$ ^o $widehat{ABD} = 90^{0} - widehat{ADB}$ $widehat{ADB} = 90^{0} - 50^{0} = 40^{0}$ $widehat{ABD} = 40^{0}$

Câu hỏi 7: Một chiếc thang dựa vào tường, với góc nghiêng so với mặt đất là 57^o. Hãy tìm góc nghiêng của chiếc thang so với bức tường:

A. 55^o

B. 44^o

C. 33^o

D. 22^o

Giải chi tiết:

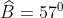
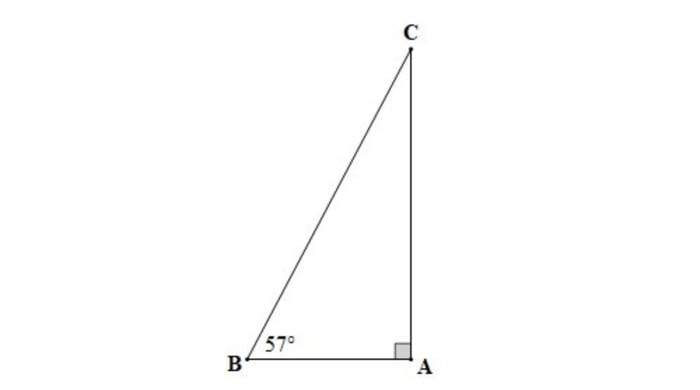
$widehat{B} = 57^{0}$ Bài tập Toán lớp 7: Tổng ba góc của một tam giác với đáp án

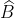
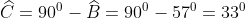
$widehat{B} + widehat{C} = 90^{0}$ $widehat{C} = 90^{0} - widehat{B} = 90^{0} - 57^{0} = 33^{0}$

Do đó, góc nghiêng của chiếc thang so với bức tường là 33^o.

Vì vậy, đáp án chính xác là C

Câu hỏi 8: Xem hình vẽ dưới đây

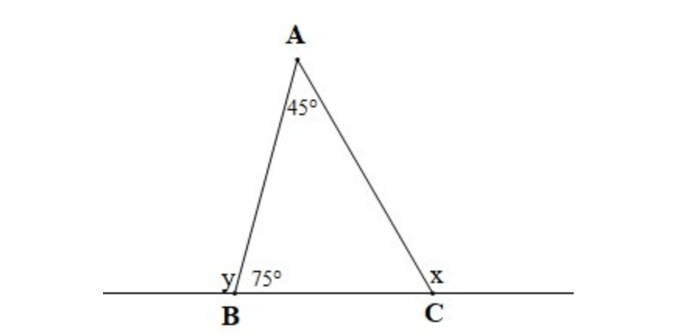
Các giá trị của x và y lần lượt là:

A. 105^o và 120^o

B. 120^o và 105^o

C. 102^o và 150^o

D. 150^o và 102^o

Hướng dẫn chi tiết:

Trong tam giác ABC, góc x là góc ngoài tại đỉnh C

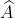
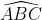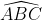Vì vậy, x = 45^o + 75^o = 120^o

^o^o

^o^o^o

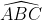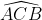Do đó, góc x và y lần lượt là 120^o và 105^o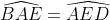

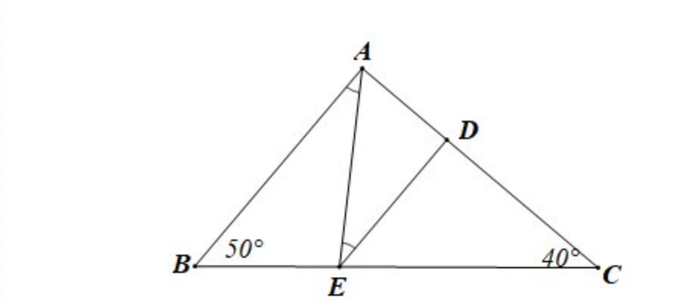
Tam giác CDE thuộc loại nào?

A. Tam giác nhọn

B. Tam giác đều

C. Tam giác vuông

D. Tam giác tù

Lời giải chi tiết:

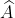
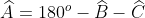
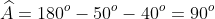
$widehat{A} = 180^{o} - widehat{B} - widehat{C}$ $widehat{A} = 180^{o} - 50^{o} - 40^{o} = 90^{o}$

Hai góc này nằm đối diện nhau và đối xứng qua đường thẳng

Do đó, DE song song với AB

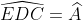
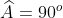
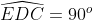
$widehat{A} = 90^{o}$ $widehat{EDC} cũng bằng 90^{o}$

Do đó, tam giác CDE là một tam giác vuông

Câu hỏi 10: Đưa ra kết luận chính xác sau đây

A. Một tam giác có thể có tối đa hai góc nhọn

B. Một tam giác chỉ có thể có một góc tù

C. Trong một tam giác, luôn có ít nhất hai góc nhỏ hơn 60^o

D. Trong một tam giác, số đo của mỗi góc luôn nhỏ hơn tổng số đo của hai góc còn lại

Lời giải chi tiết:

A. Sai. Có thể tạo ra tam giác với ba góc nhọn, chẳng hạn tam giác với mỗi góc là 60^o

B. Đúng. Nếu tam giác có nhiều hơn một góc tù, tổng ba góc sẽ lớn hơn 180^o (trái với định lý tổng ba góc trong tam giác). Vì vậy, một tam giác chỉ có thể có tối đa một góc tù

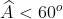
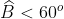
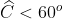
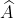
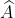$widehat{A} < 60^{o}$ $widehat{B} < 60^{o}$ $widehat{C} < 60^{o}$ $widehat{A} + widehat{B} + widehat{C} < 180^{o}$

₁

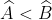
widehat{A} < widehat{B} + widehat{C} = widehat{A}

Câu hỏi 11: Tòa tháp Capital Gate (thuộc Các tiểu vương quốc Ả Rập Thống nhất) nghiêng 18^o so với phương thẳng đứng (như trong Hình 1). Tính đến ngày 01/6/2020, đây là tòa tháp nghiêng nhiều nhất thế giới. Làm thế nào để xác định độ nghiêng của tòa tháp Capital Gate so với phương nằm ngang?

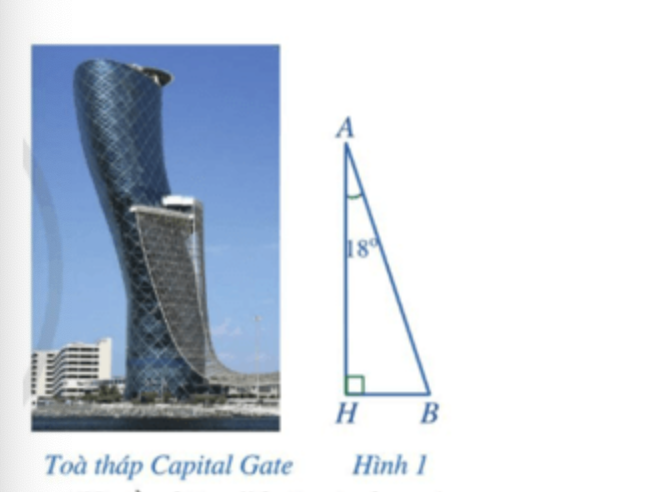
Bài tập Toán lớp 7: Tổng ba góc của một tam giác và đáp án

Chi tiết giải thích:

Áp dụng định lý tổng ba góc trong tam giác, chúng ta tính tổng ba góc của tam giác, sau đó trừ đi số đo góc vuông và góc 18^o so với phương thẳng đứng để tìm độ nghiêng của tòa tháp so với phương nằm ngang.

Cụ thể như sau:

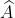
$widehat{A} + widehat{H} + widehat{B} = 180^{o}$

Kết luận

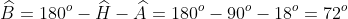
$widehat{B} = 180^{o} - widehat{H} - widehat{A} = 180^{o} - 90^{o} - 18^{o} = 72^{o}$

Do đó, độ nghiêng của tòa tháp Capital Gate so với phương nằm ngang là 72^o

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]