Bài tập về các trường hợp tam giác có cạnh bằng nhau trong Ôn tập Hình học lớp 7

Buzz

Nội dung bài viết

1. Các trường hợp tam giác bằng nhau

2. Ứng dụng của các trường hợp tam giác bằng nhau

3. Bài tập về các trường hợp tam giác bằng nhau

Xem thêm

Đọc tóm tắt

- Tài liệu bài tập về các trường hợp tam giác có cạnh bằng nhau dành cho học sinh lớp 7 bao gồm lý thuyết, các dạng bài tập và phương pháp giải với đáp án mẫu.
- Các trường hợp tam giác bằng nhau được phân loại thành ba loại: ba cạnh bằng nhau (c-c-c), cạnh-góc-cạnh (c-g-c), và góc-cạnh-góc (g-c-g). Tài liệu cũng cung cấp các bài tập tự luyện để củng cố kiến thức, giúp học sinh áp dụng lý thuyết vào thực hành và chuẩn bị tốt cho các bài kiểm tra, bao gồm bài tập về chứng minh các tam giác bằng nhau, tính toán độ dài đoạn thẳng, góc, và các bài tập so sánh.

Bài tập về các trường hợp tam giác có cạnh bằng nhau là tài liệu quan trọng không thể thiếu cho học sinh lớp 7.

Bài tập về các trường hợp tam giác có cạnh bằng nhau bao gồm lý thuyết đầy đủ, các dạng bài tập và phương pháp giải cùng đáp án mẫu cho một số bài tập tự luyện. Tài liệu được biên soạn cẩn thận, phù hợp với mọi học sinh từ trung bình đến giỏi. Nó giúp học sinh củng cố và hiểu rõ kiến thức cơ bản, áp dụng vào các bài tập để đạt điểm cao trong kiểm tra. Ngoài ra, học sinh cũng có thể xem thêm tài liệu về tìm nghiệm của đa thức và cách chứng minh ba điểm thẳng hàng.

1. Các trường hợp tam giác bằng nhau

a) Trường hợp 1: Ba cạnh bằng nhau: Nếu ba cạnh của một tam giác bằng ba cạnh của một tam giác khác, thì hai tam giác đó là bằng nhau.

b) Trường hợp 2: Cạnh – Góc – Cạnh: Nếu hai cạnh và góc nằm giữa của tam giác này bằng với hai cạnh và góc nằm giữa của tam giác kia, thì hai tam giác đó là bằng nhau.

c) Trường hợp 3: Góc – Cạnh – Góc: Nếu một cạnh và hai góc kề nhau của tam giác này bằng với một cạnh và hai góc kề nhau của tam giác kia, thì hai tam giác đó là bằng nhau.

2. Ứng dụng của các trường hợp tam giác bằng nhau

Chúng ta thường áp dụng các trường hợp tam giác bằng nhau để:

Chứng minh: hai tam giác bằng nhau, hai đoạn thẳng bằng nhau, hai góc bằng nhau; hai đường thẳng vuông góc; hai đường thẳng song song; ba điểm thẳng hàng; …
Tính: các độ dài đoạn thẳng; tính số đo góc; tính chu vi; diện tích; …
So sánh: các độ dài đoạn thẳng; so sánh các góc; …

3. Bài tập về các trường hợp tam giác bằng nhau

A. Bài tập có câu trả lời

a) Trường hợp 1: Cạnh – Cạnh – Cạnh

Bài 1: Cho tam giác ABC. Vẽ cung tròn có tâm là A và bán kính là BC, vẽ cung tròn có tâm là C và bán kính là BA, chúng cắt nhau tại điểm D (D và B nằm ở hai bên khác nhau so với đường AC). Chứng minh rằng AD // BC

Gợi ý cho câu trả lời

Xét tam giác ABC và tam giác CDA có cạnh AC chung

AB bằng CD (đề cho)

BC bằng DA (đề cho)

Do đó tam giác ABC bằng tam giác CDA (c-c-c)

trong trường hợp hai góc đối diện là bằng nhau

Do đó ta có AD // BC

Bài 2: Tam giác ABC có AB = AC, M là trung điểm của BC. Chứng minh rằng AM vuông góc với BC.

Gợi ý cho câu trả lời

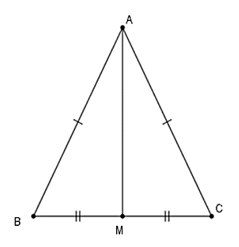
Xét tam giác AMB và tam giác AMC có:

AB bằng AC

AM là cạnh chung

MB bằng MC (đề cho)

⇒ Tam giác AMB bằng tam giác AMC (c-c-c)

Góc BAM bằng góc CAM; Góc AMB bằng góc AMC

Góc AMB bằng góc AMC bằng một nửa của 180 độ, tức là 90 độ

b) Trường hợp 2: Cạnh – Góc – Cạnh

Bài 1: Cho đoạn thẳng BC. Gọi A là một điểm nằm trên đường thẳng vuông góc với BC tại M. Chứng minh AB bằng AC

Giải thích

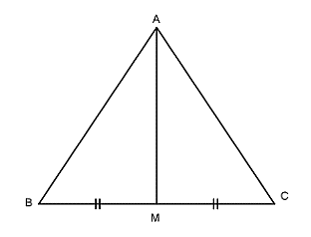
Xét hai tam giác AMB và AMC có:

MB bằng MC (đề cho)

AH là cạnh chung

Do đó tam giác AMB bằng tam giác AMC (c-g-c)

⇒ AB bằng AC (theo hai cạnh tương ứng)

Bài 2: Cho đường thẳng AB, trên hai mặt phẳng đối diện của nó vẽ hai tia Ax vuông góc với AB; By vuông góc với BA. Trên Ax và By lần lượt chọn hai điểm C và D sao cho AC bằng BD. Gọi O là trung điểm của AB.

a) Chứng minh rằng: Tam giác AOC bằng tam giác BOD

b) Chứng minh rằng O là trung điểm của CD

Gợi ý cho câu trả lời

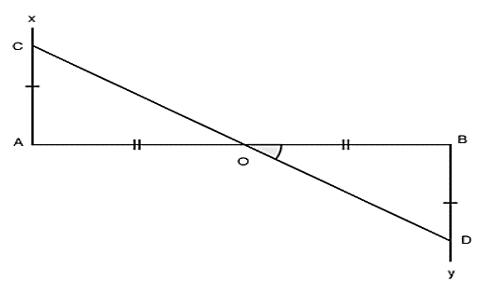
a) Xét tam giác AOC và tam giác BOD có:

OA bằng OB (đề cho)

AC bằng BD (đề cho)

Do đó tam giác AOC bằng tam giác BOD (c - g - c)

b) Vì tam giác AOC bằng tam giác BOD (chú thích)

$\Rightarrow Góc AOC bằng góc BOD; OC bằng OD$

Vì tia OC và OD nằm ở hai phía đối diện so với AB nên suy ra O, C, D thẳng hàng (hai tia đối của hai góc đối đỉnh hoặc O ở giữa CD)

Ta có: O ở giữa C và D nên OC bằng OD tức là O là trung điểm của CD

c) Trường hợp 3: Góc – Cạnh – Góc:

Bài 1:

Giải thích:

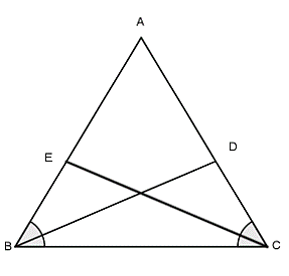
Xét tam giác EBC và tam giác DCB có:

BC là cạnh chung

Từ đó suy ra tam giác EBC bằng tam giác DCB (g - c - g)

Từ đó suy ra BD bằng CE (hai cạnh tương ứng bằng nhau)

B. Bài tập tự luyện

Câu 1: Nêu các trường hợp tam giác bằng nhau? Vẽ hình minh họa cho từng trường hợp?

Câu 2: Nêu các trường hợp tam giác vuông bằng nhau? Vẽ hình minh họa cho từng trường hợp?

Câu 3: Nêu định lí một đường thẳng vuông góc với một trong hai đường thẳng song song? Ghi giả thiết và kết luận? Vẽ hình minh họa?

Câu 4: Nêu định lí hai đường thẳng cùng vuông góc với một đường thẳng? Ghi giả thiết và kết luận? Vẽ hình minh họa?

Câu 5: Nêu định lí ba đường thẳng song song? Ghi giả thiết và kết luận? Vẽ hình minh họa?

Câu 6: Tìm hiểu các t/c, định lí liên quan đến các trường hợp bằng nhau của tam giác? Liệt kê tên?

Sau khi hiểu rõ các lý thuyết trên về các trường hợp bằng nhau của tam giác, hãy làm các bài tập dưới đây:

B. Bài tập tự luyện

Bài 1: Cho tam giác ABC; M là trung điểm của BC; N nằm trong tam giác sao cho NB = NC.

Chứng minh: Tam giác NMB bằng tam giác NMC.

Bài 2. Cho tam giác ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng: Góc ABE bằng góc ACE

Bài 3. Cho tam giác ABC có góc A bằng 40⁰ , AB bằng AC. Gọi M là trung điểm của BC. Tính các góc của tam giác AMB và tam giác AMC.

Bài 4. Cho tam giác ABC có AB = AC. D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE.

a. Chứng minh góc EAB bằng góc DAC.

b. Gọi M là trung điểm của BC. Chứng minh AM là phân giác của góc DAE.

c. Giả sử góc DAE bằng 60⁰. Tính các góc còn lại của tam giác DAE.

Bài 5. Cho tam giác ABC có góc A bằng 90⁰. Vẽ AD ⊥ AB (D, C nằm khác phía đối với AB) và AD = AB. Vẽ AE ⊥ AC (E, B nằm khác phía đối với AC) và AE = AC. Biết DE = BC. Tính góc BAC.

Bài 6. Cho tam giác ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng:

a. ∆ABE = ∆ACE

b. AE là đường trung trực của đoạn thẳng BC.

Bài 7. Cho tam giác ABC có AB < AC. Kẻ tia phân giác AD của góc BAC (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:

a. ∆BDF = ∆EDC.

b. BF = EC.

c. F, D, E thẳng hàng.

d. AD ⊥ FC

Bài 8. Cho góc nhọn xOy. Trên tia Ox, lấy 2 điểm A và C. Trên tia Oy lấy 2 điểm B và D sao cho OA = OB; OC = OD. (A nằm giữa O và C; B nằm giữa O và D).

a. Chứng minh ∆OAD = ∆OBC

b. So sánh 2 góc CAD và CBD.

Bài 9. Cho ΔABC vuông ở A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.

a. Chứng minh ΔABC = ΔABD

b. Trên tia đối của tia AB, lấy điểm M. Chứng minh ΔMBD = ΔMBC.

Bài 10. Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kì. Chứng minh:

a. ΔAOI = ΔBOI.

b. AB ⊥ OI.

Bài 11. Cho ΔABC, M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm E sao cho ME = MA.

a. Chứng minh AC // BE.

b. Gọi I là một điểm trên AC, K là một điểm trên EB sao cho AI = EK. Chứng minh 3 điểm I, M, K thẳng hàng.

Bài 12. Trong tam giác ABC, chọn điểm M nằm giữa A và C sao cho AM là trung điểm của AC. Trên tia đối của tia MB, đặt điểm D sao cho BM = MD.

a/ Chứng minh : ΔABM = ΔCDM.

b/ Chứng minh : AB // CD

c/ Trên DC kéo dài lấy điểm N sao cho CD =CN (C ≠ N) chứng minh : BN // AC.

Bài 13: Trong tam giác ABC có AB = AC, trên cạnh AB chọn điểm M, trên cạnh AC chọn điểm N sao cho AM = AN. Gọi H là trung điểm của BC.

a/ Chứng minh : ΔABH = ΔACH.

b/ Gọi E là giao điểm của AH và NM. Chứng minh : ΔAME = ΔANE

c/ Chứng minh : MM // BC.

Bài 14 : Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D. Lấy E trên cạnh BC sao cho BE = AB.

a) Chứng minh : Δ ABD = Δ EBD.

b) Tia ED cắt BA tại M. Chứng minh: EC = AM

c) Nối AE. Chứng minh: góc AEC = góc EAM.

Bài 15 : Cho tam giác ABC vuông góc tại A có góc B = 530.

a) Tính góc C.

b) Trên cạnh BC, lấy điểm D sao cho BD = BA. Tia phân giác của góc B cắt cạnh AC ở điểm E. Chứng minh: ΔBEA = ΔBED.

c) Qua C, vẽ đường thẳng vuông góc với BE tại H. CH cắt đường thẳng AB tại F. CMR: ΔBHF = ΔBHC.

d) Chứng minh: ΔBAC = ΔBDF và D, E, F thẳng hàng.

Bài 16: Cho tam giác ABC (AB < AC). Tia phân giác của góc A cắt đường trung trực của BC tại I. Kẻ IH vuông góc AB tại H. IK vuông góc AC tại K.

a/ Chứng minh: BH = CK.

b/ Chứng minh: AHIK nội tiếp đường tròn và tìm tâm đường tròn đó

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]

Các câu hỏi thường gặp

Các trường hợp tam giác bằng nhau là gì và có ứng dụng như thế nào?

Tam giác có ba trường hợp bằng nhau: ba cạnh bằng nhau (c-c-c), cạnh-góc-cạnh (c-g-c), và góc-cạnh-góc (g-c-g). Chúng được ứng dụng để chứng minh tính bằng nhau của tam giác, đoạn thẳng, góc, đường thẳng vuông góc, đường thẳng song song, ba điểm thẳng hàng, cũng như tính chu vi, diện tích của tam giác.

Làm thế nào để chứng minh hai tam giác bằng nhau theo trường hợp ba cạnh bằng nhau?

Để chứng minh hai tam giác bằng nhau theo trường hợp ba cạnh bằng nhau (c-c-c), ta phải chỉ ra rằng ba cạnh của tam giác này tương ứng bằng ba cạnh của tam giác kia. Ví dụ, trong bài tập, tam giác ABC và tam giác CDA có ba cạnh tương ứng bằng nhau, do đó chúng bằng nhau.

Cách chứng minh tam giác vuông có cạnh vuông góc với đường thẳng như thế nào?

Để chứng minh tam giác vuông có cạnh vuông góc với đường thẳng, ta có thể áp dụng các trường hợp tam giác bằng nhau. Ví dụ, trong bài tập, tam giác AMB và tam giác AMC có cạnh vuông góc chung và các cạnh tương ứng bằng nhau, nên ta có thể chứng minh AM vuông góc với BC.

Có thể áp dụng các trường hợp tam giác bằng nhau để tính diện tích và chu vi không?

Có thể. Các trường hợp tam giác bằng nhau không chỉ giúp chứng minh tính bằng nhau của các tam giác mà còn được áp dụng để tính diện tích và chu vi, đặc biệt trong các bài toán có các cạnh và góc tương ứng bằng nhau.

Trong trường hợp nào tam giác có thể áp dụng phương pháp chứng minh theo cạnh – góc – cạnh?

Tam giác có thể áp dụng phương pháp chứng minh theo cạnh – góc – cạnh (c-g-c) khi hai cạnh và góc nằm giữa của tam giác này bằng với hai cạnh và góc nằm giữa của tam giác kia. Điều này giúp chứng minh rằng hai tam giác này bằng nhau, như trong bài tập với tam giác AMB và tam giác AMC.