Bài tập về đường thẳng vuông góc và đường thẳng song song lớp 7
Bài 1. Cho hai đường thẳng a và b, nếu a // c và b // c thì:
A. a vuông góc với b
B. a trùng với b
C. a cắt b
D. a song song với b
Hướng dẫn giải
Đáp án chính xác là: D. a song song với b
Nếu hai đường thẳng phân biệt đều song song với một đường thẳng thứ ba, thì chúng cũng sẽ song song với nhau.
Bài 2. Tia Ot nào trong các hình dưới đây là tia phân giác của góc xOy?
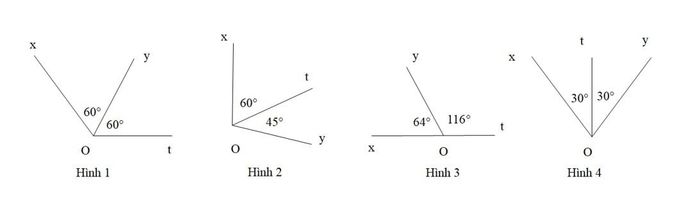
B. Hình 2;
C. Hình 3;
D. Hình 4.
Hướng dẫn giải
Câu trả lời chính xác là: D. Hình 4.
Tia phân giác của một góc là tia nằm bên trong góc và chia góc đó thành hai góc có độ lớn bằng nhau.
Tia Ot trong Hình 1 và Hình 3 không nằm trong góc xOy, vì vậy chúng không phải là tia phân giác của góc xOy.
Trong Hình 2, tia Ot nằm bên trong góc nhưng không chia góc đó thành hai góc bằng nhau. Do đó, tia Ot trong Hình 2 không phải là tia phân giác của góc xOy.
Chỉ có Hình 4 thể hiện tia Ot nằm trong góc và chia góc đó thành hai góc bằng nhau, nên tia Ot trong Hình 4 chính là tia phân giác của góc xOy.
Vì vậy, lựa chọn đúng là phương án D.
Bài 3. Cho tia Ot nằm trong góc mOn, với góc mOt bằng góc tOn thì:
A. Ot là tia phân giác của góc mOn;
B. Ot là tia nằm trong góc mOn;
C. Ot là tia nằm ngoài góc mOn;
D. Ot là tia nằm giữa hai cạnh Om và On.
Hướng dẫn giải
Đáp án chính xác là: A. Ot là tia phân giác của góc mOn;
Ot là tia nằm trong góc mOn và chia góc đó thành hai góc bằng nhau, với góc mOt bằng góc tOn, vì vậy Ot là tia phân giác của góc mOn.
Bài 4. Điền thông tin phù hợp vào chỗ trống:
Nếu góc xOt và góc tOy là hai góc kề bù thì tổng số đo của hai góc là 180 độ
(Giả thiết) (......)
A. kết luận;
B. khẳng định;
C. chứng minh;
D. Tất cả các đáp án đều chính xác.
Hướng dẫn giải
Đáp án đúng là: A. kết luận;
Phần giữa từ “Nếu” và từ “thì” là giả thiết, còn phần sau từ “thì” là kết luận.
Bài 5. Diễn đạt định lý dưới đây bằng lời văn.
- Giả thiết:
đường thẳng t cắt đường m tại điểm A, đường thẳng t cắt đường n tại điểm B
Góc A1 bằng góc B1
Góc A1 và góc B1 là hai góc đồng vị
- Kết luận: m và n là hai đường thẳng song song
A. Nếu đường thẳng t cắt hai đường thẳng m và n và tạo ra một cặp góc đồng vị bằng nhau, thì hai đường thẳng m và n sẽ vuông góc với nhau;
B. Nếu đường thẳng t cắt hai đường thẳng m và n và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau, thì hai đường thẳng m và n là song song;
C. Nếu đường thẳng t cắt hai đường thẳng m và n và tạo ra một cặp góc so le trong bằng nhau, thì hai đường thẳng m và n là song song;
D. Nếu đường thẳng t cắt hai đường thẳng m và n và tạo ra một cặp góc so le trong bằng nhau, thì hai đường thẳng m và n sẽ vuông góc với nhau.
Hướng dẫn giải
Đáp án chính xác là: B. Nếu một đường thẳng t cắt hai đường thẳng m và n, và tạo thành một cặp góc đồng vị bằng nhau, thì hai đường thẳng m và n là song song với nhau;
Khi một đường thẳng t cắt hai đường thẳng m và n, và tạo ra một cặp góc đồng vị bằng nhau, điều này chứng minh rằng hai đường thẳng m và n là song song.
Bài 6. Định lý sau đây là: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song, thì nó cũng sẽ vuông góc với đường thẳng còn lại”.
Hình minh họa cho định lý này là:
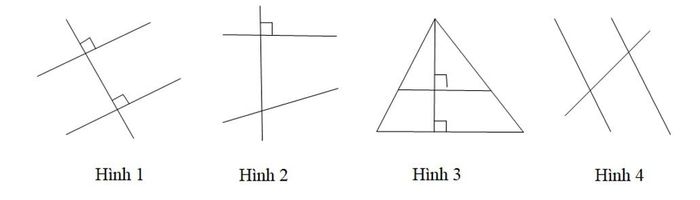
B. Hình 2, Hình 3;
C. Hình 3, Hình 4;
D. Hình 1, Hình 3.
Hướng dẫn giải
Đáp án chính xác là: D. Hình 1 và Hình 3.
Hình 2 không đáp ứng điều kiện về hai đường thẳng song song, vì vậy loại bỏ phương án A và B.
Hình 4 không thỏa mãn điều kiện về việc vuông góc với một trong hai đường thẳng, nên loại phương án C.
Hình 1 và Hình 3 đều đáp ứng đủ hai điều kiện đã nêu.
Do đó, lựa chọn chính xác là phương án D.
Câu 7: Xét hình chóp S.ABCD với đáy là hình bình hành ABCD. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng song song với đường thẳng nào dưới đây?
A. AC B. BD
C. AD D. SC
Hiển thị đáp án
Đáp án chính xác là: C. Giao tuyến của hai mặt phẳng (SAD) và (SBC) song song với đường thẳng AD
Câu 8: Trong hình chóp S.ABCD, với M, N, P, Q lần lượt là trọng tâm của các tam giác SAB, SBC, SCD, SDA. Khẳng định nào dưới đây là chính xác?
A. MNPQ là một hình bình hành.
B. MNPQ là một hình thoi.
C. MNPQ là một hình thang với chỉ một cặp cạnh đối song song.
D. MNPQ là một tứ giác không có cặp cạnh nào song song.
Hiển thị kết quả
Đáp án: A. MNPQ là hình bình hành là khẳng định chính xác
Câu 9: Khi hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song, thì giao tuyến của chúng (nếu có) sẽ:
A. song song với cả hai đường thẳng đó
B. song song với cả hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
C. trùng với một trong hai đường thẳng đó
D. cắt một trong hai đường thẳng đó
Hiển thị kết quả
Đáp án: B. Khi hai mặt phẳng phân biệt chứa hai đường thẳng song song, giao tuyến của chúng (nếu có) sẽ là đường thẳng song song với cả hai đường thẳng đó hoặc trùng với một trong số chúng.
Câu 10: Trong tứ diện ABCD, IJ lần lượt là trung điểm của các cạnh BC và BD. Hãy xác định giao tuyến của hai mặt phẳng (AIJ) và (ACD).
A. Đường thẳng d đi qua A và song song với BC.
B. Đường thẳng d đi qua A và song song với BD.
C. Đường thẳng d đi qua A và song song với CD.
D. Đường thẳng d đi qua A và đi qua M, trong đó M là điểm giao của IJ và CD.
Hiển thị đáp án
Đáp án: C. Đường thẳng d đi qua A và song song với CD.
Câu 11: Trong hình chóp S.ABCD với ABCD là hình bình hành có tâm O, và M, N là các trung điểm của SA và SB. Đoạn giao tuyến của hai mặt phẳng (MNC) và (ABD) là đường nào dưới đây?
A. OA B. OM
C. OC D. CD
Hiển thị đáp án
Đáp án: D. Đoạn giao tuyến của hai mặt phẳng (MNC) và (ABD) là đường CD
Câu 12: Xét tứ diện ABCD, với M và N lần lượt là trọng tâm của tam giác ABC và ABD. Những nhận định nào sau đây là chính xác?
(1) MN song song với mặt phẳng (BCD)
(2) MN song song với mặt phẳng (ACD)
(3) MN song song với mặt phẳng (ABD)
A. Chỉ có (1) đúng B. (2) và (3)
C. (1) và (2) D. (1) và (3)
Đáp án: C. Các khẳng định chính xác là: MN song song với mặt phẳng (BCD) và MN song song với mặt phẳng (ACD).
Câu 13: Trong tứ diện ABCD, giả sử M thuộc đoạn BC. Một mặt phẳng (∝) đi qua M và song song với AB cùng CD. Hình cắt của mặt phẳng (∝) với tứ diện ABCD là hình gì?
A. Hình thang có một cặp cạnh đối song song
B. Hình bình hành
C. Hình tam giác
D. Hình ngũ giác
Đáp án: B. Thiết diện của mặt phẳng (∝) và tứ diện ABCD là hình bình hành.
Giải thích chi tiết:
- Mặt phẳng (∝) song song với AB, do đó giao tuyến của (∝) với mặt phẳng (ABC) sẽ là đường thẳng qua điểm M, song song với AB và cắt AC tại điểm Q.
- Mặt phẳng (∝) song song với CD, vì vậy giao tuyến của (∝) với mặt phẳng (BCD) sẽ là đường thẳng qua điểm N, song song với CD và cắt BD tại điểm N.
Câu 14: Có bao nhiêu cách thức tương tác giữa một đường thẳng và một mặt phẳng?
A. 1 B. 2
C. 3 D. 4
Hiển thị kết quả
Đáp án: C. Có 3 vị trí tương đối giữa một đường thẳng và một mặt phẳng
Câu 15: Xét hai đường thẳng a và b cắt nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?
A. 1 B. 2
C. không D. vô số
Đáp án: A. Chỉ có một mặt phẳng vừa chứa a vừa song song với b
Giải thích chi tiết:
- (∝) song song với AB, do đó giao tuyến của (∝) với (ABD) là đường thẳng đi qua N, song song với AB và cắt AD tại P.
Ta có: MN // PQ // CD, MQ // PN // AB.
Vậy thiết diện là hình bình hành MNPQ. Đáp án là B.
Bài viết từ Mytour hy vọng sẽ cung cấp thông tin hữu ích cho bạn đọc, giúp bạn ôn tập và củng cố kiến thức về đường thẳng song song. Xin chân thành cảm ơn!
