Bài tập về đường tròn trong mặt phẳng tọa độ kèm đáp án chi tiết

Buzz

Nội dung bài viết

1. Bài tập đường tròn trong mặt phẳng tọa độ

2. Đáp án cho bài tập đường tròn trong mặt phẳng tọa độ

3. Ôn tập lý thuyết

Xem thêm

Bài viết dưới đây của Mytour sẽ cung cấp thông tin về 'Bài tập về đường tròn trong mặt phẳng tọa độ với đáp án chi tiết'. Hy vọng bài viết sẽ hỗ trợ bạn ôn tập hiệu quả.

1. Bài tập đường tròn trong mặt phẳng tọa độ

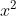
$x^{2} + y^{2} - 4x - 6y + 5 = 0$

A. 2

B. 5

C. 4

D. 7

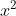
$x^{2} + y^{2} - 4x - 6y + 11 = 0$

A. M(-2; 8)

B. M (9; 2)

C. M (1; 4)

D. M (3; 8)

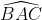
A. B (2; 1)

B. B(2;2)

C. B (2; -1)

D. B (2; -3)

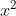
$x^{2} + y^{2} - 4x - 4y - 2 = 0$

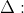
A. (1; 1)

B. (2; 0)

C. (3; -1)

D. (1; 1) hoặc (5; -3)

Câu 5: Cho hai điểm A(8;0) và B (0; 6). Tìm phương trình đường tròn nội tiếp tam giác OAB

$^{2}$ $^{2}$ $^{2}$ $^{2}$ $^{2}$ $^{2}$ $^{2}$ $^{2}$

Câu 6: Trong mặt phẳng tọa độ Oxy, tam giác ABC có hai cạnh AB và AC với phương trình lần lượt là x + y - 2 = 0 và x + 3y - 4 = 0. Cạnh BC có trung điểm M (-1; 1). Xác định tâm của đường tròn ngoại tiếp tam giác ABC.

A. (-5; -7)

B. (4; -3)

C. (-7; 3)

D. (1; 3)

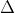
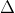
$x^{2} + y^{2} - 4x + 2y - 4 = 0$ $Delta ^{'}$

A. x + y - 2 = 0

B. x + y - 1 = 0

C. x + y = 0

D. x + y + 2 = 0

Câu 8: Xác định phương trình tiếp tuyến d của đường tròn (C): (x -2)² + (y +3)² = 5 tại điểm M (3; -1)

2. Đáp án cho bài tập đường tròn trong mặt phẳng tọa độ

Câu 1:

Lời giải chi tiết

Xét phương trình (C) với y là ẩn và x là tham số

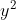
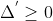
$y^{2}$ $x^{2} - 4x + 5$ $Delta ^{'} geq 0$ $^{2}$

$^{2}$

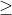
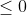
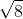
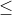
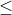
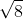
Các điểm M (x; y) nằm trên đường tròn (C) có hoành độ nguyên là 0; 1; 2; 3; 4 là:

x	0	1	2	3	4
y	1 hoặc 5	y không nguyên	y không nguyên	y không nguyên	1 hoặc y = 5

Do đó, có bốn điểm trên (C) có tọa độ nguyên như sau:

(0; 1), (0; 5), (4; 1) và (4; 5)

Do đó, đáp án chính xác là đáp án C

Câu 2:

Giải chi tiết

Đường tròn (C) có tâm tại I (2;3)

Thay tọa độ của điểm A vào phương trình đường tròn, ta có:

$^{2}$ $^{2}$

Điểm A nằm trên đường tròn (C)

Để đoạn MA đạt giá trị lớn nhất, MA phải là đường kính

Điểm M là điểm đối xứng của A qua I, tức I là trung điểm của đoạn MA

Tọa độ của điểm M là:

x = 2.2 - 3 = 1

y = 2.3 - 2 = 4

Do đó, điểm M có tọa độ (1; 4)

Vậy, đáp án chính xác là đáp án C

Câu 3:

Giải chi tiết

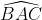
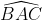^độ

Tam giác BAC vuông tại A, và BC là đường kính

O (0;0) là trung điểm của đoạn BC

Vậy, O(0;0) là trung điểm của BC

Từ đó, n = -2 và m = -1

Do đó, tọa độ của điểm B là (2; -1) và điểm C là (-2; 1)

Do đó, đáp án chính xác là đáp án D

Câu 4:

Giải chi tiết

Đường tròn (C) có tâm tại I(2; -2) và bán kính bằng 3

Chúng ta có nhận xét như sau:

- Nếu điểm A nằm trong hình tròn (C), không thể vẽ tiếp tuyến từ A đến đường tròn

- Nếu điểm A nằm trên đường tròn (C), có thể vẽ chính xác một tiếp tuyến từ A đến đường tròn

- Nếu điểm A nằm ngoài hình tròn (C), có thể vẽ hai tiếp tuyến từ A đến đường tròn

Từ đó, nếu từ điểm A có thể vẽ một tiếp tuyến duy nhất đến đường tròn (C), thì A phải nằm trên đường tròn

Vậy, A là giao điểm giữa đường tròn (C) và đường thẳng d, nên tọa độ của A là nghiệm của hệ phương trình:

$\left\{\begin{matrix} x+ y - 2 & = 0\\ x^{2} + y^{2} - 4x + 4y - 2 = 0 & \end{matrix}\right.$

Giải phương trình sau đây:

$^{2}$ $^{2}$ $^{2}$

Tương ứng: y = 1 nên x = 1

y = -3 nên x = 5

Do đó, đáp án chính xác là đáp án C

Câu 5:

Hướng dẫn giải chi tiết

Chúng ta có:

OA = 8; OB = 6 và AB = 10

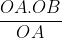
$\frac{1}{2}$ $\frac{OA \cdot OB}{OA + OB + AB}$

Gọi I là tâm của đường tròn nội tiếp tam giác OAB

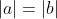
$\left | a \right | = \left | b \right |$

Vì đường tròn có tâm nằm trong góc phần tư thứ nhất nên a > 0, b > 0

Do đó: a = b = r = 2

Vậy tâm của đường tròn nội tiếp tam giác OAB là I(2;2) và bán kính đường tròn nội tiếp là r = 2

Do đó, phương trình của đường tròn nội tiếp tam giác OAB là:

$^{2}$ $^{2}$

Do đó, đáp án chính xác là đáp án A

Câu 6:

Hướng dẫn giải chi tiết

Hai đường thẳng AB và AC giao nhau tại A, do đó tọa độ của điểm A là nghiệm của hệ phương trình:

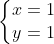
$\left\{\begin{matrix} x + y - 2 = 0 & \\ x + 3y - 4 = 0 & \end{matrix}\right.$ $\left\{\begin{matrix} x = 1 & \\ y = 1 & \end{matrix}\right.$

Vậy tọa độ của điểm A là (1; 1)

Gọi P là trung điểm của đoạn AC. Khi đó, MP // AB (vì MP là đoạn trung bình của tam giác)

Do đó, đường thẳng MP có dạng: x + y + c = 0 với c khác -2

Vì điểm M (-1; 1) nằm trên đường thẳng MP nên: -1 + 1 + c = 0, từ đó c = 0

Phương trình của đường thẳng MP là: x + y = 0

Đoạn MP và AC cắt nhau tại điểm P, với tọa độ P (-2; 2)

Vì P là trung điểm của đoạn AC, nên tọa độ của điểm C là (-5; 3)

Vì điểm M là trung điểm của đoạn BC nên tọa độ của điểm B được tính như sau:

$\left\{\begin{matrix} x = 2 \cdot (-1) + 5 = 3 & \\ y = 2 \cdot 1 - 3 = -1 & \end{matrix}\right.$

Vậy tọa độ của điểm B là (3; -1)

Xây dựng phương trình của đường tròn đi qua ba điểm A, B và C

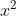
$x^{2} + y^{2} - 2ax - 2by + c = 0$

Vì các điểm A, B, C nằm trên đường tròn nên:

a = -5; b = -7; c = -26

Do đó, phương trình của đường tròn cần tìm có tâm tại I(-5; -7)

Vì vậy, đáp án chính xác là đáp án D

Câu 7:

Hướng dẫn giải chi tiết

Đường tròn (C) có tâm tại I(2; -1) và bán kính R = 3

Để đường thẳng vuông góc và cắt đường tròn tại hai điểm khác nhau với khoảng cách lớn nhất, nó phải vuông góc và đi qua tâm I của đường tròn (C)

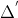
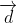
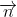
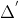
$\Delta ^{'}$ $\overrightarrow{d}$ $\overrightarrow{n}$ $\Delta ^{'}$

hoặc x + y - 1 = 0

Do đó, phương trình của đường thẳng cần tìm là: x + y - 1 = 0

Vậy đáp án chính xác là đáp án B

Câu 8:

Hướng dẫn giải chi tiết

Tính toán: (3 - 2)² + (-1 + 3)² = 5

Vậy điểm M nằm trên đường tròn (C)

Đường tròn (C) có tâm tại I(2; -3)

Phương trình của tiếp tuyến d của đường tròn (C) tại điểm M(3; -1)

-1. (x - 3) + (-2) . (y + 1) = 0

-x - 2y + 1 = 0

Vì vậy, phương trình tiếp tuyến d của đường tròn (C) là -x - 2y + 1 = 0

3. Ôn tập lý thuyết

- Xây dựng phương trình của đường tròn với tâm và bán kính đã cho:

Phương trình của đường tròn có tâm tại I(a; b) và bán kính R được cho bởi:

$^{2}$ $^{2}$ $^{2}$

Ghi chú:

$^{2}$ $^{2}$ $^{2}$ $^{2}$ $^{2}$ $^{2}$ $^{2}$ $^{2}$

- Phương trình tiếp tuyến của một đường tròn là:

Điểm M_o(x_o;y_o) nằm trên đường tròn (C) với tâm I(a;b)

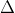Bài tập về đường tròn trong mặt phẳng tọa độ kèm đáp án chi tiết

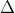
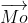
_{(x_o - a) (x - x_o) + (y_o - b)(y - y_o) = 0}

_{Phương trình (1) biểu diễn tiếp tuyến của đường tròn (x - a)² + (y - b)² = R² tại điểm M_o nằm trên đường tròn}

_{Bài viết trên Mytour đã cung cấp thông tin chi tiết về bài tập liên quan đến đường tròn trong mặt phẳng. Cảm ơn bạn đọc đã theo dõi bài viết.}

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]