1. Các lý thuyết cần nắm
1. Khái niệm
- Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại điểm giữa của đoạn thẳng đó
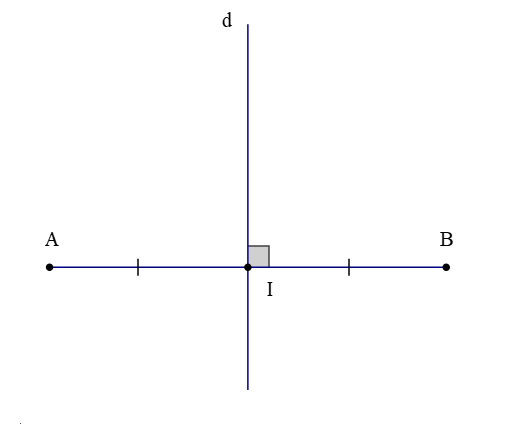
Dựa vào hình vẽ, ta có:
- Đoạn thẳng AB với điểm giữa I của AB
- Đường thẳng d vuông góc với AB tại điểm I
Vì thế, đường thẳng d chính là đường trung trực của AB
Ví dụ:
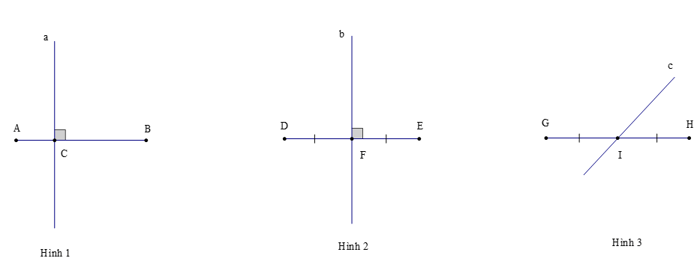
Hướng dẫn giải quyết:
- Quan sát hình 1, ta nhận thấy:
Đường thẳng a vuông góc với AB tại điểm C, nhưng a không đi qua trung điểm của AB
Vì vậy, đường thẳng a không phải là đường trung trực của đoạn thẳng AB
- Nhìn vào hình 2, ta thấy:
Đường thẳng b cắt DE vuông góc tại điểm F và đi qua trung điểm F của đoạn DE
Do đó, b chính là đường trung trực của đoạn DE
- Nhìn vào hình 3, ta nhận thấy:
Đường thẳng c đi qua trung điểm I của đoạn GH nhưng không vuông góc với GH
Vì vậy, đường thẳng c không phải là đường trung trực của đoạn GH
2. Các loại bài tập về đường trung trực của đoạn thẳng
Loại 1: Áp dụng các tính chất của đường trung trực
Sử dụng định lý 1: 'Một điểm nằm trên đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó'
Loại 2: Chứng minh một điểm nằm trên đường trung trực. Chứng minh một đường thẳng là đường trung trực của một đoạn thẳng
- Để chứng minh điểm M nằm trên đường trung trực của đoạn Ab, ta có thể sử dụng định lý 2: 'Một điểm cách đều hai đầu của đoạn thẳng thì thuộc đường trung trực của đoạn đó' hoặc áp dụng định nghĩa về đường trung trực
- Để chứng minh đường thẳng d là đường trung trực của đoạn AB, ta cần chứng minh d chứa hai điểm cách đều A và B hoặc dựa vào định nghĩa đường trung trực
Loại 3: Xác định vị trí của điểm đáp ứng yêu cầu của đề bài
Áp dụng định lý 2: 'Một điểm cách đều hai đầu của đoạn thẳng thì thuộc đường trung trực của đoạn đó' để xác định một điểm nằm trên đường trung trực của đoạn thẳng
Loại 4: Áp dụng tính chất của đường trung trực trong bài toán về cực trị
- Áp dụng tính chất của đường trung trực để điều chỉnh chiều dài một đoạn thẳng sao cho bằng với chiều dài của đoạn thẳng khác
- Sử dụng bất đẳng thức tam giác để xác định giá trị nhỏ nhất và lớn nhất
3. Bài tập ứng dụng
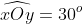
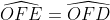

Chi tiết lời giải
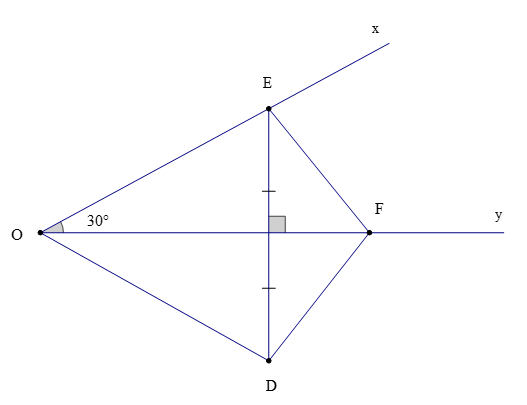
Theo giả thuyết, OF là đường trung trực của ED
Do đó, OE = OD và FE = FD nhờ tính chất của đường trung trực


OE = OD (như đã chứng minh)
FE = FD (như đã chứng minh)
OF là cạnh chung giữa các tam giác


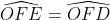
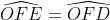
b. Dựa vào phần a, ta có:
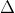

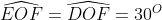


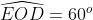


Câu 2: Cho đoạn thẳng AB. Dựng tam giác PAD cân tại P và tam giác QAB cân tại Q như hình minh họa:
.jpg)
Chọn khẳng định chính xác nhất
A. PQ đi qua điểm giữa của đoạn thẳng AB
B. PQ tạo góc vuông với AB
C. PQ không tạo góc vuông với AB
D. PQ là đường trung trực của đoạn thẳng AB
Hướng dẫn giải chi tiết
Đáp án chính xác: D

Do đó, P nằm trên đường trung trực của đoạn thẳng AB (1)

Do đó, Q nằm trên đường trung trực của đoạn thẳng AB (2)
Từ kết quả 1 và 2, ta suy luận rằng PQ chính là đường trung trực của đoạn thẳng AB
Đường trung trực của một đoạn thẳng là đường thẳng vừa đi qua trung điểm của đoạn thẳng vừa vuông góc với đoạn thẳng tại trung điểm đó
Vì vậy, đáp án chính xác là D
Câu 3: Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó thuộc loại nào?
A. Tam giác vuông
B. Tam giác vuông
C. Tam giác đều
D. Tam giác vuông cân
.png)
Giải chi tiết:
Giả sử tam giác ABC có AM là trung tuyến đồng thời là đường trung trực. Chúng ta sẽ chứng minh tam giác ABC là tam giác cân. Vì AM là trung tuyến của tam giác ABC theo giả thiết
Do đó, BM = MC (theo tính chất của trung tuyến)
Vì AM là đường trung trực của BC
Vậy AM vuông góc với BC
Xem xét tam giác vuông ABM và tam giác ACM với các điều kiện sau:
BM = CM như đã chứng minh ở trên
AM: giống nhau


Do đó: AB = AC theo hai cạnh tương ứng

Chọn đáp án chính xác là B
Câu 4: Xét tam giác ABC vuông tại A, với góc C = 30 o và đường trung trực của BC cắt AC tại M. Hãy chọn câu đúng:
A. BM là đường trung tuyến của tam giác ABC
B. BM = AB
C. BM là phân giác của góc ABC
D. BM là đường trung trực của tam giác ABC
.png)
Giải chi tiết:
Vì M nằm trên đường trung trực của BC
Do đó: BM = MC (theo tính chất của điểm nằm trên đường trung trực đoạn thẳng)

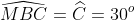
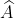
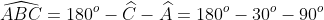 o
o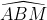
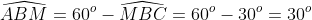
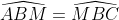
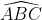
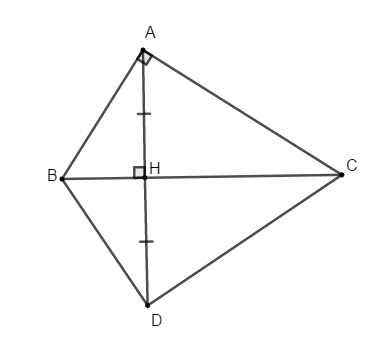
Đáp án chính xác là C
Câu 6: Xét tam giác ABC vuông tại A. Từ điểm A vẽ AH vuông góc với BC tại điểm H. Trên tia đối của HA, chọn điểm D sao cho HA = HD. Khi đó, ta có:
A. Tam giác BCD là tam giác nhọn
B. Tam giác BCD là tam giác vuông tại B
C. Tam giác BCD là tam giác vuông tại D
D. Tam giác BCD là tam giác vuông tại C
Giải chi tiết:
D thuộc tia đối với tia HA, do đó H nằm giữa A và D
Vì HA = HD nên H là điểm chính giữa của AD
Ngoài ra, BC vuông góc với AD tại H (vì AH vuông góc với BC)
Do đó, BC là đường trung trực của đoạn AD
Vậy: BA = BD và CA = CD
Tính chất của điểm nằm trên đường trung trực của đoạn thẳng
Xem xét tam giác ABC và tam giác DBC với các điều kiện sau:
BA = BD và CA = CD như đã chứng minh trước đó
BC: cạnh chung
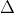

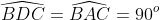
Do đó, tam giác BDC vuông tại D
Đáp án chính xác là C
Câu 7: Xét đoạn thẳng AB. Gọi O là trung điểm của AB. Trong hai nửa mặt phẳng với bờ là đường thẳng AB, chọn hai điểm M và N sao cho MA = MB và NA = NB
A. Đường thẳng MN đi qua O
B. Đường thẳng MN vuông góc với AB
C. Đường thẳng MN vuông góc với AB tại điểm O
D. Đường thẳng MN song song với AB
Giải chi tiết:
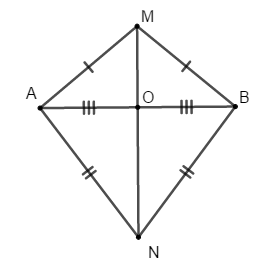
Vì MA = MB nên M nằm trên đường trung trực của đoạn AB
Tương tự, vì NA = NB nên N cũng nằm trên đường trung trực của đoạn AB
Do đó, MN là đường trung trực của đoạn AB
Vì O là trung điểm của AB
Nên MN vuông góc với AB tại O
Đáp án chính xác là đáp án C
Câu 8: Cho đoạn thẳng AB có độ dài 12 cm. I là trung điểm của AB. Điểm M nằm trên đường trung trực của đoạn thẳng AB sao cho MA = 10 cm. Hãy chọn câu sai trong các câu dưới đây:
A. MB = 10 cm
B. MI = 8 cm
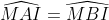
D. MA = MB = MI
I là trung điểm của đoạn thẳng AB
Do đó, IA = IB = 1/2 AB = 1/2 x 12 = 6 cm
Vì M nằm trên đường trung trực của đoạn thẳng AB nên MA = MB = 10 cm
MI là đường trung trực của AB nên nó vuông góc với AB
Do đó, tam giác AMI là tam giác vuông tại I
Áp dụng định lý Pytago, ta có:
MA2 = MI2 + AI2





Kết luận: MI = 8 cm
Chúng ta có: MA = MB và AI = BI
MI: cạnh kề
Vì vậy: Tam giác AMI đồng dạng với tam giác BMI (c.c.c)

Do đó, các điểm A, B, C đúng và D sai vì MA = MB còn MI thì khác
Bài viết trên Mytour đã cung cấp thông tin chi tiết về bài tập liên quan đến đường trung trực của đường thẳng. Cảm ơn các bạn đã theo dõi bài viết này.
