1. Các bài toán nâng cao cho học sinh giỏi lớp 5 kèm đáp án chi tiết
Bài 1: Tìm bốn số tự nhiên có tổng là 2003. Biết rằng nếu loại bỏ chữ số hàng đơn vị của số đầu tiên, ta sẽ được số thứ hai. Nếu tiếp tục loại bỏ chữ số hàng đơn vị của số thứ hai, ta sẽ được số thứ ba. Và nếu loại bỏ chữ số hàng đơn vị của số thứ ba, ta sẽ có số thứ tư.
Đáp án: Số đầu tiên không thể có nhiều hơn 4 chữ số, vì tổng của 4 số chỉ là 2003. Nếu số đầu tiên có ít hơn 4 chữ số, sẽ không đủ để tìm số thứ tư. Do đó, số đầu tiên phải có 4 chữ số.
Gọi số đầu tiên là abcd (a > 0, và a, b, c, d đều nhỏ hơn 10). Các số còn lại lần lượt là: abc ; ab ; a. Dựa vào bài toán, ta có phép tính sau đây:
abcd + abc + ab + a = 2003.
Phân tích số ta có: aaaa + bbb + cc + d = 2003 ()
Từ phép tính () cho thấy a < 2, do đó a = 1. Thay a = 1 vào (*) ta có:
1111 + bbb + cc + d = 2003.
bbb + cc + d = 2003 - 1111
bbb + cc + d = 892 ()
b phải lớn hơn 7, vì nếu b ≤ 7 thì bbb + cc + d sẽ nhỏ hơn 892. Đồng thời, b cũng phải nhỏ hơn 9, vì nếu b = 9 thì bbb = 999, lớn hơn 892. Do đó, b chỉ có thể là 8.
Thay b = 8 vào () ta có:
888 + cc + d = 892
cc + d = 892 - 888
cc + d = 4
Dễ dàng thấy rằng c phải bằng 0 và d là 4.
Do đó, các số là 1804, 180, 18 và 1.
Kiểm tra lại: 1804 + 180 + 18 + 1 = 2003 (đúng)
Bài 2:
Bài giải: Có hai cách để điền dấu cộng:
8 + 7 + 65 + 4 + 3 + 2 + 1 = 90
8 + 7 + 6 + 5 + 43 + 21 = 90
Để tìm ra hai cách này, ta có thể đưa ra nhận xét sau:
Tổng của dãy 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 là 36, vậy 90 - 36 = 54.
Để đạt tổng 90, cần có một hoặc hai số hạng là số hai chữ số. Nếu số đó là 87 hoặc 76 thì không được vì 87 > 54 và 76 > 54. Tuy nhiên, nếu số hai chữ số là 65; 65 + 36 - 6 - 5 = 90, ta có thể sắp xếp như sau:
8 + 7 + 65 + 4 + 3 + 2 + 1 - 90.
Nếu số có hai chữ số là 54 thì cũng không thể đạt tổng 90 vì 54 + 36 - 5 - 4 < 90.
Nếu số có hai chữ số là 43; 43 < 54 nên không phù hợp. Nhưng nếu có hai số hai chữ số là 43 và 21, ta có 43 + 21 - (4 + 3 + 2 + 1) = 54. Do đó, ta có thể viết như sau:
8 + 7 + 6 + 5 + 43 + 21 = 90
Bài 3: S = 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 có phải là một số nguyên không? Giải thích lý do.
Bài giải: Có ba cách giải như sau:
Cách 1: Tính S = 1 201/280
Cách 2: Khi qui đồng mẫu số để tính S, ta có mẫu số chung là số chẵn. Với mẫu số chung này, 1/2; 1/3; 1/4; 1/5; 1/6; 1/7 trở thành các phân số có tử số là số chẵn, chỉ có 1/8 có tử số là số lẻ. Vì vậy, S là phân số có tử số lẻ và mẫu số chẵn, nên S không phải là số nguyên.
Cách 3: Chứng minh rằng 5/4 < S < 2
Thực tế, 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 lớn hơn 6 x 1/8 = 3/4
Do đó, S lớn hơn 3/4 + 1/2 = 5/4
Ngược lại, 1/4 + 1/5 + 1/6 + 1/7 nhỏ hơn 4 x 1/4 = 1
Vì vậy, S nhỏ hơn 1 + 1/2 + 1/3 + 1/8 = 1 + 1/2 + 11/24 nhỏ hơn 2
Vì 5/4 nhỏ hơn S và S nhỏ hơn 2, nên S không phải là số nguyên.
Bài 4: Căn phòng có 4 bức tường, mỗi bức tường treo 3 lá cờ và khoảng cách giữa các lá cờ là đều nhau. Bạn có biết tổng số lá cờ trong phòng là bao nhiêu không?
Bài giải: Để đơn giản, ta sẽ treo tất cả các lá cờ ở cùng một độ cao trên cả 4 bức tường. Khi đó, việc treo cờ giống như bài toán trồng cây. Có 5 cách treo với số lá cờ tương ứng là 8, 9, 10, 11, 12 lá cờ như sau (coi mỗi lá cờ là một điểm chấm tròn):
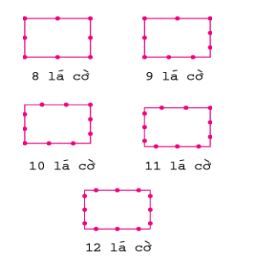
Nếu các lá cờ được treo ở các độ cao khác nhau trên mỗi bức tường, thì 3 lá cờ trên mỗi bức tường sẽ tạo thành 3 đỉnh của một hình tam giác đều. Khi đó, số lá cờ sẽ tương ứng với 6, 7, 8, 9, 10, 11, 12 lá. Dưới đây là 2 cách treo ứng với 6 lá và 7 lá cờ:
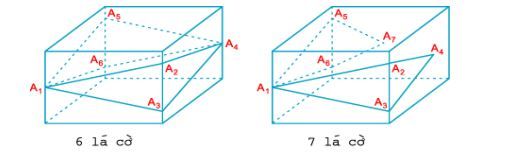
Số lá cờ trong căn phòng có thể dao động từ 6 đến 12 lá.
Bài 5:
Vũ Hữu và Lương Thế Vinh
Hai nhà toán học với cùng một năm sinh
Cả hai đều rất giỏi trong việc thực hành và tính toán
Làm rạng rỡ truyền thống dân tộc của chúng ta
Năm sinh của hai ông là một số bốn chữ số với tổng các chữ số bằng 10. Khi viết năm sinh theo thứ tự ngược lại thì vẫn giữ nguyên năm đó. Bạn đã xác định được năm sinh của hai ông chưa?
Giải: Gọi năm sinh của hai ông là abba (a ≠ 0, a < 3, b <10).
Chúng ta có: a + b + b + a = 10 hay (a + b) x 2 = 10. Vậy a + b = 5.
Vì a ≠ 0 và a < 3 nên a có thể là 1 hoặc 2.
* Nếu a = 1 thì b = 5 - 1 = 4. Như vậy, năm sinh của hai ông là 1441 (đúng).
* Nếu a = 2 thì b = 5 - 2 = 3. Khi đó năm sinh của hai ông là 2332 (không đúng).
Do đó, hai ông Vũ Hữu và Lương Thế Vinh sinh năm 1441.
2. Toán lớp 5 có khó không?
Nhiều bậc phụ huynh hiện nay khá băn khoăn về việc dạy toán lớp 5 cho con cái, và câu hỏi đặt ra là liệu toán lớp 5 có khó không? Câu trả lời là CÓ.
Toán lớp 5 có thể khá thử thách vì đây là giai đoạn chuyển tiếp từ tiểu học lên trung học cơ sở. Bên cạnh các bài tập quen thuộc, còn xuất hiện nhiều kiến thức mới như số thập phân, hình thoi, hình thang, và nhiều hơn nữa. Tuy nhiên, mặc dù toán lớp 5 có vẻ khó, nhưng không phải là không thể vượt qua. Các bạn nhỏ hoàn toàn có thể học tốt môn toán lớp 5 nếu bắt đầu từ đầu với sự nghiêm túc và áp dụng những phương pháp học tập hiệu quả được đề cập dưới đây:
(1) Chuẩn bị bài trước khi đến lớp: Trước khi đến lớp, các con nên dành thời gian ôn lại bài cũ và tìm hiểu kiến thức mới. Chỉ cần 10 - 15 phút để xem qua bài học, các bạn nhỏ có thể củng cố kiến thức và hiểu nội dung bài học sắp tới. Nếu gặp phần nào chưa rõ, các con nên đánh dấu và nhờ thầy cô giải thích khi đến lớp.
(2) Chú ý trong giờ học: Lời giảng của thầy cô là rất quan trọng. Bố mẹ cần giúp con rèn luyện khả năng tập trung khi nghe giảng. Kiến thức toán lớp 5 khá phức tạp và quan trọng, vì vậy việc bỏ lỡ bất kỳ phần nào có thể gây ra lỗ hổng trong kiến thức của các con.
(3) Tích cực làm bài tập: Các con cần hoàn thành tất cả bài tập được giao về nhà một cách nghiêm túc. Việc tiếp xúc với nhiều dạng bài tập sẽ giúp các em rèn luyện tư duy và phản xạ. Nếu chưa tự tin, hãy bắt đầu với các bài dễ trước để nắm vững kiến thức cơ bản. Sau khi đã làm quen với các bài dễ, hãy chuyển sang bài khó hơn để nâng cao khả năng. Nếu hoàn thành được cả ba giai đoạn này, các em sẽ trở thành “bậc thầy” trong việc giải toán, khó có bài nào làm khó được các em sau khi đã chinh phục tất cả các bài tập đó.
