

Mã đi tuần hay hành trình quân mã là bài toán liên quan đến việc di chuyển quân mã trên bàn cờ vua (8 x 8). Quân mã bắt đầu từ một ô trống và cần di chuyển theo quy tắc cờ vua để đi qua tất cả các ô của bàn cờ chỉ một lần.
Có tới 26.534.728.821.064 cách giải bài toán này, trong đó quân mã có thể kết thúc tại ô khởi đầu của nó.
Một hành trình được gọi là hành trình đóng nếu quân mã có thể quay trở lại ô xuất phát sau khi đi qua tất cả 64 ô của bàn cờ. Nếu không thể trở về ô xuất phát bằng một nước đi từ ô cuối, thì đó là hành trình mở.
Chủ đề này đã được các nhà toán học, bao gồm cả Euler, nghiên cứu với nhiều biến thể, chẳng hạn như:
- Thay đổi kích thước của bàn cờ
- Chuyển đổi thành trò chơi hai người
- Giảm bớt yêu cầu về đường đi của quân mã
Bài toán mã đi tuần là một dạng của bài toán tổng quát hơn về tìm đường đi Hamilton trong lý thuyết đồ thị, một bài toán NP-đầy đủ. Việc tìm hành trình đóng của quân mã là một dạng cụ thể của bài toán tìm chu trình Hamilton.
Hành trình của quân mã trên nửa bàn cờ đã được miêu tả dưới dạng thơ trong một tác phẩm tiếng Phạn.
Giải thuật đầu tiên hoàn chỉnh cho bài toán hành trình của quân mã là Giải thuật Warnsdorff, được giới thiệu lần đầu vào năm 1823 bởi H. C. Warnsdorff.
Định lý Schwenk
Trên bàn cờ m × n bất kỳ với m ≤ n, không thể có hành trình đóng của quân mã nếu một trong các điều kiện sau đây được thỏa mãn:
- m và n đều là số lẻ
- m = 1, 2, hoặc 4 và n khác 1
- m = 3 và n là 4, 6, hoặc 8
Điều kiện 1
Khi điều kiện 1 được đáp ứng, dễ dàng chứng minh rằng không tồn tại hành trình đóng của quân mã.
Trên bàn cờ vua, các ô đen và trắng luân phiên nhau, và quân mã chỉ di chuyển từ ô này sang ô khác màu.
Khi m và n đều là số lẻ, số ô đen và trắng trên bàn cờ không bằng nhau. Ví dụ, trên bàn cờ 5×5 có 13 ô đen và 12 ô trắng.
Để có một hành trình đóng, số ô đen và trắng phải bằng nhau, do đó tổng số ô của bàn cờ phải là số chẵn. Vì vậy, không thể có hành trình đóng khi số ô trên bàn cờ là số lẻ.
Điều kiện 2
Khi độ dài cạnh nhỏ nhất là 1, 2, hoặc 4, không thể tồn tại hành trình đóng của quân mã.
Dễ dàng nhận thấy rằng khi m = 1 hoặc 2, quân mã không thể hoàn thành hành trình: quân mã không thể đi qua tất cả các ô (trừ trường hợp bàn cờ 1x1).
Bàn cờ kích thước 4 × n không thể có hành trình đóng của quân mã.
Giả sử có một hành trình đóng của quân mã trên bàn cờ kích thước 4 × n. Ta chia bàn cờ thành hai tập hợp các ô: gồm các ô đen và gồm các ô trắng. Quân mã luôn di chuyển từ ô đen sang ô trắng và ngược lại, theo quy tắc cờ vua.
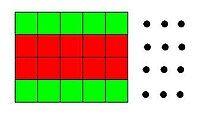
.
Xem xét hình minh họa bên phải. Định nghĩa là tập hợp các ô màu xanh lá cây và là tập hợp các ô màu đỏ trong hình. Các tập này có số ô bằng nhau. Lưu ý rằng từ một ô thuộc , quân mã chỉ có thể nhảy đến ô thuộc . Ngược lại, từ một ô thuộc , quân mã phải nhảy về một ô thuộc . Nếu không, quân mã sẽ có hai ô liên tiếp trong , điều này không xảy ra.
Chúng ta sẽ thấy một mâu thuẫn trong lập luận sau.
Giả sử tồn tại một hành trình đóng của quân mã, ta có thể chọn bất kỳ ô nào làm ô khởi đầu.
- Chọn ô đầu tiên thuộc tập .
- Ô thứ hai sẽ thuộc .
- Ô thứ ba thuộc tập .
- Ô thứ tư thuộc tập .
- ...
Vì vậy, hành trình này không bao gồm các ô thuộc và , do đó không thể bao phủ tất cả các ô trên bàn cờ.
Điều kiện 3
Điều kiện 3 được chứng minh cho từng trường hợp cụ thể. Tuy nhiên, vẫn có thể tìm được lời giải cho hành trình mở. Ví dụ, trên bàn cờ 3 × 4, có 4 hành trình mở khả thi.
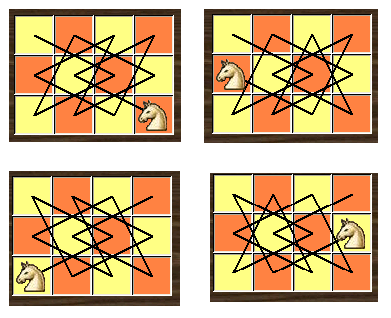
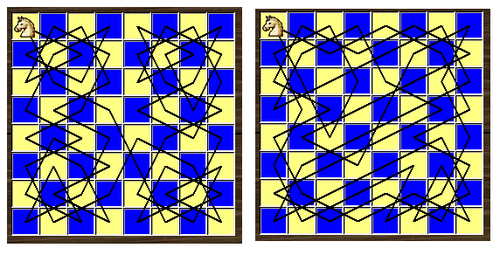
Hai ví dụ về lời giải trên bàn cờ 8 × 8
- Bài toán tám quân hậu
- Quân mã trong cờ vua
- Chú thích
- Nguồn tài liệu
- Watkins, John J. Across the Board: the Mathematics of Chessboard Problems. Princeton UP, 2004.
Liên kết tham khảo
- Trang tổng hợp các liên kết về bài toán hành trình của quân mã Lưu trữ ngày 2004-08-06 trên Wayback Machine
- Bài toán hành trình quân mã Lưu trữ ngày 2018-06-29 trên Wayback Machine
- Ghi chú về hành trình quân mã
- Triển khai thuật toán quay lui đơn giản bằng C++ Lưu trữ ngày 2013-11-14 trên Wayback Machine
- Số lượng hành trình quân mã trên bàn cờ 2n X 2n Chuỗi số nguyên Sloane A001230
- Chiến lược hành trình quân mã trên bàn cờ 8x8
- Hành trình quân mã 8x8 có thể chơi được
