Key takeaways |
|---|
Để giải bài toán về mối quan hệ tuyến tính, người học cần thực hiện lần lượt các bước sau:
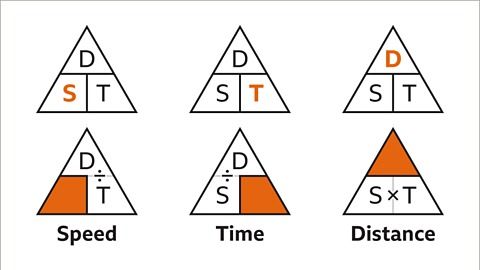
Công thức cần nhớ cho bài toán chuyển động với vận tốc không đổi của các phương tiện:
|
Khái quát về dạng bài Linear relationship word problems
Bài toán về mối quan hệ tuyến tính liên quan đến những bài toán thực tế trong đó hai biến có mối quan hệ tỷ lệ và được biểu diễn bằng một đường thẳng khi biểu diễn trên đồ thị hệ trục toạ độ Oxy.
Trong các bài toán này, những thay đổi trong một biến sẽ dẫn đến sự thay nhất quán của biến còn lại. Mục tiêu của những bài toán này là đưa vấn đề thành một phương trình toán học có dạng y = ax + b, trong đó:
y là biến phụ thuộc
x là biến độc lập
a: hệ số góc
b là giao điểm của đường thẳng y = ax + b với trục Oy khi x = 0
Những bài toán về mối quan hệ tuyến tính thường liên quan đến các tình huống như tính toán chi phí dựa trên tỷ lệ cố định, xác định khoảng cách dựa trên tốc độ và thời gian hoặc tìm tổng số tiền khi cộng các số lượng nhất quán.
Phương pháp giải bài dạng Linear relationship word problems trong SAT Toán
Đọc kỹ đề bài để xác định yêu cầu cũng như các thông tin được cho sẵn
Chọn biến đại diện phù hợp đại diện cho các đại lượng trong bài toán và đặt điều kiện cho biến. Tìm sự liên hệ của các biến, chú ý đến các cụm từ như “per”, “each”, “every”, … để xác định hệ số góc
Viết phương trình biểu thị mối liên hệ giữa các biến dưới dạng y = ax + b
Giải phương trình dựa vào các tính chất đã học
Kiểm tra điều kiện nghiệm của phương trình rồi kết luận.
Ví dụ 1: Sarah is driving to her friend’s house, which is 120 miles away. She drives at a constant speed of 60 miles per hour. Write an equation that can be used to find t, the number of hours it will take Sarah to reach her friend’s house, and determine how long it will take her to complete the trip.
(Sarah lái xe tới nhà bạn cách nhà mình 120 dặm. Cô ấy lái xe với vận tốc không đổi là 60 dặm trên giờ. Viết phương trình tìm t - số giờ mà Sarah cần để đến nhà bạn, và xác định Sarah mất bao nhiêu giờ để hoàn thành chuyến đi.)
1. The problem asks for the equation of t, and value of t
2. t is the time that it takes Sarah to drive to her friend’s house (t > 0)
3. Distance = Speed × time
⇒ 120 = 60t
4. 120 = 60t
⇔ t = 2
5. It takes Sarah 2 hours to drive to her friend’s house.
Dịch nghĩa:
1. Đề bài yêu cầu viết phương trình tìm t và tìm giá trị của t
2. t là số giờ mà Sarah cần để lái xe đến nhà bạn (t > 0)
3. Quãng đường = Vận tốc × Thời gian
⇒ 120 = 60t
4. 120 = 60t
⇔ t = 2
5. Sarah cần 2 tiếng để lái xe từ nhà mình đến nhà bạn.
Ví dụ 2: The temperature in a room is initially 68°F. The room's temperature is expected to increase by 2°F every hour as the heater is turned on. Write an equation to represent the temperature T in the room after h hours, and use it to determine how many hours it will take for the temperature to reach 80°F.
(Nhiệt độ của căn phòng ban đầu là 68°F. Nhiệt độ của phòng được dự đoán sẽ tăng 2°F mỗi giờ khi máy sưởi được bật. Viết phương trình thể hiện nhiệt độ T trong phòng sau h giờ, và xác định sau bao lâu thì nhiệt độ căn phòng đạt 80°F.)
1. The problem asks for the equation to represent the temperature of T and calculate h if T = 80°F
2. T is the temperature of the room after h hours
3. The initial temperature in a room is 68°F, and increases 2°F each hour, then the temperature in the room after T hours is:
T = 68 + 2h
4. With T = 80:
⇔ 80 = 68 + 2h
⇔ 2h = 12
⇔ h = 6
5. The equation to calculate T after h hours is T = 68 + 2h and it takes 6 hours to increase the temperature in the room from 68°F to 80°F.
(dịch)
1. Bài toán yêu cầu xác định phương trình tìm nhiệt độ T và tính h khi T = 80°F
2. T là nhiệt độ phòng sau h giờ.
3. Nhiệt độ ban đầu của phòng là = 68°F, và tăng 2°F sau mỗi giờ, vậy nhiệt độ phòng T sau h giờ là
T = 68 + 2h
4. Với T = 80,
⇔ 80 = 68 + 2h
⇔ 2h = 12
⇔ h = 6
5. Phương trình tính nhiệt độ T sau h giờ là T = 68 + 2h và mất 6 giờ để căn phòng tăng nhiệt độ từ 68°F lên 80°F.
Một số điểm cần chú ý
Distance (d) = Speed × Time (Khoảng cách = Vận tốc × Thời gian)
Speed = Distance/ Time (Vận tốc = Khoảng cách/Thời gian)
Time = Distance / Speed (Thời gian = Khoảng cách/Vận tốc)
Bài tập thực hành
Bài 2: Maria's current salary is $40,000 per year. She receives an annual raise of $2,000. Write an equation to find t, the number of years it will take for Maria's salary to reach $50,000.
Bài 3: John starts jogging at a park that is 2 miles away from his home. He jogs away from his home at a constant speed of 4 miles per hour. Write an equation to find d, the number of hours it takes John to be 10 miles away from his home.
Giải đáp
Equation: 130 = 8x + 50
Solve for x: x = 10 minutes
Bài 2:
Equation: 50,000 = 2,000t + 40,000
Solve for t: t = 5 years
Bài 3
Equation: 10 = 4t + 2
Giải t = 2 giờ
Tổng kết lại
Tài liệu tham khảo
'SAT Math: Tổng hợp các dạng bài toán phổ biến trong đề SAT.' https://americanstudy.edu.vn/, americanstudy.edu.vn/sat-math-tong-hop-cac-dang-toan-pho-bien-trong-de-sat/.
Khan Academy | Khóa học và bài tập trực tuyến miễn phí, www.khanacademy.org/test-prep/v2-sat-math/x0fcc98a58ba3bea7/x0fcc98a58ba3bea7/a/v2-sat-lesson-understanding-linear-relationships.
